
HL Paper 2
Consider the following reaction studied at 263 K.
\[{\text{2NO(g)}} + {\text{C}}{{\text{l}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2NOCl(g)}}\]
It was found that the forward reaction is first order with respect to \({\rm{C}}{{\rm{l}}_2}\) and second order with respect to NO. The reverse reaction is second order with respect to NOCl.
Consider the following equilibrium reaction.
\[\begin{array}{*{20}{c}} {{\text{C}}{{\text{l}}_2}({\text{g)}} + {\text{S}}{{\text{O}}_2}({\text{g)}} \rightleftharpoons {\text{S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}({\text{g)}}}&{\Delta {H^\Theta } = - 84.5{\text{ kJ}}} \end{array}\]
In a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) closed container, at 375 °C, \({\text{8.60}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ mol}}\) of \({\text{S}}{{\text{O}}_{\text{2}}}\) and \({\text{8.60}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ mol}}\) of \({\text{C}}{{\text{l}}_{\text{2}}}\) were introduced. At equilibrium, \({\text{7.65}} \times {\text{1}}{{\text{0}}^{ - 4}}{\text{ mol}}\) of \({\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\) was formed.
State the rate expression for the forward reaction.
Predict the effect on the rate of the forward reaction and on the rate constant if the concentration of NO is halved.
1.0 mol of \({\rm{C}}{{\rm{l}}_2}\) and 1.0 mol of NO are mixed in a closed container at constant temperature. Sketch a graph to show how the concentration of NO and NOCl change with time until after equilibrium has been reached. Identify the point on the graph where equilibrium is established.
Consider the following reaction.
\[{\text{N}}{{\text{O}}_2}{\text{(g)}} + {\text{CO(g)}} \to {\text{NO(g)}} + {\text{C}}{{\text{O}}_2}{\text{(g)}}\]
Possible reaction mechanisms are:
\(\begin{array}{*{20}{l}} {{\text{Above 775 K:}}}&{{\text{N}}{{\text{O}}_2} + {\text{CO}} \to {\text{NO}} + {\text{C}}{{\text{O}}_{\text{2}}}}&{{\text{slow}}} \\ {{\text{Below 775 K:}}}&{{\text{2N}}{{\text{O}}_2} \to {\text{NO}} + {\text{N}}{{\text{O}}_{\text{3}}}}&{{\text{slow}}} \\ {}&{{\text{N}}{{\text{O}}_3} + {\text{CO}} \to {\text{N}}{{\text{O}}_2} + {\text{C}}{{\text{O}}_2}}&{{\text{fast}}} \end{array}\)
Based on the mechanisms, deduce the rate expressions above and below 775 K.
State two situations when the rate of a chemical reaction is equal to the rate constant.
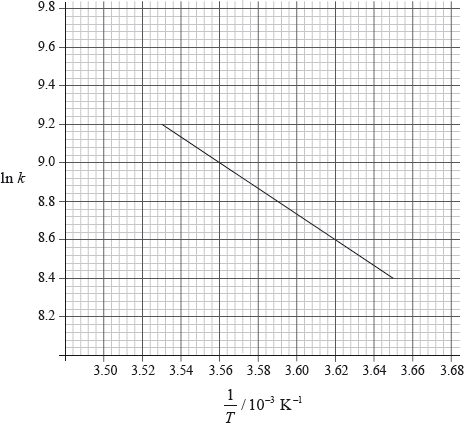
Consider the following graph of \(\ln k\) against \(\frac{1}{T}\) for the first order decomposition of \({{\text{N}}_{\text{2}}}{{\text{O}}_{\text{4}}}\) into \({\text{N}}{{\text{O}}_{\text{2}}}\). Determine the activation energy in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\) for this reaction.
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction.
Determine the value of the equilibrium constant, \({K_{\text{c}}}\).
If the temperature of the reaction is changed to 300 °C, predict, stating a reason in each case, whether the equilibrium concentration of \({\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\) and the value of \({K_{\text{c}}}\) will increase or decrease.
If the volume of the container is changed to \({\text{1.50 d}}{{\text{m}}^{\text{3}}}\), predict, stating a reason in each case, how this will affect the equilibrium concentration of \({\text{S}}{{\text{O}}_2}{\text{C}}{{\text{l}}_2}\) and the value of \({K_{\text{c}}}\).
Suggest, stating a reason, how the addition of a catalyst at constant pressure and temperature will affect the equilibrium concentration of \({\text{S}}{{\text{O}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{2}}}\).
A class studied the equilibrium established when ethanoic acid and ethanol react together in the presence of a strong acid, using propanone as an inert solvent. The equation is given below.
\[{\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH}} + {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}{\text{OH}} \rightleftharpoons {\text{C}}{{\text{H}}_{\text{3}}}{\text{COO}}{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}} + {{\text{H}}_{\text{2}}}{\text{O}}\]
One group made the following initial mixture:
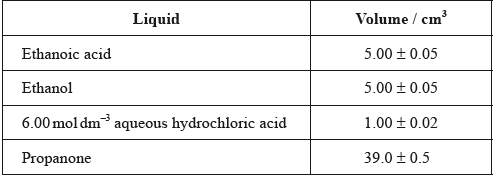
After one week, a \(5.00 \pm 0.05{\text{ c}}{{\text{m}}^{\text{3}}}\) sample of the final equilibrium mixture was pipetted out and titrated with \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous sodium hydroxide to determine the amount of ethanoic acid remaining. The following titration results were obtained:
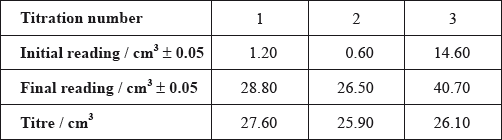
The density of ethanoic acid is \({\text{1.05 g}}\,{\text{c}}{{\text{m}}^{ - 3}}\). Determine the amount, in mol, of ethanoic acid present in the initial mixture.
The concentration of ethanoic acid can be calculated as \({\text{1.748 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Determine the percentage uncertainty of this value. (Neglect any uncertainty in the density and the molar mass.)
Calculate the absolute uncertainty of the titre for Titration 1 (\({\text{27.60 c}}{{\text{m}}^3}\)).
Suggest the average volume of alkali, required to neutralize the \({\text{5.00 c}}{{\text{m}}^{\text{3}}}\) sample, that the student should use.
\({\text{3.00 c}}{{\text{m}}^{\text{3}}}\) of the \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous sodium hydroxide reacted with the hydrochloric acid present in the \({\text{5.00 c}}{{\text{m}}^{\text{3}}}\) sample. Determine the concentration of ethanoic acid in the final equilibrium mixture.
Deduce the equilibrium constant expression for the reaction.
The other concentrations in the equilibrium mixture were calculated as follows:

Use these data, along with your answer to part (iii), to determine the value of the equilibrium constant. (If you did not obtain an answer to part (iii), assume the concentrations of ethanol and ethanoic acid are equal, although this is not the case.)
Outline how you could establish that the system had reached equilibrium at the end of one week.
Outline why changing the temperature has only a very small effect on the value of the equilibrium constant for this equilibrium.
Outline how adding some ethyl ethanoate to the initial mixture would affect the amount of ethanoic acid converted to product.
Propanone is used as the solvent because one compound involved in the equilibrium is insoluble in water. Identify this compound and explain why it is insoluble in water.
Suggest one other reason why using water as a solvent would make the experiment less successful.
A mixture of 1.00 mol SO2(g), 2.00 mol O2(g) and 1.00 mol SO3(g) is placed in a 1.00 dm3 container and allowed to reach equilibrium.
2SO2(g) + O2(g) \( \rightleftharpoons \) 2SO3(g)
Nitrogen oxide is in equilibrium with dinitrogen dioxide.
2NO(g) \( \rightleftharpoons \) N2O2(g) ΔHΘ < 0
Deduce, giving a reason, the effect of increasing the temperature on the concentration of N2O2.
A two-step mechanism is proposed for the formation of NO2(g) from NO(g) that involves an exothermic equilibrium process.
First step: 2NO(g) \( \rightleftharpoons \) N2O2(g) fast
Second step: N2O2(g) + O2 (g) → 2NO2(g) slow
Deduce the rate expression for the mechanism.
The rate constant for a reaction doubles when the temperature is increased from 25.0 °C to 35 °C.
Calculate the activation energy, Ea, in kJ mol−1 for the reaction using section 1 and 2 of the data booklet.
In an experiment conducted at 25.0 °C, the initial concentration of propanoic acid and methanol were \({\text{1.6 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) and \({\text{2.0 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) respectively. Once equilibrium was established, a sample of the mixture was removed and analysed. It was found to contain \({\text{0.80 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) of compound X.
Two compounds, A and D, each have the formula \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{9}}}{\text{Cl}}\).
Compound A is reacted with dilute aqueous sodium hydroxide to produce compound B with a formula of \({{\text{C}}_{\text{4}}}{{\text{H}}_{{\text{10}}}}{\text{O}}\). Compound B is then oxidized with acidified potassium
manganate(VII) to produce compound C with a formula of \({{\text{C}}_{\text{4}}}{{\text{H}}_{\text{8}}}{\text{O}}\). Compound C resists further oxidation by acidified potassium manganate(VII).
Compound D is reacted with dilute aqueous sodium hydroxide to produce compound E with a formula of \({{\text{C}}_{\text{4}}}{{\text{H}}_{{\text{10}}}}{\text{O}}\). Compound E does not react with acidified potassium manganate(VII).
Deduce the structural formulas for compounds A, B, C, D and E.
A:
B:
C:
D:
E:
Deduce an equation for the reaction between propanoic acid and methanol. Identify the catalyst and state the name of the organic compound, X, formed.
Calculate the concentrations of the other three species present at equilibrium.
State the equilibrium constant expression, \({K_{\text{c}}}\), and calculate the equilibrium constant for this reaction at 25.0 °C.
2-chloro-3-methylbutane reacts with sodium hydroxide via an \({{\text{S}}_{\text{N}}}{\text{2}}\) mechanism. Explain the mechanism by using curly arrows to represent the movement of electron pairs.
Explain why the hydroxide ion is a better nucleophile than water.
1-chlorobutane can be converted to a pentylamine via a two stage process. Deduce equations for each step of this conversion including any catalyst required and name the organic product produced at each stage.
Bonds can be formed in many ways.
Bonds can be formed in many ways.
The equilibrium for a mixture of NO2 and N2O4 gases is represented as:
2NO2(g) \( \rightleftharpoons \) N2O4(g)
At 100°C, the equilibrium constant, Kc, is 0.21.
Discuss the bonding in the resonance structures of ozone.
Deduce one resonance structure of ozone and the corresponding formal charges on each oxygen atom.
The first six ionization energies, in kJ mol–1, of an element are given below.

Explain the large increase in ionization energy from IE3 to IE4.
At a given time, the concentration of NO2(g) and N2O4(g) were 0.52 and \(0.10{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) respectively.
Deduce, showing your reasoning, if the forward or the reverse reaction is favoured at this time.
Comment on the value of ΔG when the reaction quotient equals the equilibrium constant, Q = K.
Many reactions are in a state of equilibrium.
The following reaction was allowed to reach equilibrium at 761 K.
H2 (g) + I2 (g) \( \rightleftharpoons \) 2HI (g) ΔHθ < 0
The pH of 0.010 mol dm–3 carbonic acid, H2CO3 (aq), is 4.17 at 25 °C.
H2CO3 (aq) + H2O (l) \( \rightleftharpoons \) HCO3– (aq) + H3O+ (aq).
State the equilibrium constant expression, Kc , for this reaction.
The following equilibrium concentrations in mol dm–3 were obtained at 761 K.
Calculate the value of the equilibrium constant at 761 K.
Determine the value of ΔGθ, in kJ, for the above reaction at 761 K using section 1 of the data booklet.
Calculate [H3O+] in the solution and the dissociation constant, Ka , of the acid at 25 °C.
Calculate Kb for HCO3– acting as a base.
When nitrogen gas and hydrogen gas are allowed to react in a closed container the following equilibrium is established.
\[{{\text{N}}_{\text{2}}}{\text{(g)}} + {\text{3}}{{\text{H}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_{\text{3}}}{\text{(g) }}\Delta H = -92.6{\text{ kJ}}\]
Outline two characteristics of a reversible reaction in a state of dynamic equilibrium.
Predict, with a reason, how each of the following changes affects the position of equilibrium.
The volume of the container is increased.
Ammonia is removed from the equilibrium mixture.
Define the term activation energy, \({E_{\text{a}}}\).
Ammonia is manufactured by the Haber process in which iron is used as a catalyst.
Explain the effect of a catalyst on the rate of reaction.
Typical conditions used in the Haber process are 500 °C and 200 atm, resulting in approximately 15% yield of ammonia.
(i) Explain why a temperature lower than 500 °C is not used.
(ii) Outline why a pressure higher than 200 atm is not often used.
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction on page 10.
When 1.00 mol of nitrogen and 3.00 mol of hydrogen were allowed to reach equilibrium in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container at a temperature of 500 °C and a pressure of 1000 atm, the equilibrium mixture contained 1.46 mol of ammonia.
Calculate the value of \({K_{\text{c}}}\) at 500 °C.
Define the term base according to the Lewis theory.
Define the term weak base according to the Brønsted–Lowry theory.
Deduce the formulas of conjugate acid-base pairs in the reaction below.
\[{\text{C}}{{\text{H}}_{\text{3}}}{\text{N}}{{\text{H}}_{\text{2}}}{\text{(aq)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}} \rightleftharpoons {\text{C}}{{\text{H}}_{\text{3}}}{\text{NH}}_{\text{3}}^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]
Determine the pH of a \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\), using tables 2 and 15 of the data booklet.
(i) Sketch the pH titration curve obtained when \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\) is added to \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{HCl (aq)}}\).
(ii) Identify an indicator from table 16 of the data booklet that could be used for this titration.
The Haber process enables the large-scale production of ammonia needed to make fertilizers.
The equation for the Haber process is given below.
\[{{\text{N}}_2}({\text{g)}} + 3{{\text{H}}_2}({\text{g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_3}({\text{g)}}\]
The percentage of ammonia in the equilibrium mixture varies with temperature.
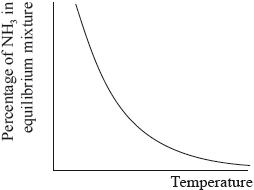
Ammonia can be converted into nitric acid, \({\text{HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\), and hydrocyanic acid, HCN(aq). The \({\text{p}}{K_{\text{a}}}\) of hydrocyanic acid is 9.21.
A student decided to investigate the reactions of the two acids with separate samples of \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.
(i) Use the graph to deduce whether the forward reaction is exothermic or endothermic and explain your choice.
(ii) State and explain the effect of increasing the pressure on the yield of ammonia.
(iii) Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction.
(iv) A mixture of 1.00 mol \({{\text{N}}_{\text{2}}}\) and 3.00 mol \({{\text{H}}_{\text{2}}}\) was placed in a \({\text{1.0 d}}{{\text{m}}^{\text{3}}}\) flask at 400 °C. When the system was allowed to reach equilibrium, the concentration of was found to be \({\text{0.062 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Determine the equilibrium constant, \({K_{\text{c}}}\), of the reaction at this temperature.
(v) Iron is used as a catalyst in the Haber process. State the effect of a catalyst on the value of \({K_{\text{c}}}\).
(i) Distinguish between the terms strong and weak acid and state the equations used to show the dissociation of each acid in aqueous solution.
(ii) Deduce the expression for the ionization constant, \({K_{\text{a}}}\), of hydrocyanic acid and calculate its value from the \({\text{p}}{K_{\text{a}}}\) value given.
(iii) Use your answer from part (b) (ii) to calculate the \({\text{[}}{{\text{H}}^ + }{\text{]}}\) and the pH of an aqueous solution of hydrocyanic acid of concentration \({\text{0.108 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). State one assumption made in arriving at your answer.
A small piece of magnesium ribbon is added to solutions of nitric and hydrocyanic acid of the same concentration at the same temperature. Describe two observations that would allow you to distinguish between the two acids.
(i) Calculate the volume of the sodium hydroxide solution required to react exactly with a \({\text{15.0 c}}{{\text{m}}^{\text{3}}}\) solution of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) nitric acid.
(ii) The following hypothesis was suggested by the student: “Since hydrocyanic acid is a weak acid it will react with a smaller volume of the \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.” Comment on whether or not this is a valid hypothesis.
(iii) Use Table 16 of the Data Booklet to identify a suitable indicator for the titration of sodium hydroxide and hydrocyanic acid.
An equilibrium exists between nitrosyl chloride, NOCl, nitrogen oxide, NO, and chlorine, \({\text{C}}{{\text{l}}_{\text{2}}}\).
\[{\text{2NOCl(g)}} \rightleftharpoons {\text{2NO(g)}} + {\text{C}}{{\text{l}}_2}{\text{(g)}}\]
\({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of hexane, \({{\text{C}}_{\text{6}}}{{\text{H}}_{{\text{14}}}}\), and \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of pentan-1-ol, \({{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{11}}}}{\text{OH}}\), were placed separately into two closed containers at 298 K and allowed to reach equilibrium.
Ammonia is a weak base.
(i) Deduce the equilibrium constant expression for this reaction.
(ii) Explain the effect on the position of equilibrium and the value of \({K_{\text{c}}}\) when pressure is decreased and temperature is kept constant.
(iii) 2.00 mol of NOCl was placed in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container and allowed to reach equilibrium at 298 K. At equilibrium, 0.200 mol of NO was present. Determine the equilibrium concentrations of NOCl and \({\text{C}}{{\text{l}}_{\text{2}}}\), and hence calculate the value of \({K_{\text{c}}}\) at this temperature.
(iv) The value of \({K_{\text{c}}}\) is \(1.60 \times {10^{ - 5}}\) at 318 K. State and explain whether the forward reaction is exothermic or endothermic.
(i) Compare the two liquids in terms of their boiling points, enthalpies of vaporization and vapour pressures.
(ii) Explain your answer given for part (b)(i).
Calculate the pH of a \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia at 298 K to two decimal places, using Table 15 of the Data Booklet.
A buffer solution is made using \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid, HCl (aq), and \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\).
Describe the meaning of the term buffer solution.
Determine the pH of the buffer solution at 298 K.
A \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia is added to \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of a \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid solution in a titration experiment.
Calculate the total volume of the solution at the equivalence point.
Calculate the pH of the solution at the equivalence point, using Table 15 of the Data Booklet.
Identify a suitable indicator for this titration, using Table 16 of the Data Booklet.
The rate of reaction is an important factor in industrial processes such as the Contact process to make sulfur trioxide, \({\text{S}}{{\text{O}}_{\text{3}}}{\text{(g)}}\).
Define the term rate of reaction.
Describe the collision theory.
The Contact process involves this homogeneous equilibrium:
\[{\text{2S}}{{\text{O}}_{\text{2}}}{\text{(g)}} + {{\text{O}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2S}}{{\text{O}}_{\text{3}}}{\text{(g)}}\,\,\,\,\,\Delta H = - 198{\text{ kJ}}\]
State and explain how increasing the pressure of the reaction mixture affects the yield of \({\text{S}}{{\text{O}}_{\text{3}}}\).
The Contact process involves this homogeneous equilibrium:
\[{\text{2S}}{{\text{O}}_{\text{2}}}{\text{(g)}} + {{\text{O}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2S}}{{\text{O}}_{\text{3}}}{\text{(g)}}\,\,\,\,\,\Delta H = - 198{\text{ kJ}}\]
2.00 mol of \({\text{S}}{{\text{O}}_{\text{2}}}{\text{(g)}}\) are mixed with 3.00 mol of \({{\text{O}}_{\text{2}}}{\text{(g)}}\) in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container until equilibrium is reached. At equilibrium there are 0.80 mol of \({\text{S}}{{\text{O}}_{\text{3}}}{\text{(g)}}\).
Determine the equilibrium constant (\({K_{\text{c}}}\)) assuming all gases are at the same temperature and pressure.
The Contact process involves this homogeneous equilibrium:
\[{\text{2S}}{{\text{O}}_{\text{2}}}{\text{(g)}} + {{\text{O}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2S}}{{\text{O}}_{\text{3}}}{\text{(g)}}\,\,\,\,\,\Delta H = - 198{\text{ kJ}}\]
State the effect of increasing temperature on the value of \({K_{\text{c}}}\) for this reaction.
Outline the economic importance of using a catalyst in the Contact process.
An example of a homogeneous reversible reaction is the reaction between hydrogen and iodine.
\[{{\text{H}}_2}{\text{(g)}} + {{\text{I}}_2}{\text{(g)}} \rightleftharpoons {\text{2HI(g)}}\]
Propene can be hydrogenated in the presence of a nickel catalyst to form propane. Use the data below to answer the questions that follow.

At a temperature just above 700 K it is found that when 1.60 mol of hydrogen and 1.00 mol of iodine are allowed to reach equilibrium in a \({\text{4.00 d}}{{\text{m}}^{\text{3}}}\) flask, the amount of hydrogen iodide formed in the equilibrium mixture is 1.80 mol. Determine the value of the equilibrium constant at this temperature.
Outline why the value for the standard enthalpy change of formation of hydrogen is zero.
Calculate the standard enthalpy change for the hydrogenation of propene.
Calculate the standard entropy change for the hydrogenation of propene.
Determine the value of \(\Delta {G^\Theta }\) for the hydrogenation of propene at 298 K.
At 298 K the hydrogenation of propene is a spontaneous process. Determine the temperature above which propane will spontaneously decompose into propene and hydrogen.
To determine the enthalpy change of combustion of methanol, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{OH}}\), 0.230 g of methanol was combusted in a spirit burner. The heat released increased the temperature of \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of water from 24.5 °C to 45.8 °C.
Methanol can be produced according to the following equation.
\[{\text{CO(g)}} + {\text{2}}{{\text{H}}_2}{\text{(g)}} \to {\text{C}}{{\text{H}}_3}{\text{OH(l)}}\]
The manufacture of gaseous methanol from CO and \({{\text{H}}_{\text{2}}}\) involves an equilibrium reaction.
\({\text{CO(g)}} + {\text{2}}{{\text{H}}_2}{\text{(g)}} \rightleftharpoons {\text{C}}{{\text{H}}_3}{\text{OH(g)}}\) \(\Delta {H^\Theta } < 0\)
Calculate the standard enthalpy change of this reaction, using the values of enthalpy of combustion in Table 12 of the Data Booklet.
Calculate the standard entropy change for this reaction, \(\Delta {S^\Theta }\), using Table 11 of the Data Booklet and given:
\({S^\Theta }{\text{(CO)}} = 198{\text{ J}}\,{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}{\text{ and }}{S^\Theta }{\text{(}}{{\text{H}}_{\text{2}}}{\text{)}} = 131{\text{ J}}\,{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}\).
Calculate, stating units, the standard free energy change for this reaction, \(\Delta {G^\Theta }\), at 298 K.
Predict, with a reason, the effect of an increase in temperature on the spontaneity of this reaction.
1.00 mol of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{OH}}\) is placed in a closed container of volume \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) until equilibrium is reached with CO and \({{\text{H}}_{\text{2}}}\). At equilibrium 0.492 mol of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{OH}}\) are present. Calculate \({K_{\text{c}}}\).
Consider the following equilibrium.
\[\begin{array}{*{20}{l}} {{\text{2S}}{{\text{O}}_2}{\text{(g)}} + {{\text{O}}_2}{\text{(g)}} \rightleftharpoons {\text{2S}}{{\text{O}}_3}{\text{(g)}}}&{\Delta {H^\Theta } = - 198{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}} \end{array}\]
State and explain the effect of increasing the pressure on the yield of sulfur trioxide.
State the effects of a catalyst on the forward and reverse reactions, on the position of equilibrium and on the value of \({K_{\text{c}}}\).
When a mixture of 0.100 mol NO, 0.051 mol \({{\text{H}}_{\text{2}}}\) and 0.100 mol \({{\text{H}}_{\text{2}}}{\text{O}}\) were placed in a \({\text{1.0 d}}{{\text{m}}^{\text{3}}}\) flask at 300 K, the following equilibrium was established.
\(2{\text{NO(g)}} + 2{{\text{H}}_2}{\text{(g)}} \rightleftharpoons {{\text{N}}_2}{\text{(g)}} + 2{{\text{H}}_2}{\text{O(g)}}\)
At equilibrium, the concentration of NO was found to be \({\text{0.062 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Determine the equilibrium constant, \({K_{\text{c}}}\), of the reaction at this temperature.
Outline two differences between an electrolytic cell and a voltaic cell.
Electroplating is an important application of electrolysis. State the composition of the electrodes and the electrolyte used in the silver electroplating process.
Urea, (H2N)2CO, is excreted by mammals and can be used as a fertilizer.
Urea can also be made by the direct combination of ammonia and carbon dioxide gases.
2NH3(g) + CO2(g) \( \rightleftharpoons \) (H2N)2CO(g) + H2O(g) ΔH < 0
Calculate the percentage by mass of nitrogen in urea to two decimal places using section 6 of the data booklet.
Suggest how the percentage of nitrogen affects the cost of transport of fertilizers giving a reason.
The structural formula of urea is shown.
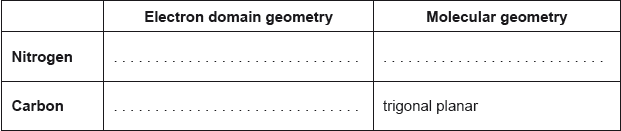
Predict the electron domain and molecular geometries at the nitrogen and carbon atoms, applying the VSEPR theory.
Urea can be made by reacting potassium cyanate, KNCO, with ammonium chloride, NH4Cl.
KNCO(aq) + NH4Cl(aq) → (H2N)2CO(aq) + KCl(aq)
Determine the maximum mass of urea that could be formed from 50.0 cm3 of 0.100 mol dm−3 potassium cyanate solution.
State the equilibrium constant expression, Kc.
Predict, with a reason, the effect on the equilibrium constant, Kc, when the temperature is increased.
Determine an approximate order of magnitude for Kc, using sections 1 and 2 of the data booklet. Assume ΔGΘ for the forward reaction is approximately +50 kJ at 298 K.
Suggest one reason why urea is a solid and ammonia a gas at room temperature.
Sketch two different hydrogen bonding interactions between ammonia and water.
The combustion of urea produces water, carbon dioxide and nitrogen.
Formulate a balanced equation for the reaction.
Calculate the maximum volume of CO2, in cm3, produced at STP by the combustion of 0.600 g of urea, using sections 2 and 6 of the data booklet.
Describe the bond formation when urea acts as a ligand in a transition metal complex ion.
The C–N bonds in urea are shorter than might be expected for a single C–N bond. Suggest, in terms of electrons, how this could occur.
The mass spectrum of urea is shown below.
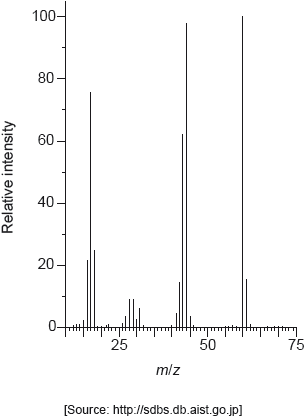
Identify the species responsible for the peaks at m/z = 60 and 44.
The IR spectrum of urea is shown below.
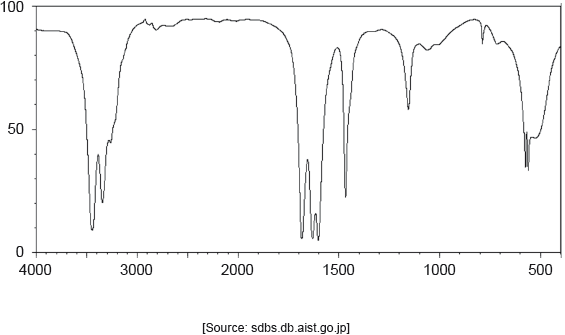
Identify the bonds causing the absorptions at 3450 cm−1 and 1700 cm−1 using section 26 of the data booklet.
Predict the number of signals in the 1H NMR spectrum of urea.
Predict the splitting pattern of the 1H NMR spectrum of urea.
Outline why TMS (tetramethylsilane) may be added to the sample to carry out 1H NMR spectroscopy and why it is particularly suited to this role.
Phosgene, COCl2, is usually produced by the reaction between carbon monoxide and chlorine according to the equation:
(i) Deduce the equilibrium constant expression, Kc, for this reaction.
(ii) At exactly 600°C the value of the equilibrium constant is 0.200. Calculate the standard Gibbs free energy change, , for the reaction, in kJ, using sections 1 and 2 of the data booklet. State your answer to three significant figures.
(iii) The standard enthalpy change of formation of phosgene, \(\Delta H_f^\Theta \), is −220.1kJmol−1. Determine the standard enthalpy change, \(\Delta H_{}^\Theta \), for the forward reaction of the equilibrium, in kJ, using section 12 of the data booklet.
(iv) Calculate the standard entropy change, \(\Delta S_{}^\Theta \), in JK−1, for the forward reaction at 25°C, using your answers to (a) (ii) and (a) (iii). (If you did not obtain an answer to (a) (ii) and/or (a) (iii) use values of +20.0 kJ and −120.0 kJ respectively, although these are not the correct answers.)
One important industrial use of phosgene is the production of polyurethanes. Phosgene is reacted with diamine X, derived from phenylamine.
(i) Classify diamine X as a primary, secondary or tertiary amine.
(ii) Phenylamine, C6H5NH2, is produced by the reduction of nitrobenzene, C6H5NO2. Suggest how this conversion can be carried out.
(iii) Nitrobenzene can be obtained by nitrating benzene using a mixture of concentrated nitric and sulfuric acids. Formulate the equation for the equilibrium established when these two acids are mixed.
(iv) Deduce the mechanism for the nitration of benzene, using curly arrows to indicate the movement of electron pairs.
The other monomer used in the production of polyurethane is compound Z shown below.
(i) State the name, applying IUPAC rules, of compound Z and the class of compounds to which it belongs.
Name:
Class:
(ii) Deduce the number of signals you would expect to find in the 1H NMR spectrum of compound Z, giving your reasons.
The mass spectrum and infrared (IR) spectrum of compound Z are shown below:
Mass spectrum
IR spectrum
(iii) Identify the species causing the large peak at m/z=31 in the mass spectrum.
(iv) Identify the bond that produces the peak labelled Q on the IR spectrum, using section 26 of the data booklet.
Phenylamine can act as a weak base. Calculate the pH of a 0.0100 mol dm−3 solution of phenylamine at 298K using section 21 of the data booklet.