
HL Paper 2
Define the terms acid and base according to the Brønsted-Lowry theory. Distinguish between a weak base and a strong base. State one example of a weak base.
Weak acids in the environment may cause damage. Identify a weak acid in the environment and outline one of its effects.
The graph below indicates the pH change during the titration of \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\) with \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ KOH(aq)}}\). From the graph, identify the volume of KOH(aq) and the pH at the equivalence point.

Explain how the graph could be used to determine the \({\text{p}}{K_{\text{a}}}\) of ethanoic acid and determine the \({\text{p}}{K_{\text{a}}}\) value for these data.
Sketch a graph, similar to the graph on the previous page, to indicate the change in pH during a titration of \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\) with \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) KOH(aq). On your graph, clearly indicate the starting pH value, the equivalence point, the pH at the equivalence point and the final pH reached.
Describe how an indicator works.
Using Table 16 of the Data Booklet, identify the most appropriate indicator for the titration of ethanoic acid with potassium hydroxide. Explain your choice.
Determine the pH of the solution resulting when \({\text{100 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ HCl(aq)}}\) is mixed with \({\text{200 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ NaOH(aq)}}\).
Many reactions are in a state of equilibrium.
The following reaction was allowed to reach equilibrium at 761 K.
H2 (g) + I2 (g) \( \rightleftharpoons \) 2HI (g) ΔHθ < 0
The pH of 0.010 mol dm–3 carbonic acid, H2CO3 (aq), is 4.17 at 25 °C.
H2CO3 (aq) + H2O (l) \( \rightleftharpoons \) HCO3– (aq) + H3O+ (aq).
State the equilibrium constant expression, Kc , for this reaction.
The following equilibrium concentrations in mol dm–3 were obtained at 761 K.
Calculate the value of the equilibrium constant at 761 K.
Determine the value of ΔGθ, in kJ, for the above reaction at 761 K using section 1 of the data booklet.
Calculate [H3O+] in the solution and the dissociation constant, Ka , of the acid at 25 °C.
Calculate Kb for HCO3– acting as a base.
Chloroethene, C2H3Cl, is an important organic compound used to manufacture the polymer poly(chloroethene).
State an equation for the reaction of ethanoic acid with water.
Calculate the pH of \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ethanoic acid \(({\text{p}}{K_{\text{a}}} = 4.76)\).
Determine the pH of a solution formed from adding \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.00 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ethanoic acid, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\), to \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.600 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide, NaOH(aq).
(if acid added) \({\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ - } + {{\text{H}}^ + } \to {\text{C}}{{\text{H}}_3}{\text{COOH}}\);
(if alkali added) \({\text{C}}{{\text{H}}_3}{\text{COOH}} + {\text{O}}{{\text{H}}^ - } \to {\text{C}}{{\text{H}}_3}{\text{CO}}{{\text{O}}^ - } + {{\text{H}}_2}{\text{O}}\);
Explanation marks cannot be awarded without equations.
Graphing is an important tool in the study of rates of chemical reactions.
The graph represents the titration of 25.00 cm3 of 0.100 mol dm−3 aqueous ethanoic acid with 0.100 mol dm−3 aqueous sodium hydroxide.
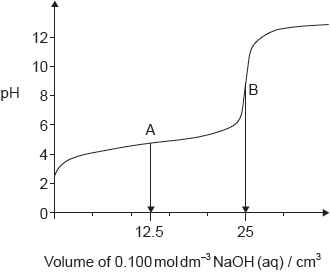
Deduce the major species, other than water and sodium ions, present at points A and B during the titration.
Calculate the pH of 0.100 mol dm−3 aqueous ethanoic acid.
Ka = 1.74 × 10−5
Outline, using an equation, why sodium ethanoate is basic.
Predict whether the pH of an aqueous solution of ammonium chloride will be greater than, equal to or less than 7 at 298 K.
Formulate the equation for the reaction of nitrogen dioxide, NO2, with water to form two acids.
Formulate the equation for the reaction of one of the acids produced in (e)(i) with calcium carbonate.
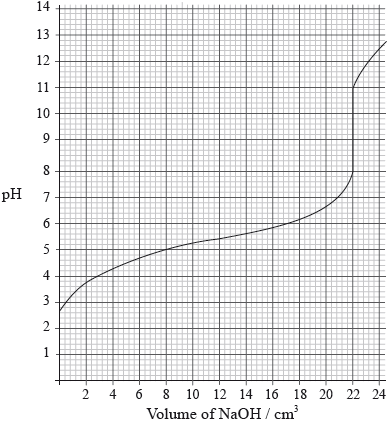
A \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) solution of a weak monoprotic acid, HA(aq), is titrated with \({\text{0.155 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide, NaOH(aq), and the following graph is obtained.
0.100 mol of ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}\), was dissolved in water to make \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) of solution. This solution has a hydroxide ion concentration of \({\text{1.28}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Determine the pH at the equivalence point.
Explain, using an equation, why the equivalence point is not at \({\text{pH}} = 7\).
Calculate the concentration of the weak acid before the addition of any NaOH(aq).
Estimate, using data from the graph, the dissociation constant, \({K_{\text{a}}}\), of the weak acid, HA, showing your working.
Suggest an appropriate indicator for this titration.
Describe qualitatively the action of an acid-base indicator.
Explain what is meant by the term buffer solution.
Calculate the pH of a solution prepared by mixing \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\) and \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of ,\({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ NaOH(aq)}}\) showing your working.
Determine the pH of the solution.
Calculate the base dissociation constant, \({K_{\text{b}}}\), for ammonia.
Limescale, CaCO3(s), can be removed from water kettles by using vinegar, a dilute solution of ethanoic acid, CH3COOH(aq).
Predict, giving a reason, a difference between the reactions of the same concentrations of hydrochloric acid and ethanoic acid with samples of calcium carbonate.
Dissolved carbon dioxide causes unpolluted rain to have a pH of approximately 5, but other dissolved gases can result in a much lower pH. State one environmental effect of acid rain.
Write an equation to show ammonia, NH3, acting as a Brønsted–Lowry base and a different equation to show it acting as a Lewis base.
Determine the pH of 0.010 mol dm−3 2,2-dimethylpropanoic acid solution.
Ka (2,2-dimethylpropanoic acid) = 9.333 × 10−6
Explain, using appropriate equations, how a suitably concentrated solution formed by the partial neutralization of 2,2-dimethylpropanoic acid with sodium hydroxide acts as a buffer solution.
The oxides and chlorides of period 3 elements exhibit periodicity.
Chlorine gas, \({\text{C}}{{\text{l}}_{\text{2}}}{\text{(g)}}\), is bubbled through separate solutions of aqueous bromine, \({\text{B}}{{\text{r}}_{\text{2}}}{\text{(aq)}}\), and potassium bromide, \({\text{KBr(aq)}}\).
The hydrogen halides do not show perfect periodicity. A bar chart of boiling points shows that the boiling point of hydrogen fluoride, HF, is much higher than periodic trends would indicate.

Transition metals form complex ions which are usually coloured.
(i) State the changes in the acid-base nature of the oxides across period 3 (from \({\text{N}}{{\text{a}}_2}{\text{O}}\) to \({\text{C}}{{\text{l}}_{\text{2}}}{{\text{O}}_{\text{7}}}\)), including equations for the reactions of \({\text{N}}{{\text{a}}_2}{\text{O}}\) and \({\text{S}}{{\text{O}}_{\text{3}}}\) with water.
(ii) State whether or not molten aluminium chloride, \({\text{A}}{{\text{l}}_{\text{2}}}{\text{C}}{{\text{l}}_{\text{6}}}\), and molten aluminium oxide, \({\text{A}}{{\text{l}}_{\text{2}}}{{\text{O}}_{\text{3}}}\), conduct electricity. Explain this behaviour in terms of the structure and bonding of the two compounds.
(iii) State the equation for the reaction of \({\text{C}}{{\text{l}}_{\text{2}}}\) with water.
(i) Predict any changes that may be observed in each case.
\({\text{B}}{{\text{r}}_{\text{2}}}{\text{(aq)}}\):
\({\text{KBr(aq)}}\):
(ii) State the half-equations for the reactions that occur.
(i) Explain why the boiling point of HF is much higher than the boiling points of the other hydrogen halides.
(ii) Explain the trend in the boiling points of HCl, HBr and HI.
State the full electron configurations of Cr and \({\text{C}}{{\text{r}}^{3 + }}\).
Cr:
\({\text{C}}{{\text{r}}^{3 + }}\):
\({\text{C}}{{\text{r}}^{3 + }}\) ions and water molecules bond together to form the complex ion \({{\text{[Cr(}}{{\text{H}}_{\text{2}}}{\text{O}}{{\text{)}}_{\text{6}}}{\text{]}}^{3 + }}\).
Describe how the water acts and how it forms the bond, identifying the acid-base character of the reaction.
Explain why the \({{\text{[Cr(}}{{\text{H}}_{\text{2}}}{\text{O}}{{\text{)}}_{\text{6}}}{\text{]}}^{3 + }}\) ion is coloured.
Outline, including a relevant equation, whether the \({{\text{[Cr(}}{{\text{H}}_{\text{2}}}{\text{O}}{{\text{)}}_{\text{6}}}{\text{]}}^{3 + }}\) ion is acidic, basic or neutral.
Explain how the number of electrons in the outer main energy level of phosphorus, P, can be determined using the data of successive ionization energies.
Bleaches in which chlorine is the active ingredient are the most common, although some environmental groups have concerns about their use.
In aqueous chlorine the equilibrium below produces chloric(I) acid (hypochlorous acid), HOCl, the active bleach.
\[{\text{C}}{{\text{l}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HOCl(aq)}} + {{\text{H}}^ + }{\text{(aq)}} + {\text{C}}{{\text{l}}^ - }{\text{(aq)}}\]
Aqueous sodium chlorate(I), NaOCl, the most common active ingredient in chlorine based bleaches, oxidizes coloured materials to colourless products while being reduced to the chloride ion. It will also oxidize sulfur dioxide to the sulfate ion.
The standard electrode potential for the reduction of the chlorate(V) ion to the chloride ion is \( + 1.49{\text{ V}}\).
(i) Describe the colour change that occurs when aqueous chlorine is added to aqueous sodium bromide.
(ii) Outline, with the help of a chemical equation, why this reaction occurs.
Chloric(I) acid is a weak acid, but hydrochloric acid is a strong acid. Outline how this is indicated in the equation above.
State a balanced equation for the reaction of chloric(I) acid with water.
Outline, in terms of the equilibrium in aqueous chlorine, why it is dangerous to use an acidic toilet cleaner in combination with this kind of bleach.
Suggest why a covalent molecule, such as chloric(I) acid, is readily soluble in water.
Partial neutralization of chloric(I) acid creates a buffer solution. Given that the \({\text{p}}{K_{\text{a}}}\) of chloric(I) acid is 7.53, determine the pH of a solution that has \({\text{[HOCl]}} = 0.100{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) and \({\text{[Cl}}{{\text{O}}^ - }{\text{]}} = 0.0500{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Describe, using HIn to represent the indicator in its acid form, why an indicator changes colour when excess alkali is added.
(i) Deduce a balanced equation for the reaction between the chlorate(I) ion and sulfur dioxide from the appropriate half-equations.
(ii) State the initial and final oxidation numbers of both chlorine and sulfur in the final equation.

(i) Define the term standard electrode potential.
(ii) Referring to Table 14 of the Data Booklet, deduce, giving a reason, whether the oxidation of the chromium(III) ion to the dichromate(VI) ion by the chlorate(V) ion is energetically feasible.
The Haber process enables the large-scale production of ammonia needed to make fertilizers.
The equation for the Haber process is given below.
\[{{\text{N}}_2}({\text{g)}} + 3{{\text{H}}_2}({\text{g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_3}({\text{g)}}\]
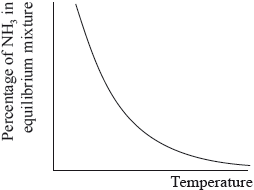
The percentage of ammonia in the equilibrium mixture varies with temperature.
Ammonia can be converted into nitric acid, \({\text{HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\), and hydrocyanic acid, HCN(aq). The \({\text{p}}{K_{\text{a}}}\) of hydrocyanic acid is 9.21.
A student decided to investigate the reactions of the two acids with separate samples of \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.
(i) Use the graph to deduce whether the forward reaction is exothermic or endothermic and explain your choice.
(ii) State and explain the effect of increasing the pressure on the yield of ammonia.
(iii) Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction.
(iv) A mixture of 1.00 mol \({{\text{N}}_{\text{2}}}\) and 3.00 mol \({{\text{H}}_{\text{2}}}\) was placed in a \({\text{1.0 d}}{{\text{m}}^{\text{3}}}\) flask at 400 °C. When the system was allowed to reach equilibrium, the concentration of was found to be \({\text{0.062 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Determine the equilibrium constant, \({K_{\text{c}}}\), of the reaction at this temperature.
(v) Iron is used as a catalyst in the Haber process. State the effect of a catalyst on the value of \({K_{\text{c}}}\).
(i) Distinguish between the terms strong and weak acid and state the equations used to show the dissociation of each acid in aqueous solution.
(ii) Deduce the expression for the ionization constant, \({K_{\text{a}}}\), of hydrocyanic acid and calculate its value from the \({\text{p}}{K_{\text{a}}}\) value given.
(iii) Use your answer from part (b) (ii) to calculate the \({\text{[}}{{\text{H}}^ + }{\text{]}}\) and the pH of an aqueous solution of hydrocyanic acid of concentration \({\text{0.108 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). State one assumption made in arriving at your answer.
A small piece of magnesium ribbon is added to solutions of nitric and hydrocyanic acid of the same concentration at the same temperature. Describe two observations that would allow you to distinguish between the two acids.
(i) Calculate the volume of the sodium hydroxide solution required to react exactly with a \({\text{15.0 c}}{{\text{m}}^{\text{3}}}\) solution of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) nitric acid.
(ii) The following hypothesis was suggested by the student: “Since hydrocyanic acid is a weak acid it will react with a smaller volume of the \({\text{0.20 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution.” Comment on whether or not this is a valid hypothesis.
(iii) Use Table 16 of the Data Booklet to identify a suitable indicator for the titration of sodium hydroxide and hydrocyanic acid.
The \({\text{p}}{K_{\text{a}}}\) value for propanoic acid is given in Table 15 of the Data Booklet.
State the equation for the reaction of propanoic acid with water.
Calculate the hydrogen ion concentration (in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\)) of an aqueous solution of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) propanoic acid.
The graph below shows a computer simulation of a titration of \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid with \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide and the pH range of phenol red indicator.
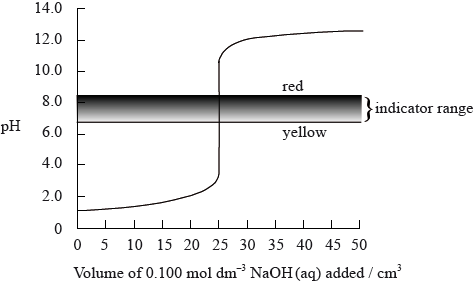
Sketch the graph that would be obtained for the titration of \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) propanoic acid with \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) potassium hydroxide using bromophenol blue as an indicator. (The pH range of bromophenol blue can be found in Table 16 of the Data Booklet).
Acid–base chemistry can play a major role in chemical and biological processes.
White vinegar, which contains ethanoic acid, CH3COOH, can be used as a cleaning agent to dissolve mineral deposits from coffee machines.
Buffer solutions play a pivotal role in solution chemistry.
Acid–base indicators are often organic dyes.
Ammonia, NH3, can be used to clean ovens. The concentration of hydroxide ions, OH–(aq), in a solution of ammonia is \({\text{3.98}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). Calculate its pH, correct to one decimal place, at 298 K.
Define an acid according to the Brønsted–Lowry theory and the Lewis theory.
Brønsted–Lowry theory:
Lewis theory:
Ethanoic acid is an example of a weak acid. Distinguish between a strong acid and a weak acid in terms of the extent of dissociation.
State whether the following mixtures, in the appropriate molar ratios, can be classified as buffer solutions. Show your answer by stating yes or no in the table below.

Describe qualitatively the action of an acid–base indicator.
Using Table 16 of the Data Booklet, identify the most appropriate indicator for the titration of ethanoic acid with sodium hydroxide. Explain your choice.
\({\text{150 c}}{{\text{m}}^{\text{3}}}\) of \({\text{5.00}} \times {\text{1}}{{\text{0}}^{ - 1}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) HCl (aq) is mixed with \({\text{300 c}}{{\text{m}}^{\text{3}}}\) of \({\text{2.03}} \times {\text{1}}{{\text{0}}^{ - 1}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) NaOH(aq). Determine the pH of the solution, correct to two decimal places.
An equilibrium exists between nitrosyl chloride, NOCl, nitrogen oxide, NO, and chlorine, \({\text{C}}{{\text{l}}_{\text{2}}}\).
\[{\text{2NOCl(g)}} \rightleftharpoons {\text{2NO(g)}} + {\text{C}}{{\text{l}}_2}{\text{(g)}}\]
\({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of hexane, \({{\text{C}}_{\text{6}}}{{\text{H}}_{{\text{14}}}}\), and \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of pentan-1-ol, \({{\text{C}}_{\text{5}}}{{\text{H}}_{{\text{11}}}}{\text{OH}}\), were placed separately into two closed containers at 298 K and allowed to reach equilibrium.
Ammonia is a weak base.
(i) Deduce the equilibrium constant expression for this reaction.
(ii) Explain the effect on the position of equilibrium and the value of \({K_{\text{c}}}\) when pressure is decreased and temperature is kept constant.
(iii) 2.00 mol of NOCl was placed in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container and allowed to reach equilibrium at 298 K. At equilibrium, 0.200 mol of NO was present. Determine the equilibrium concentrations of NOCl and \({\text{C}}{{\text{l}}_{\text{2}}}\), and hence calculate the value of \({K_{\text{c}}}\) at this temperature.
(iv) The value of \({K_{\text{c}}}\) is \(1.60 \times {10^{ - 5}}\) at 318 K. State and explain whether the forward reaction is exothermic or endothermic.
(i) Compare the two liquids in terms of their boiling points, enthalpies of vaporization and vapour pressures.
(ii) Explain your answer given for part (b)(i).
Calculate the pH of a \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia at 298 K to two decimal places, using Table 15 of the Data Booklet.
A buffer solution is made using \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid, HCl (aq), and \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\).
Describe the meaning of the term buffer solution.
Determine the pH of the buffer solution at 298 K.
A \({\text{1.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia is added to \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of a \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid solution in a titration experiment.
Calculate the total volume of the solution at the equivalence point.
Calculate the pH of the solution at the equivalence point, using Table 15 of the Data Booklet.
Identify a suitable indicator for this titration, using Table 16 of the Data Booklet.
A group of students investigated the rate of the reaction between aqueous sodium thiosulfate and hydrochloric acid according to the equation below.
\[{\text{N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3}{\text{(aq)}} + {\text{2HCl(aq)}} \to {\text{2NaCl(aq)}} + {\text{S}}{{\text{O}}_2}{\text{(g)}} + {\text{S(s)}} + {{\text{H}}_2}{\text{O(l )}}\]
The two reagents were rapidly mixed together in a beaker and placed over a mark on a piece of paper. The time taken for the precipitate of sulfur to obscure the mark when viewed through the reaction mixture was recorded.
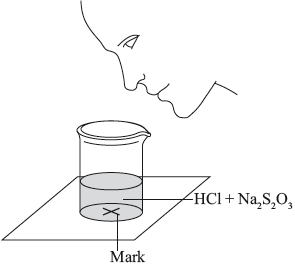
Initially they measured out \({\text{10.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid and then added \({\text{40.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.0200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous sodium thiosulfate. The mark on the paper was obscured 47 seconds after the solutions were mixed.
One proposed mechanism for this reaction is:
\({{\text{S}}_2}{\text{O}}_3^{2 - }{\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}} \rightleftharpoons {\text{H}}{{\text{S}}_2}{\text{O}}_3^ - {\text{(aq)}}\) Fast
\({\text{H}}{{\text{S}}_2}{\text{O}}_3^ - {\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}} \to {\text{S}}{{\text{O}}_2}{\text{(g)}} + {\text{S(s)}} + {{\text{H}}_2}{\text{O(l)}}\) Slow
The teacher asked the students to devise another technique to measure the rate of this reaction.
Another group suggested collecting the sulfur dioxide and drawing a graph of the volume of gas against time.
(i) State the volumes of the liquids that should be mixed.

(ii) State why it is important that the students use a similar beaker for both reactions.
(iii) If the reaction were first order with respect to the thiosulfate ion, predict the time it would take for the mark on the paper to be obscured when the concentration of sodium thiosulfate solution is halved.
(i) Deduce the rate expression of this mechanism.
(ii) The results of an experiment investigating the effect of the concentration of hydrochloric acid on the rate, while keeping the concentration of thiosulfate at the original value, are given in the table below.

On the axes provided, draw an appropriate graph to investigate the order of the reaction with respect to hydrochloric acid.
(iii) Identify two ways in which these data do not support the rate expression deduced in part (i).
(i) Sketch and label, indicating an approximate activation energy, the Maxwell–Boltzmann energy distribution curves for two temperatures, \({T_1}\) and \(T2{\text{ }}({T_2} > {T_1})\), at which the rate of reaction would be significantly different.

(ii) Explain why increasing the temperature of the reaction mixture would significantly increase the rate of the reaction.
(i) One group suggested recording how long it takes for the pH of the solution to change by one unit. Calculate the initial pH of the original reaction mixture.
(ii) Deduce the percentage of hydrochloric acid that would have to be used up for the pH to change by one unit.
Calculate the volume of sulfur dioxide, in \({\text{c}}{{\text{m}}^{\text{3}}}\), that the original reaction mixture would produce if it were collected at \(1.00 \times {10^5}{\text{ Pa}}\) and 300 K.
Sulfur dioxide, a major cause of acid rain, is quite soluble in water and the equilibrium shown below is established.
\({\text{S}}{{\text{O}}_2}{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HSO}}_3^ - {\text{(aq)}} + {{\text{H}}^ + }{\text{(aq)}}\)
Given that the \({K_{\text{a}}}\) for this equilibrium is \(1.25 \times {10^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\), determine the pH of a \(2.00{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of sulfur dioxide.
Using Table 15 of the Data Booklet, identify an organic acid that is a stronger acid than sulfur dioxide.
Antimony, Sb, forms a fluoride, \({\text{Sb}}{{\text{F}}_{\text{5}}}\).
The equilibrium that occurs when antimony(V) fluoride is dissolved in liquid hydrogen fluoride can be represented by the equation below.
\[{\text{Sb}}{{\text{F}}_5}{\text{(s)}} + {\text{2HF(l)}} \rightleftharpoons {\text{SbF}}_6^ - {\text{(sol)}} + {{\text{H}}_2}{{\text{F}}^ + }{\text{(sol)}}\]
Outline how the following factors account for the fact that HCl is a strong acid and HF is a weak acid.
Some students were provided with a \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of a monobasic acid, HQ, and given the problem of determining whether HQ was a weak acid or a strong acid.
The second problem set for the students was to determine the acid dissociation constant, \({K_{\text{a}}}\), of the acid HQ and its \({\text{p}}{K_{\text{a}}}\).
State the element that you would expect to have chemical properties most similar to those of antimony.
Describe the relationship between \({\text{Sb}}{{\text{F}}_{\text{5}}}\) and \({\text{SbF}}_6^ - \) in terms of the Lewis theory of acids.
Explain the behaviour of HF in terms of the Brønsted–Lowry theory of acids.
The strength of the hydrogen–halogen bond.
The interaction between an undissociated hydrogen halide molecule and a water molecule.
Neelu and Charles decided to solve the problem by determining the volume of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide solution needed to neutralize \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of the acid. Outline whether this was a good choice.
Identify one indicator that could be used when titrating aqueous sodium hydroxide with both a strong acid and a weak acid, and outline the reason for your choice.
Indicator:
Reason:
Neelu and Charles decided to compare the volume of sodium hydroxide solution needed with those required by known \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) strong and weak acids. Unfortunately they chose sulfuric acid as the strong acid. Outline why this was an unsuitable choice.
Francisco and Shamiso decided to measure the pH of the initial solution, HQ, and they found that its pH was 3.7. Deduce, giving a reason, the strength (weak or strong) of the acid HQ.
Explain how the \({\text{p}}{K_{\text{a}}}\) could be determined from a graph of pH against the volume of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium hydroxide added.
Francisco and Shamiso found that the pH of the initial \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution was 3.7. However, this reading was inaccurate because they forgot to wash the pH probe. Calculate the \({\text{p}}{K_{\text{a}}}\) of HQ using the reading they obtained.
Ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}\), is a weak base. It has a \({\text{p}}{K_{\text{b}}}\) value of 4.75.
Salts may form neutral, acidic or alkaline solutions when dissolved in water.
Another weak base is nitrogen trifluoride, \({\text{N}}{{\text{F}}_{\text{3}}}\). Explain how \({\text{N}}{{\text{F}}_{\text{3}}}\) is able to function as a Lewis base.
Calculate the pH of a \({\text{1.00}} \times {\text{1}}{{\text{0}}^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous solution of ammonia at 298 K.
\({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \(1.00 \times {10^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid solution is added to \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.00}} \times {\text{1}}{{\text{0}}^{ - 2}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous ammonia solution. Calculate the concentrations of both ammonia and ammonium ions in the resulting solution and hence determine the pH of the solution.
State what is meant by a buffer solution and explain how the solution in (v), which contains ammonium chloride dissolved in aqueous ammonia, can function as a buffer solution.
State the equations for the reactions of sodium oxide, \({\text{N}}{{\text{a}}_{\text{2}}}{\text{O}}\), and phosphorus(V)oxide, \({{\text{P}}_{\text{4}}}{{\text{O}}_{{\text{10}}}}\), with water.
Some of the most important processes in chemistry involve acid-base reactions.
Calculate the \({K_{\text{a}}}\) value of benzoic acid, \({{\text{C}}_{\text{6}}}{{\text{H}}_{\text{5}}}{\text{COOH}}\), using Table 15 in the Data Booklet.
Based on its \({K_{\text{a}}}\) value, state and explain whether benzoic acid is a strong or weak acid.
Determine the hydrogen ion concentration and the pH of a \({\text{0.010 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) benzoic acid solution. State one assumption made in your calculation.
Hypochlorous acid, HOCl(aq), is an example of a weak acid.
A household bleach contains sodium hypochlorite, NaOCl(aq), at a concentration of \({\text{0.705 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\). The hypochlorite ion, \({\text{OC}}{{\text{l}}^ - }{\text{(aq)}}\) is a weak base.
\[{\text{OC}}{{\text{l}}^ - }{\text{(aq)}} + {{\text{H}}_2}{\text{O(l)}} \rightleftharpoons {\text{HOCl(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]
State the expression for the ionic product constant of water, \({K_{\text{w}}}\).
The \({\text{p}}{K_{\text{a}}}\) value of HOCl(aq) is 7.52. Determine the \({K_{\text{b}}}\) value of \({\text{OC}}{{\text{l}}^ - }{\text{(aq)}}\) assuming a temperature of 298 K.
Determine the concentration of \({\text{O}}{{\text{H}}^ - }{\text{(aq)}}\), in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\), at equilibrium and state one assumption made in arriving at your answer other than a temperature of 298 K.
Calculate the pH of the bleach.
The element boron has two naturally occurring isotopes, \(^{{\text{10}}}{\text{B}}\) and \(^{{\text{11}}}{\text{B}}\).
Phosphorus forms two chlorides, \({\text{PC}}{{\text{l}}_{\text{3}}}\) and \({\text{PC}}{{\text{l}}_{\text{5}}}\).
Apply the Aufbau principle to state the full electron configuration for an atom of phosphorus.
Deduce the Lewis structures for \({\text{PC}}{{\text{l}}_{\text{3}}}\) and \({\text{PC}}{{\text{l}}_{\text{5}}}\).
\({\text{PC}}{{\text{l}}_{\text{3}}}\)\(\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \)\({\text{PC}}{{\text{l}}_{\text{5}}}\)
Predict the shapes and the bond angles in the two molecules.

Identify the type of hybridization present in \({\text{PC}}{{\text{l}}_{\text{3}}}\).
Compare the melting points of \({\text{PC}}{{\text{l}}_{\text{3}}}\) and \({\text{PC}}{{\text{l}}_{\text{5}}}\) and explain the difference.
Define an acid according to the Lewis theory.
State and explain the acid–base character of \({\text{PC}}{{\text{l}}_{\text{3}}}\) according to the Lewis theory.
Explain the delocalization of \(\pi \) electrons using the \({{\text{O}}_{\text{3}}}\) molecule as an example, including two facts that support the delocalization.
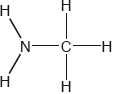
Two hydrides of nitrogen are ammonia and hydrazine, \({{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}\). One derivative of ammonia is methanamine whose molecular structure is shown below.
Hydrazine is used to remove oxygen from water used to generate steam or hot water.
\[{{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(aq)}} + {{\text{O}}_{\text{2}}}{\text{(aq)}} \to {{\text{N}}_{\text{2}}}{\text{(g)}} + {\text{2}}{{\text{H}}_{\text{2}}}{\text{O(l)}}\]
The concentration of dissolved oxygen in a sample of water is \(8.0 \times {10^{ - 3}}{\text{ g}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Estimate the H−N−H bond angle in methanamine using VSEPR theory.
State the electron domain geometry around the nitrogen atom and its hybridization in methanamine.
Ammonia reacts reversibly with water.
\[{\text{N}}{{\text{H}}_{\text{3}}}{\text{(g)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}} \rightleftharpoons {\text{NH}}_{\text{4}}^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]
Explain the effect of adding \({{\text{H}}^ + }{\text{(aq)}}\) ions on the position of the equilibrium.
Hydrazine reacts with water in a similar way to ammonia. (The association of a molecule of hydrazine with a second H+ is so small it can be neglected.)
\[{{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(aq)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}} \rightleftharpoons {{\text{N}}_{\text{2}}}{\text{H}}_{\text{5}}^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]
\[{\text{p}}{K_{\text{b}}}{\text{ (hydrazine)}} = 5.77\]
Calculate the pH of a \(0.0100{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of hydrazine.
Suggest a suitable indicator for the titration of hydrazine solution with dilute sulfuric acid using section 22 of the data booklet.
Outline, using an ionic equation, what is observed when magnesium powder is added to a solution of ammonium chloride.
Determine the enthalpy change of reaction, \(\Delta H\), in kJ, when 1.00 mol of gaseous hydrazine decomposes to its elements. Use bond enthalpy values in section 11 of the data booklet.
\[{{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(g)}} \to {{\text{N}}_{\text{2}}}{\text{(g)}} + {\text{2}}{{\text{H}}_{\text{2}}}{\text{(g)}}\]
The standard enthalpy of formation of \({{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(l)}}\) is \( + 50.6{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). Calculate the enthalpy of vaporization, \(\Delta {H_{{\text{vap}}}}\), of hydrazine in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). \[{{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(l)}} \to {{\text{N}}_{\text{2}}}{{\text{H}}_{\text{4}}}{\text{(g)}}\] (If you did not get an answer to (f), use \( - 85{\text{ kJ}}\) but this is not the correct answer.)
Calculate, showing your working, the mass of hydrazine needed to remove all the dissolved oxygen from \({\text{1000 d}}{{\text{m}}^{\text{3}}}\) of the sample.
Calculate the volume, in \({\text{d}}{{\text{m}}^{\text{3}}}\), of nitrogen formed under SATP conditions. (The volume of 1 mol of gas = \({\text{24.8 d}}{{\text{m}}^{\text{3}}}\) at SATP.)
A buffer solution is made using \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) nitric acid, \({\text{HN}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\), and \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{1.00 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\).
Bromocresol green is an acid–base indicator. Information about bromocresol green is given in Table 16 of the Data Booklet.
A solution of ammonia has a concentration of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\).
Calculate the pH of the ammonia solution using information from Table 15 of the Data Booklet. State one assumption made.
(i) State the meaning of the term buffer solution.
(ii) Calculate the concentrations of ammonia and ammonium ion in the buffer solution.
(iii) Determine the pH of the buffer solution at 25 °C.
(iv) Explain why the pH of the buffer solution is different from the pH of the ammonia solution calculated in (d).
(v) Explain the action of the buffer solution when a few drops of nitric acid solution are added to it.
(i) Identify the property of bromocresol green that makes it suitable to use as an acid–base indicator.
(ii) State and explain the relationship between the pH range of bromocresol green and its \({\text{p}}{K_{\text{a}}}\) value.
Iron has three main naturally occurring isotopes which can be investigated using a mass spectrometer.
State the full electronic configurations of a Cu atom and a \({\text{C}}{{\text{u}}^ + }\) ion.
Cu:
\({\text{C}}{{\text{u}}^ + }\):
Explain the origin of colour in transition metal complexes and use your explanation to suggest why copper(II) sulfate, CuSO4(aq), is blue, but zinc sulfate, ZnSO4(aq), is colourless.
\({\text{C}}{{\text{u}}^{2 + }}{\text{(aq)}}\) reacts with ammonia to form the complex ion \({{\text{[Cu(N}}{{\text{H}}_{\text{3}}}{{\text{)}}_{\text{4}}}{\text{]}}^{2 + }}\). Explain this reaction in terms of an acid-base theory, and outline how the bond is formed between \({\text{C}}{{\text{u}}^{2 + }}\) and \({\text{N}}{{\text{H}}_{\text{3}}}\).
When nitrogen gas and hydrogen gas are allowed to react in a closed container the following equilibrium is established.
\[{{\text{N}}_{\text{2}}}{\text{(g)}} + {\text{3}}{{\text{H}}_{\text{2}}}{\text{(g)}} \rightleftharpoons {\text{2N}}{{\text{H}}_{\text{3}}}{\text{(g) }}\Delta H = -92.6{\text{ kJ}}\]
Outline two characteristics of a reversible reaction in a state of dynamic equilibrium.
Predict, with a reason, how each of the following changes affects the position of equilibrium.
The volume of the container is increased.
Ammonia is removed from the equilibrium mixture.
Define the term activation energy, \({E_{\text{a}}}\).
Ammonia is manufactured by the Haber process in which iron is used as a catalyst.
Explain the effect of a catalyst on the rate of reaction.
Typical conditions used in the Haber process are 500 °C and 200 atm, resulting in approximately 15% yield of ammonia.
(i) Explain why a temperature lower than 500 °C is not used.
(ii) Outline why a pressure higher than 200 atm is not often used.
Deduce the equilibrium constant expression, \({K_{\text{c}}}\), for the reaction on page 10.
When 1.00 mol of nitrogen and 3.00 mol of hydrogen were allowed to reach equilibrium in a \({\text{1.00 d}}{{\text{m}}^{\text{3}}}\) container at a temperature of 500 °C and a pressure of 1000 atm, the equilibrium mixture contained 1.46 mol of ammonia.
Calculate the value of \({K_{\text{c}}}\) at 500 °C.
Define the term base according to the Lewis theory.
Define the term weak base according to the Brønsted–Lowry theory.
Deduce the formulas of conjugate acid-base pairs in the reaction below.
\[{\text{C}}{{\text{H}}_{\text{3}}}{\text{N}}{{\text{H}}_{\text{2}}}{\text{(aq)}} + {{\text{H}}_{\text{2}}}{\text{O(l)}} \rightleftharpoons {\text{C}}{{\text{H}}_{\text{3}}}{\text{NH}}_{\text{3}}^ + {\text{(aq)}} + {\text{O}}{{\text{H}}^ - }{\text{(aq)}}\]

Determine the pH of a \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) solution of ammonia, \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\), using tables 2 and 15 of the data booklet.
(i) Sketch the pH titration curve obtained when \({\text{50.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\) is added to \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.100 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{HCl (aq)}}\).
(ii) Identify an indicator from table 16 of the data booklet that could be used for this titration.
A student used a pH meter to measure the pH of different samples of water at 298 K.
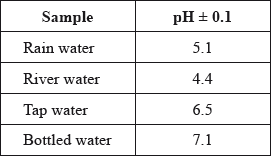
Use the data in the table to identify the most acidic water sample.
Calculate the percentage uncertainty in the measured pH of the rain water sample.
Determine the ratio of \({\text{[}}{{\text{H}}^ + }{\text{]}}\) in bottled water to that in rain water.
\[\frac{{[{H^ + }]{\text{ }}in{\text{ }}bottled{\text{ }}water}}{{[{H^ + }]{\text{ }}in{\text{ }}rain{\text{ }}water}}\]
Determine the concentration of hydroxide ions in the sample of river water.
The acidity of non-polluted rain water is caused by dissolved carbon dioxide. State an equation for the reaction of carbon dioxide with water.
A buffer solution with a pH of 3.87 contains \({\text{7.41 g}}\,{\text{d}}{{\text{m}}^{ - 3}}\) of propanoic acid, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{COOH}}\), together with an unknown quantity of sodium propanoate, \({\text{C}}{{\text{H}}_{\text{3}}}{\text{C}}{{\text{H}}_{\text{2}}}{\text{COONa}}\).
Define the term buffer solution.
Explain, using appropriate equations, how this solution acts as a buffer solution.
Calculate the concentration, in \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\), of sodium propanoate in this buffer solution.
The \({\text{p}}{K_{\text{a}}}\) of propanoic acid is 4.87 at 298 K.
Acids can be described as strong or weak.
(i) Outline the difference in dissociation between strong and weak acids of the same concentration.
(ii) Describe three tests that can be carried out in the laboratory, and the expected results, to distinguish between \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ HCl(aq)}}\) and \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ C}}{{\text{H}}_{\text{3}}}{\text{COOH(aq)}}\).
Calculate the pH, using table 15 of the data booklet, of a solution of ethanoic acid made by dissolving 1.40 g of the acid in distilled water to make a \({\text{500 c}}{{\text{m}}^{\text{3}}}\) solution.
Determine the pH at the equivalence point of the titration and the \({\text{p}}{K_{\text{a}}}\) of an unknown acid using the acid-base titration curve below.
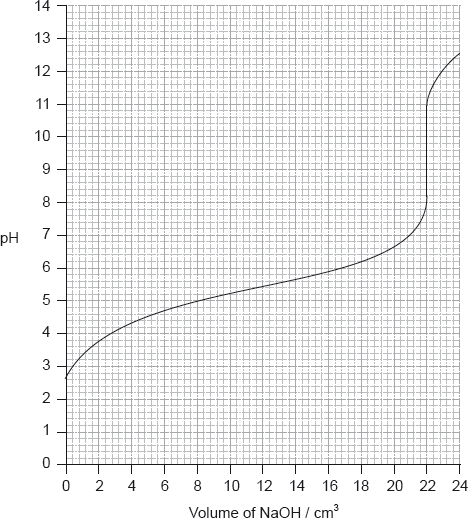
Identify, using table 16 of the data booklet, a suitable indicator to show the end-point of this titration.
Describe how an indicator, that is a weak acid, works. Use Le Chatelier’s principle in your answer.
State the formula of the conjugate base of chloroethanoic acid, \({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCOOH}}\).
Identify, with a reason, whether chloroethanoic acid is weaker or stronger than ethanoic acid using table 15 of the data booklet.
Determine the pH of the solution resulting when \({\text{100 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.50 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) \({\text{C}}{{\text{H}}_{\text{2}}}{\text{ClCOOH}}\) is mixed with \({\text{200 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) NaOH.
Describe how chlorine’s position in the periodic table is related to its electron arrangement.
\({\text{SC}}{{\text{l}}_{\text{2}}}\) and \({\text{SCl}}{{\text{F}}_{\text{5}}}\) are two sulfur chloride type compounds with sulfur having different oxidation states. Predict the name of the shape, the bond angle and polarity of these molecules.
Iron rusts in the presence of oxygen and water. Rusting is a redox process involving several steps that produces hydrated iron(III) oxide, \({\text{F}}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}} \bullet {\text{n}}{{\text{H}}_{\text{2}}}{\text{O}}\), as the final product.
The half-equations involved for the first step of rusting are given below.
Half-equation 1: \({\text{Fe(s)}} \to {\text{F}}{{\text{e}}^{2 + }}{\text{(aq)}} + {\text{2}}{{\text{e}}^ - }\)
Half-equation 2: \({{\text{O}}_{\text{2}}}{\text{(aq)}} + {\text{4}}{{\text{e}}^ - } + {\text{2}}{{\text{H}}_{\text{2}}}{\text{O(l)}} \to {\text{4O}}{{\text{H}}^ - }{\text{(aq)}}\)
(i) Identify whether half-equation 1 represents oxidation or reduction, giving a reason for your answer.
(ii) Identify the oxidation number of each atom in the three species in half-equation 2.
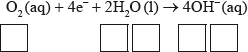
(iii) Deduce the overall redox equation for the first step of rusting by combining half-equations 1 and 2.
(iv) Identify the reducing agent in the redox equation in part (iii).
The oxygen in half-equation 2 is atmospheric oxygen that is found dissolved in water in very small concentrations. Explain, in terms of intermolecular forces, why oxygen is not very soluble in water.
State the relationship between the electron arrangement of an element and its group and period in the periodic table.
Transition metals and their compounds often catalyse reactions. The catalyzed decomposition of hydrogen peroxide by CuO is an example. State two other examples of catalyzed reactions giving the transition metal or its compound acting as catalyst.
(i) State a chemical equation for the partial dissociation of water into ions, including state symbols.
(ii) The dissociation of water into ions is reversible. State the expression for the ionic product constant of water.
(iii) The ionic product constant of water was measured at three different temperatures.
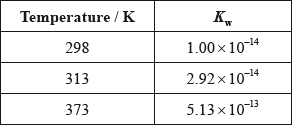
Deduce whether the ionization of water is exothermic or endothermic, giving your reason.
(iv) Use the data in part (iii) to determine the pH of water at 373 K, correct to two decimal places.
(i) An aqueous solution of sodium chloride is electrolysed using inert electrodes. Explain which product is obtained at the positive electrode (anode) if the concentration of sodium chloride is high.
(ii) State the half-equations occurring at the electrodes during the electrolysis of the concentrated aqueous solution of sodium chloride.
Negative electrode (cathode):
Positive electrode (anode):
Describe how electrolysis can be used to electroplate a bracelet with a layer of silver metal. Include the choice of electrodes and electrolyte needed in your description.
A sample of magnesium contains three isotopes: magnesium-24, magnesium-25 and magnesium-26, with abundances of 77.44%, 10.00% and 12.56% respectively.
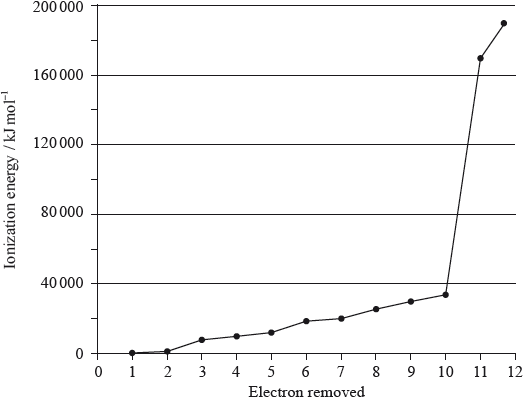
A graph of the successive ionization energies of magnesium is shown below.
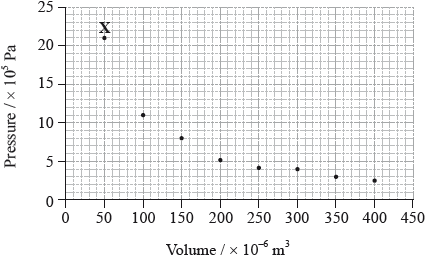
The graph below shows pressure and volume data collected for a sample of carbon dioxide gas at 330 K.
(i) Calculate the relative atomic mass of this sample of magnesium correct to two decimal places.
(ii) Predict the relative atomic radii of the three magnesium isotopes, giving your reasons.
(i) Explain the increase in ionization energy values from the 3rd to the 8th electrons.
(ii) Explain the sharp increase in ionization energy values between the 10th and 11th electrons.
(i) Magnesium reacts with oxygen to form an ionic compound, magnesium oxide. Describe how the ions are formed, and the structure and bonding in magnesium oxide.
(ii) Carbon reacts with oxygen to form a covalent compound, carbon dioxide. Describe what is meant by a covalent bond.
(iii) State why magnesium and oxygen form an ionic compound while carbon and oxygen form a covalent compound.
(i) Predict the type of hybridization of the carbon and oxygen atoms in \({\text{C}}{{\text{O}}_{\text{2}}}\).
(ii) Sketch the orbitals of an oxygen atom in \({\text{C}}{{\text{O}}_{\text{2}}}\) on the energy level diagram provided, including the electrons that occupy each orbital.

(iii) Define the term electronegativity.
(iv) Explain why oxygen has a larger electronegativity than carbon.
(i) Draw a best-fit curve for the data on the graph.
(ii) Use the data point labelled X to determine the amount, in mol, of carbon dioxide gas in the sample.
(i) Most indicators are weak acids. Describe qualitatively how indicators work.
(ii) Identify a suitable indicator for a titration between a weak acid and a strong base, using Table 16 of the Data Booklet.
A student decided to determine the molecular mass of a solid monoprotic acid, HA, by titrating a solution of a known mass of the acid.
The following recordings were made.

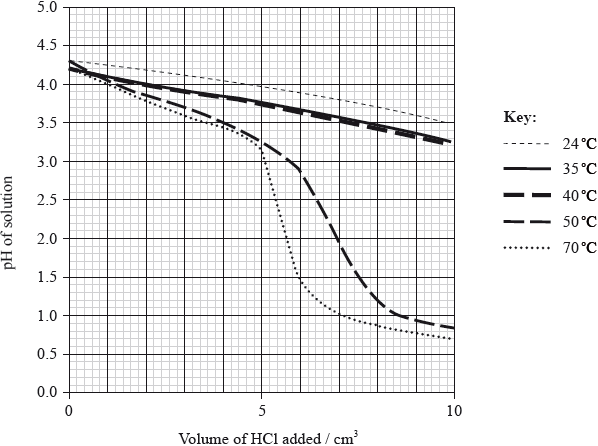
To investigate the effect of temperature on the effectiveness of a buffer solution, the student placed \({\text{20.0 c}}{{\text{m}}^{\text{3}}}\) of the buffer solution in a water bath at 24 °C. He added small portions of hydrochloric acid, stirring after each addition, until a total of \({\text{10 c}}{{\text{m}}^{\text{3}}}\) was added, and measured the pH continuously during the addition. The procedure was repeated at different temperatures and the results are shown in the following graph.
Determine the molecular formula of HA.
State what is meant by a buffer solution.
With reference to the graph on page 4, describe the effect of increasing temperature on the effectiveness of the buffer solution.
Trends in physical and chemical properties are useful to chemists.
Cobalt forms the transition metal complex [Co(NH3)4 (H2O)Cl]Br.
Explain why the melting points of the group 1 metals (Li → Cs) decrease down the group whereas the melting points of the group 17 elements (F → I) increase down the group.
State the shape of the complex ion.
Deduce the charge on the complex ion and the oxidation state of cobalt.
Describe, in terms of acid-base theories, the type of reaction that takes place between the cobalt ion and water to form the complex ion.
Phosphorus(V) oxide, \({{\text{P}}_{\text{4}}}{{\text{O}}_{{\text{10}}}}{\text{ }}({M_{\text{r}}} = 283.88)\), reacts vigorously with water \(({M_{\text{r}}} = 18.02)\), according to the equation below.
\[{{\text{P}}_{\text{4}}}{{\text{O}}_{{\text{10}}}}{\text{(s)}} + {\text{6}}{{\text{H}}_{\text{2}}}{\text{O(l)}} \to {\text{4}}{{\text{H}}_{\text{3}}}{\text{P}}{{\text{O}}_{\text{4}}}{\text{(aq)}}\]
A student added 5.00 g of \({{\text{P}}_{\text{4}}}{{\text{O}}_{{\text{10}}}}\) to 1.50 g of water. Determine the limiting reactant, showing your working.
Calculate the mass of phosphoric(V) acid, \({{\text{H}}_{\text{3}}}{\text{P}}{{\text{O}}_{\text{4}}}\), formed in the reaction.
Phosphoric(V) acid, \({{\text{H}}_{\text{3}}}{\text{P}}{{\text{O}}_{\text{4}}}\), has a \({\text{p}}{K_{\text{a}}}\) of 2.12 (\({\text{p}}{K_{{\text{a1}}}}\)) while phosphoric(III) acid, \({{\text{H}}_{\text{3}}}{\text{P}}{{\text{O}}_{\text{3}}}\), has a \({\text{p}}{K_{\text{a}}}\) of 1.23 (\({\text{p}}{K_{{\text{a1}}}}\)). Identify the weaker of the two acids, giving a reason for your choice.
Water is an important substance that is abundant on the Earth’s surface.
Buffer solutions resist small changes in pH. A phosphate buffer can be made by dissolving \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) in water, in which \({\text{Na}}{{\text{H}}_{\text{2}}}{\text{P}}{{\text{O}}_{\text{4}}}\) produces the acidic ion and \({\text{N}}{{\text{a}}_{\text{2}}}{\text{HP}}{{\text{O}}_{\text{4}}}\) produces the conjugate base ion.
A \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) ammonia solution is placed in a flask and titrated with a \({\text{0.10 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid solution.
(i) State the expression for the ionic product constant of water, \({K_{\text{w}}}\).
(ii) Explain why even a very acidic aqueous solution still has some \({\text{O}}{{\text{H}}^ - }\) ions present in it.
(iii) State and explain the effect of increasing temperature on the value of \({K_{\text{w}}}\) given that the ionization of water is an endothermic process.
(iv) State and explain the effect of increasing temperature on the pH of water.
(i) Deduce the acid and conjugate base ions that make up the phosphate buffer and state the ionic equation that represents the phosphate buffer.
(ii) Describe how the phosphate buffer minimizes the effect of the addition of a
strong base, \({\text{O}}{{\text{H}}^ - }{\text{(aq)}}\), to the buffer. Illustrate your answer with an ionic equation.
(iii) Describe how the phosphate buffer minimizes the effect of the addition of a
strong acid, \({{\text{H}}^ + }{\text{(aq)}}\), to the buffer. Illustrate your answer with an ionic equation.
(i) Explain why the pH of the ammonia solution is less than 13.
(ii) Estimate the pH at the equivalence point for the titration of hydrochloric acid with ammonia and explain your reasoning.
(iii) State the equation for the reaction of ammonia with water and write the \({K_{\text{b}}}\) expression for \({\text{N}}{{\text{H}}_{\text{3}}}{\text{(aq)}}\).
(iv) When half the ammonia has been neutralized (the half-equivalence point), the pH of the solution is 9.25. Deduce the relationship between \({\text{[N}}{{\text{H}}_{\text{3}}}{\text{]}}\) and \({\text{[NH}}_4^ + {\text{]}}\) at the
half-equivalence point.
(v) Determine \({\text{p}}{K_{\text{b}}}\) and \({K_{\text{b}}}\) for ammonia based on the pH at the half-equivalence point.
(vi) Describe the significance of the half-equivalence point in terms of its effectiveness as a buffer.
Buffer solutions are widely used in both chemical and biochemical systems.
Describe the composition of an acidic buffer solution.
Determine the pH of a buffer solution, correct to two decimal places, showing your working, consisting of 10.0 g of \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH}}\) and 10.0 g of CH\(_3\)COONa in \({\text{0.250 d}}{{\text{m}}^{\text{3}}}\) of solution. \({K_{\text{a}}}\) for \({\text{C}}{{\text{H}}_{\text{3}}}{\text{COOH}} = 1.8 \times {10^{ - 5}}\) at 298 K.
Titanium and vanadium are consecutive elements in the first transition metal series.
\({\text{TiC}}{{\text{l}}_{\text{4}}}\) reacts with water and the resulting titanium(IV) oxide can be used as a smoke screen.
Describe the bonding in metals.
Titanium exists as several isotopes. The mass spectrum of a sample of titanium gave the following data:
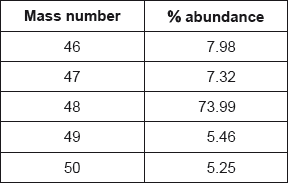
Calculate the relative atomic mass of titanium to two decimal places.
State the number of protons, neutrons and electrons in the \(_{{\text{22}}}^{{\text{48}}}{\text{Ti}}\) atom.

State the full electron configuration of the \(_{{\text{22}}}^{{\text{48}}}{\text{T}}{{\text{i}}^{2 + }}\) ion.
Suggest why the melting point of vanadium is higher than that of titanium.
Sketch a graph of the first six successive ionization energies of vanadium on the axes provided.
Explain why an aluminium-titanium alloy is harder than pure aluminium.
Describe, in terms of the electrons involved, how the bond between a ligand and a central metal ion is formed.
Outline why transition metals form coloured compounds.
State the type of bonding in potassium chloride which melts at 1043 K.
A chloride of titanium, \({\text{TiC}}{{\text{l}}_{\text{4}}}\), melts at 248 K. Suggest why the melting point is so much lower than that of KCl.
Formulate an equation for this reaction.
Suggest one disadvantage of using this smoke in an enclosed space.
Soluble acids and bases ionize in water.
A solution containing 0.510 g of an unknown monoprotic acid, HA, was titrated with 0.100 mol dm–3 NaOH(aq). 25.0 cm3 was required to reach the equivalence point.
The following curve was obtained using a pH probe.
State, giving a reason, the strength of the acid.
State a technique other than a pH titration that can be used to detect the equivalence point.
Deduce the pKa for this acid.
The pKa of an anthocyanin is 4.35. Determine the pH of a 1.60 × 10–3 mol dm–3 solution to two decimal places.
This question is about the weak acid methanoic acid, HCOOH.
Calculate the pH of 0.0100 mol dm–3 methanoic acid stating any assumption you make. Ka = 1.6 × 10–4.
(i) Sketch a graph of pH against volume of a strong base added to a weak acid showing how you would determine pKa for the weak acid.
(ii) Explain, using an equation, why the pH increases very little in the buffer region when a small amount of alkali is added.
Chromium is a transition metal with many uses.
A voltaic cell is constructed as follows. One half-cell contains a chromium electrode immersed in a solution containing \({\text{C}}{{\text{r}}^{3 + }}{\text{(aq)}}\) ions. The other half-cell contains a copper electrode immersed in a solution containing \({\text{C}}{{\text{u}}^{2 + }}{\text{(aq)}}\) ions. The two electrodes are connected to a voltmeter and the two solutions by a salt bridge.
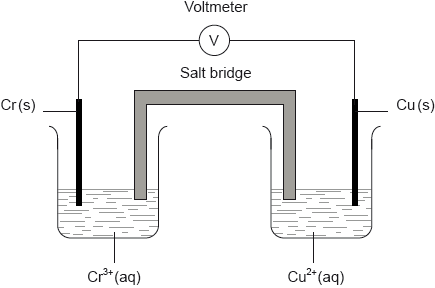
Draw an orbital diagram (using the arrow-in-box notation) showing the electrons in the 4s and 3d sub-levels in chromium metal.
Outline the nature of the metallic bonding present in chromium.
Explain why chromium metal is malleable.
State the name of \({\text{C}}{{\text{r}}_{\text{2}}}{{\text{O}}_{\text{3}}}\).
Describe the ionic bonding present in \({\text{C}}{{\text{r}}_{\text{2}}}{{\text{O}}_{\text{3}}}\) and how the ions are formed.
Suggest why solid \({\text{C}}{{\text{r}}_{\text{2}}}{{\text{O}}_{\text{3}}}\) does not conduct electricity.
Chromium forms the complex ion \({[{\text{Cr}}{({\text{N}}{{\text{H}}_{\text{3}}})_{\text{4}}}{\text{C}}{{\text{l}}_2}]^ + }\).
Deduce the oxidation number of chromium in this complex.
Chromium forms the complex ion \({[{\text{Cr}}{({\text{N}}{{\text{H}}_{\text{3}}})_{\text{4}}}{\text{C}}{{\text{l}}_2}]^ + }\).
Describe the nature of the ligand-chromium ion bonds in terms of acid-base theory.
Chromium forms the complex ion \({[{\text{Cr}}{({\text{N}}{{\text{H}}_{\text{3}}})_{\text{4}}}{\text{C}}{{\text{l}}_2}]^ + }\).
Explain why \({[{\text{Cr}}{({\text{N}}{{\text{H}}_{\text{3}}})_{\text{4}}}{\text{C}}{{\text{l}}_{\text{2}}}{\text{]}}^ + }\) is coloured.
Chromium forms the complex ion \({[{\text{Cr}}{({\text{N}}{{\text{H}}_{\text{3}}})_{\text{4}}}{\text{C}}{{\text{l}}_2}]^ + }\).
Draw the structures of two possible isomers of this complex ion.
The dichromate ion, \({\text{C}}{{\text{r}}_{\text{2}}}{\text{O}}_{\text{7}}^{2 - }{\text{(aq)}}\), and the iodide ion, \({{\text{I}}^ - }{\text{(aq)}}\), react together in the presence of an acid to form \({\text{C}}{{\text{r}}^{3 + }}{\text{(aq)}}\) and \({\text{IO}}_3^ - {\text{(aq)}}\) ions. Deduce the half-equation for the reaction of \({{\text{I}}^ - }\) to \({\text{IO}}_3^ - \) and the overall equation for this reaction.
Half-equation:
Overall equation:
Explain in terms of oxidation numbers whether iodine is oxidized or reduced in part (d) (i).
Define the term standard electrode potential.
Calculate the cell potential, in V, under standard conditions, for this voltaic cell, using table 14 of the data booklet and \({\text{E}}_{{\text{C}}{{\text{r}}^{3 + }}/{\text{Cr}}}^\Theta = -0.74{\text{ V}}\).
Predict the balanced equation for the spontaneous reaction which will produce a current in this voltaic cell.
Identify the negative and the positive electrodes in this cell.
Predict the direction of movement of electrons in the external circuit.
State the directions in which the negative ions (anions) and the positive ions (cations) flow in the salt bridge.
Phosphine (IUPAC name phosphane) is a hydride of phosphorus, with the formula PH3.
(i) Draw a Lewis (electron dot) structure of phosphine.
(ii) State the hybridization of the phosphorus atom in phosphine.
(iii) Deduce, giving your reason, whether phosphine would act as a Lewis acid, a Lewis base, or neither.
(iv) Outline whether you expect the bonds in phosphine to be polar or non-polar, giving a brief reason.
(v) Phosphine has a much greater molar mass than ammonia. Explain why phosphine has a significantly lower boiling point than ammonia.
(vi) Ammonia acts as a weak Brønsted–Lowry base when dissolved in water.
Outline what is meant by the terms “weak” and “Brønsted–Lowry base”.
Weak:
Brønsted–Lowry base:
Phosphine is usually prepared by heating white phosphorus, one of the allotropes of phosphorus, with concentrated aqueous sodium hydroxide. The equation for the reaction is:
(i) The first reagent is written as P4, not 4P. Describe the difference between P4 and 4P.
(ii) The ion H2PO2− is amphiprotic. Outline what is meant by amphiprotic, giving the formulas of both species it is converted to when it behaves in this manner.
(iii) State the oxidation state of phosphorus in P4 and H2PO2−.
P4:
H2PO2−:
(iv) Oxidation is now defined in terms of change of oxidation number. Explore how earlier definitions of oxidation and reduction may have led to conflicting answers for the conversion of P4 to H2PO2− and the way in which the use of oxidation numbers has resolved this.
2.478 g of white phosphorus was used to make phosphine according to the equation:
(i) Calculate the amount, in mol, of white phosphorus used.
(ii) This phosphorus was reacted with 100.0 cm3 of 5.00 mol dm−3 aqueous sodium hydroxide. Deduce, showing your working, which was the limiting reagent.
(iii) Determine the excess amount, in mol, of the other reagent.
(iv) Determine the volume of phosphine, measured in cm3 at standard temperature and pressure, that was produced.
Impurities cause phosphine to ignite spontaneously in air to form an oxide of phosphorus and water.
(i) 200.0 g of air was heated by the energy from the complete combustion of 1.00 mol phosphine. Calculate the temperature rise using section 1 of the data booklet and the data below.
Standard enthalpy of combustion of phosphine,
Specific heat capacity of air = 1.00Jg−1K−1=1.00kJkg−1K−1
(ii) The oxide formed in the reaction with air contains 43.6% phosphorus by mass. Determine the empirical formula of the oxide, showing your method.
(iii) The molar mass of the oxide is approximately 285 g mol−1. Determine the molecular formula of the oxide.
(iv) State the equation for the reaction of this oxide of phosphorus with water.
(v) Suggest why oxides of phosphorus are not major contributors to acid deposition.
(vi) The levels of sulfur dioxide, a major contributor to acid deposition, can be minimized by either pre-combustion and post-combustion methods. Outline one technique of each method.
Pre-combustion:
Post-combustion:
Phosgene, COCl2, is usually produced by the reaction between carbon monoxide and chlorine according to the equation:
(i) Deduce the equilibrium constant expression, Kc, for this reaction.
(ii) At exactly 600°C the value of the equilibrium constant is 0.200. Calculate the standard Gibbs free energy change, , for the reaction, in kJ, using sections 1 and 2 of the data booklet. State your answer to three significant figures.
(iii) The standard enthalpy change of formation of phosgene, \(\Delta H_f^\Theta \), is −220.1kJmol−1. Determine the standard enthalpy change, \(\Delta H_{}^\Theta \), for the forward reaction of the equilibrium, in kJ, using section 12 of the data booklet.
(iv) Calculate the standard entropy change, \(\Delta S_{}^\Theta \), in JK−1, for the forward reaction at 25°C, using your answers to (a) (ii) and (a) (iii). (If you did not obtain an answer to (a) (ii) and/or (a) (iii) use values of +20.0 kJ and −120.0 kJ respectively, although these are not the correct answers.)
One important industrial use of phosgene is the production of polyurethanes. Phosgene is reacted with diamine X, derived from phenylamine.
(i) Classify diamine X as a primary, secondary or tertiary amine.
(ii) Phenylamine, C6H5NH2, is produced by the reduction of nitrobenzene, C6H5NO2. Suggest how this conversion can be carried out.
(iii) Nitrobenzene can be obtained by nitrating benzene using a mixture of concentrated nitric and sulfuric acids. Formulate the equation for the equilibrium established when these two acids are mixed.
(iv) Deduce the mechanism for the nitration of benzene, using curly arrows to indicate the movement of electron pairs.
The other monomer used in the production of polyurethane is compound Z shown below.
(i) State the name, applying IUPAC rules, of compound Z and the class of compounds to which it belongs.
Name:
Class:
(ii) Deduce the number of signals you would expect to find in the 1H NMR spectrum of compound Z, giving your reasons.
The mass spectrum and infrared (IR) spectrum of compound Z are shown below:
Mass spectrum
IR spectrum
(iii) Identify the species causing the large peak at m/z=31 in the mass spectrum.
(iv) Identify the bond that produces the peak labelled Q on the IR spectrum, using section 26 of the data booklet.
Phenylamine can act as a weak base. Calculate the pH of a 0.0100 mol dm−3 solution of phenylamine at 298K using section 21 of the data booklet.