
HL Paper 2
The graph of \(y = \ln (5x + 10)\) is obtained from the graph of \(y = \ln x\) by a translation of \(a\) units in the direction of the \(x\)-axis followed by a translation of \(b\) units in the direction of the \(y\)-axis.
Find the value of \(a\) and the value of \(b\).
The region bounded by the graph of \(y = \ln (5x + 10)\), the \(x\)-axis and the lines \(x = {\text{e}}\) and \(x = 2{\text{e}}\), is rotated through \(2\pi \) radians about the \(x\)-axis. Find the volume generated.
Markscheme
EITHER
\(y = \ln (x - a) + b = \ln (5x + 10)\) (M1)
\(y = \ln (x - a) + \ln c = \ln (5x + 10)\)
\(y = \ln \left( {c(x - a)} \right) = \ln (5x + 10)\) (M1)
OR
\(y = \ln (5x + 10) = \ln \left( {5(x + 2)} \right)\) (M1)
\(y = \ln (5) + \ln (x + 2)\) (M1)
THEN
\(a = - 2,{\text{ }}b = \ln 5\) A1A1
Note: Accept graphical approaches.
Note: Accept \(a = 2,{\text{ }}b = 1.61\)
[4 marks]
\(V = \pi {\int_e^{2e} {\left[ {\ln (5x + 10)} \right]} ^2}{\text{d}}x\) (M1)
\( = 99.2\) A1
[2 marks]
Total [6 marks]
Examiners report
Consider \(p(x) = 3{x^3} + ax + 5a,\;\;\;a \in \mathbb{R}\).
The polynomial \(p(x)\) leaves a remainder of \( - 7\) when divided by \((x - a)\).
Show that only one value of \(a\) satisfies the above condition and state its value.
Markscheme
using \(p(a) = - 7\) to obtain \(3{a^3} + {a^2} + 5a + 7 = 0\) M1A1
\((a + 1)(3{a^3} - 2a + 7) = 0\) (M1)(A1)
Note: Award M1 for a cubic graph with correct shape and A1 for clearly showing that the above cubic crosses the horizontal axis at \(( - 1,{\text{ }}0)\) only.
\(a = - 1\) A1
EITHER
showing that \(3{a^2} - 2a + 7 = 0\) has no real (two complex) solutions for \(a\) R1
OR
showing that \(3{a^3} + {a^2} + 5a + 7 = 0\) has one real (and two complex) solutions for \(a\) R1
Note: Award R1 for solutions that make specific reference to an appropriate graph.
[6 marks]
Examiners report
A large number of candidates, either by graphical (mostly) or algebraic or via use of a GDC solver, were able to readily obtain \(a = - 1\). Most candidates who were awarded full marks however, made specific reference to an appropriate graph. Only a small percentage of candidates used the discriminant to justify that only one value of \(a\) satisfied the required condition. A number of candidates erroneously obtained \(3{a^3} + {a^2} + 5a - 7 = 0\) or equivalent rather than \(3{a^3} + {a^2} + 5a + 7 = 0\).
Find \(\int {x{{\sec }^2}x{\text{d}}x} \).
Determine the value of m if \(\int_0^m {x{{\sec }^2}x{\text{d}}x = 0.5} \), where m > 0.
Markscheme
\(\int {x{{\sec }^2}x{\text{d}}x} = x\tan x - \int {1 \times \tan x{\text{d}}x} \) M1A1
\( = x\tan x + \ln \left| {\cos x} \right|( + c){\text{ }}\left( { = x\tan x - \ln \left| {\sec x} \right|( + c)} \right)\) M1A1
[4 marks]
attempting to solve an appropriate equation eg \(m\tan m + \ln (\cos m) = 0.5\) (M1)
m = 0.822 A1
Note: Award A1 if m = 0.822 is specified with other positive solutions.
[2 marks]
Examiners report
In part (a), a large number of candidates were able to use integration by parts correctly but were unable to use integration by substitution to then find the indefinite integral of tan x. In part (b), a large number of candidates attempted to solve the equation without direct use of a GDC’s numerical solve command. Some candidates stated more than one solution for m and some specified m correct to two significant figures only.
In part (a), a large number of candidates were able to use integration by parts correctly but were unable to use integration by substitution to then find the indefinite integral of tan x. In part (b), a large number of candidates attempted to solve the equation without direct use of a GDC’s numerical solve command. Some candidates stated more than one solution for m and some specified m correct to two significant figures only.
It is given that \(f(x) = 3{x^4} + a{x^3} + b{x^2} - 7x - 4\) where \(a\) and \(b\) are positive integers.
Given that \({x^2} - 1\) is a factor of \(f(x)\) find the value of \(a\) and the value of \(b\).
Factorize \(f(x)\) into a product of linear factors.
Sketch the graph of \(y = f(x)\), labelling the maximum and minimum points and the \(x\) and \(y\) intercepts.
Using your graph state the range of values of \(c\) for which \(f(x) = c\) has exactly two distinct real roots.
Markscheme
\(g(x) = 3{x^4} + a{x^3} + b{x^2} - 7x - 4\)
\(g(1) = 0 \Rightarrow a + b = 8\) M1A1
\(g( - 1) = 0 \Rightarrow - a + b = - 6\) A1
\( \Rightarrow a = 7,{\text{ }}b = 1\) A1
[4 marks]
\(3{x^4} + 7{x^3} + {x^2} - 7x - 4 = ({x^2} - 1)(p{x^2} + qx + r)\)
attempt to equate coefficients (M1)
\(p = 3,{\text{ }}q = 7,{\text{ }}r = 4\) (A1)
\(3{x^4} + 7{x^3} + {x^2} - 7x - 4 = ({x^2} - 1)(3{x^2} + 7x + 4)\)
\( = (x - 1){(x + 1)^2}(3x + 4)\) A1
Note: Accept any equivalent valid method.
[3 marks]
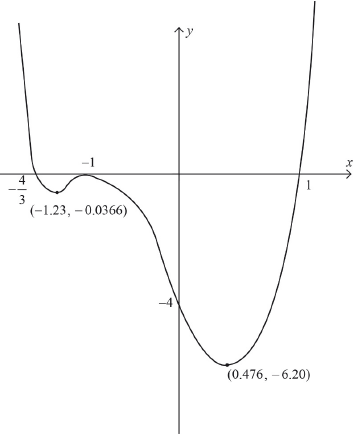
A1 for correct shape (ie with correct number of max/min points)
A1 for correct \(x\) and \(y\) intercepts
A1 for correct maximum and minimum points
[3 marks]
\(c > 0\) A1
\( - 6.20 < c < - 0.0366\) A1A1
Note: Award A1 for correct end points and A1 for correct inequalities.
Note: If the candidate has misdrawn the graph and omitted the first minimum point, the maximum mark that may be awarded is A1FTA0A0 for \(c > - 6.20\) seen.
[3 marks]
Examiners report
The function \(f(x) = 3\sin x + 4\cos x\) is defined for \(0 < x < 2\pi \) .
Write down the coordinates of the minimum point on the graph of f .
The points \({\text{P}}(p,{\text{ }}3)\) and \({\text{Q}}(q,{\text{ }}3){\text{, }}q > p\), lie on the graph of \(y = f(x)\) .
Find p and q .
Find the coordinates of the point, on \(y = f(x)\) , where the gradient of the graph is 3.
Find the coordinates of the point of intersection of the normals to the graph at the points P and Q.
Markscheme
\((3.79, - 5)\) A1
[1 mark]
\(p = 1.57{\text{ or }}\frac{\pi }{2},{\text{ }}q = 6.00\) A1A1
[2 marks]
\(f'(x) = 3\cos x - 4\sin x\) (M1)(A1)
\(3\cos x - 4\sin x = 3 \Rightarrow x = 4.43...\) (A1)
\((y = -4)\) A1
Coordinates are \((4.43, -4)\)
[4 marks]
\({m_{{\text{normal}}}} = \frac{1}{{{m_{{\text{tangent}}}}}}\) (M1)
gradient at P is \( - 4\) so gradient of normal at P is \(\frac{1}{4}\) (A1)
gradient at Q is 4 so gradient of normal at Q is \( - \frac{1}{4}\) (A1)
equation of normal at P is \(y - 3 = \frac{1}{4}(x - 1.570...){\text{ }}({\text{or }}y = 0.25x + 2.60...)\) (M1)
equation of normal at Q is \(y - 3 = \frac{1}{4}(x - 5.999...){\text{ }}({\text{or }}y = -0.25x + \underbrace {4.499...}_{})\) (M1)
Note: Award the previous two M1 even if the gradients are incorrect in \(y - b = m(x - a)\) where \((a,b)\) are coordinates of P and Q (or in \(y = mx + c\) with c determined using coordinates of P and Q.
intersect at \((3.79,{\text{ }}3.55)\) A1A1
Note: Award N2 for 3.79 without other working.
[7 marks]
Examiners report
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Candidates answered parts (a) and (b) of this question well and, although many were also successful in part (c), just a few candidates gave answers to the required level of accuracy. Part d) was rather challenging for many candidates. The most common errors among the candidates who attempted this question were the confusion between tangents and normals and incorrect final answers due to premature rounding.
Show that the quadratic equation \({x^2} - (5 - k)x - (k + 2) = 0\) has two distinct real roots for all real values of k .
Markscheme
\(\Delta = {(5 - k)^2} + 4(k + 2)\) M1A1
\( = {k^2} - 6k + 33\) (A1)
\( = {(k - 3)^2} + 24\) which is positive for all k R1
Note: Accept analytical, graphical or other correct methods. In all cases only award R1 if a reason is given in words or graphically. Award M1A1A0R1 if mistakes are made in the simplification but the argument given is correct.
[4 marks]
Examiners report
Overall the question was pretty well answered but some candidates seemed to have mixed up the terms determinant with discriminant. In some cases a lack of quality mathematical reasoning and understanding of the discriminant was evident. Many worked with the quadratic formula rather than just the discriminant, conveying a lack of understanding of the strategy required. Errors in algebraic simplification (expanding terms involving negative signs) prevented many candidates from scoring well in this question. Many candidates were not able to give a clear reason why the quadratic has always two distinct real solutions; in some cases a vague explanation was given, often referring to a graph which was not sketched.
Express \({x^2} + 4x - 2\) in the form \({(x + a)^2} + b\) where \(a,{\text{ }}b \in \mathbb{Z}\).
If \(f(x) = x + 2\) and \((g \circ f)(x) = {x^2} + 4x - 2\) write down \(g(x)\).
Markscheme
\({(x + 2)^2} - 6\) A1A1
[2 marks]
\((g \circ f)(x) = {(x + 2)^2} - 6\) (M1)
\( \Rightarrow g(x) = {x^2} - 6\) A1
[2 marks]
Examiners report
Well done by most candidates.
Well done by most candidates. Those students who lost marks on this question tended to do so in part (b), seemingly through misinterpreting the question.
The following graph represents a function \(y = f(x)\), where \( - 3 \le x \le 5\).
The function has a maximum at \((3,{\text{ }}1)\) and a minimum at \(( - 1,{\text{ }} - 1)\).
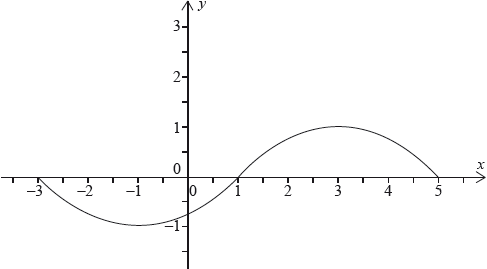
The functions \(u\) and \(v\) are defined as \(u(x) = x - 3,{\text{ }}v(x) = 2x\) where \(x \in \mathbb{R}\).
(i) State the range of the function \(u \circ f\).
(ii) State the range of the function \(u \circ v \circ f\).
(iii) Find the largest possible domain of the function \(f \circ v \circ u\).
(i) Explain why \(f\) does not have an inverse.
(ii) The domain of \(f\) is restricted to define a function \(g\) so that it has an inverse \({g^{ - 1}}\).
State the largest possible domain of \(g\).
(iii) Sketch a graph of \(y = {g^{ - 1}}(x)\), showing clearly the \(y\)-intercept and stating the coordinates of the endpoints.
Consider the function defined by \(h(x) = \frac{{2x - 5}}{{x + d}}\), \(x \ne - d\) and \(d \in \mathbb{R}\).
(i) Find an expression for the inverse function \({h^{ - 1}}(x)\).
(ii) Find the value of \(d\) such that \(h\) is a self-inverse function.
For this value of \(d\), there is a function \(k\) such that \(h \circ k(x) = \frac{{2x}}{{x + 1}},{\text{ }}x \ne - 1\).
(iii) Find \(k(x)\).
Markscheme
Note: For Q12(a) (i) – (iii) and (b) (ii), award A1 for correct endpoints and, if correct, award A1 for a closed interval.
Further, award A1A0 for one correct endpoint and a closed interval.
(i) \( - 4 \le y \le - 2\) A1A1
(ii) \( - 5 \le y \le - 1\) A1A1
(iii) \( - 3 \le 2x - 6 \le 5\) (M1)
Note: Award M1 for \(f(2x - 6)\).
\(3 \le 2x \le 11\)
\(\frac{3}{2} \le x \le \frac{{11}}{2}\) A1A1
[7 marks]
(i) any valid argument eg \(f\) is not one to one, \(f\) is many to one, fails horizontal line test, not injective R1
(ii) largest domain for the function \(g(x)\) to have an inverse is \([ - 1,{\text{ }}3]\) A1A1
(iii) 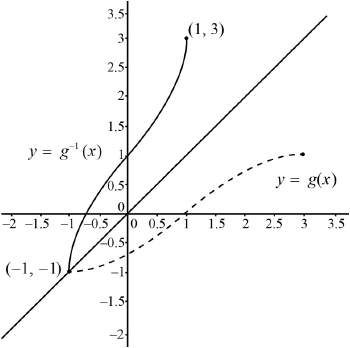
\(y\)-intercept indicated (coordinates not required) A1
correct shape A1
coordinates of end points \((1,{\text{ }}3)\) and \(( - 1,{\text{ }} - 1)\) A1
Note: Do not award any of the above marks for a graph that is not one to one.
[6 marks]
(i) \(y = \frac{{2x - 5}}{{x + d}}\)
\((x + d)y = 2x - 5\) M1
Note: Award M1 for attempting to rearrange \(x\) and \(y\) in a linear expression.
\(x(y - 2) = - dy - 5\) (A1)
\(x = \frac{{ - dy - 5}}{{y - 2}}\) (A1)
Note: \(x\) and \(y\) can be interchanged at any stage
\({h^{ - 1}}(x) = \frac{{ - dx - 5}}{{x - 2}}\) A1
Note: Award A1 only if \({h^{ - 1}}(x)\) is seen.
(ii) self Inverse \( \Rightarrow h(x) = {h^{ - 1}}(x)\)
\(\frac{{2x - 5}}{{x + d}} \equiv \frac{{ - dx - 5}}{{x - 2}}\) (M1)
\(d = - 2\) A1
(iii) METHOD 1
\(\frac{{2k(x) - 5}}{{k(x) - 2}} = \frac{{2x}}{{x + 1}}\) (M1)
\(k(x) = \frac{{x + 5}}{2}\) A1
METHOD 2
\({h^{ - 1}}\left( {\frac{{2x}}{{x + 1}}} \right) = \frac{{2\left( {\frac{{2x}}{{x + 1}}} \right) - 5}}{{\frac{{2x}}{{x + 1}} - 2}}\) (M1)
\(k(x) = \frac{{x + 5}}{2}\) A1
[8 marks]
Total [21 marks]
Examiners report
The function f has inverse \({f^{ - 1}}\) and derivative \(f'(x)\) for all \(x \in \mathbb{R}\). For all functions with these properties you are given the result that for \(a \in \mathbb{R}\) with \(b = f(a)\) and \(f'(a) \ne 0\)
\[({f^{ - 1}})'(b) = \frac{1}{{f'(a)}}.\]
Verify that this is true for \(f(x) = {x^3} + 1\) at x = 2.
Given that \(g(x) = x{{\text{e}}^{{x^2}}}\), show that \(g'(x) > 0\) for all values of x.
Using the result given at the start of the question, find the value of the gradient function of \(y = {g^{ - 1}}(x)\) at x = 2.
(i) With f and g as defined in parts (a) and (b), solve \(g \circ f(x) = 2\).
(ii) Let \(h(x) = {(g \circ f)^{ - 1}}(x)\). Find \(h'(2)\).
Markscheme
\(f(2) = 9\) (A1)
\({f^{ - 1}}(x) = {(x - 1)^{\frac{1}{3}}}\) A1
\(({f^{ - 1}})'(x) = \frac{1}{3}{(x - 1)^{ - \frac{2}{3}}}\) (M1)
\(({f^{ - 1}})'(9) = \frac{1}{{12}}\) A1
\(f'(x) = 3{x^2}\) (M1)
\(\frac{1}{{f'(2)}} = \frac{1}{{3 \times 4}} = \frac{1}{{12}}\) A1
Note: The last M1 and A1 are independent of previous marks.
[6 marks]
\(g'(x) = {{\text{e}}^{{x^2}}} + 2{x^2}{{\text{e}}^{{x^2}}}\) M1A1
\(g'(x) > 0\) as each part is positive R1
[3 marks]
to find the x-coordinate on \(y = g(x)\) solve
\(2 = x{{\text{e}}^{{x^2}}}\) (M1)
\(x = 0.89605022078 \ldots \) (A1)
gradient \( = ({g^{ - 1}})'(2) = \frac{1}{{g'(0.896 \ldots )}}\) (M1)
\( = \frac{1}{{{{\text{e}}^{{{(0.896 \ldots )}^2}}}\left( {1 + 2 \times {{(0.896 \ldots )}^2}} \right)}} = 0.172\) to 3sf A1
(using the \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) function on gdc \(g'(0.896 \ldots ) = 5.7716028 \ldots \)
\(\frac{1}{{g'(0.896 \ldots )}} = 0.173\)
[4 marks]
(i) \(({x^3} + 1){{\text{e}}^{{{({x^3} + 1)}^2}}} = 2\) A1
\(x = - 0.470191 \ldots \) A1
(ii) METHOD 1
\((g \circ f)'(x) = 3{x^2}{{\text{e}}^{{{({x^3} + 1)}^2}}}\left( {2{{({x^3} + 1)}^2} + 1} \right)\) (M1)(A1)
\((g \circ f)'( - 0.470191 \ldots ) = 3.85755 \ldots \) (A1)
\(h'(2) = \frac{1}{{3.85755 \ldots }} = 0.259{\text{ }}(232 \ldots )\) A1
Note: The solution can be found without the student obtaining the explicit form of the composite function.
METHOD 2
\(h(x) = ({f^{ - 1}} \circ {g^{ - 1}})(x)\) A1
\(h'(x) = ({f^{ - 1}})'\left( {{g^{ - 1}}(x)} \right) \times ({g^{ - 1}})'(x)\) M1
\( = \frac{1}{3}{\left( {{g^{ - 1}}(x) - 1} \right)^{ - \frac{2}{3}}} \times ({g^{ - 1}})'(x)\) M1
\(h'(2) = \frac{1}{3}{\left( {{g^{ - 1}}(2) - 1} \right)^{ - \frac{2}{3}}} \times ({g^{ - 1}})'(2)\)
\( = \frac{1}{3}{(0.89605 \ldots - 1)^{ - \frac{2}{3}}} \times 0.171933 \ldots \)
\( = 0.259{\text{ }}(232 \ldots )\) A1 N4
[6 marks]
Examiners report
There were many good attempts at parts (a) and (b), although in (b) many were unable to give a thorough justification.
There were many good attempts at parts (a) and (b), although in (b) many were unable to give a thorough justification.
Few good solutions to parts (c) and (d)(ii) were seen although many were able to answer (d)(i) correctly.
Few good solutions to parts (c) and (d)(ii) were seen although many were able to answer (d)(i) correctly.
Let \(f(x) = x{(x + 2)^6}\).
Solve the inequality \(f(x) > x\).
Find \(\int {f(x){\text{d}}x} \).
Markscheme
METHOD 1
sketch showing where the lines cross or zeros of \(y = x{(x + 2)^6} - x\) (M1)
\(x = 0\) (A1)
\(x = - 1\) and \(x = - 3\) (A1)
the solution is \( - 3 < x < - 1\) or \(x > 0\) A1A1
Note: Do not award either final A1 mark if strict inequalities are not given.
METHOD 2
separating into two cases \(x > 0\) and \(x < 0\) (M1)
if \(x > 0\) then \({(x + 2)^6} > 1 \Rightarrow \) always true (M1)
if \(x < 0\) then \({(x + 2)^6} < 1 \Rightarrow - 3 < x < - 1\) (M1)
so the solution is \( - 3 < x < - 1\) or \(x > 0\) A1A1
Note: Do not award either final A1 mark if strict inequalities are not given.
METHOD 3
\(f(x) = {x^7} + 12{x^6} + 60{x^5} + 160{x^4} + 240{x^3} + 192{x^2} + 64x\) (A1)
solutions to \({x^7} + 12{x^6} + 60{x^5} + 160{x^4} + 240{x^3} + 192{x^2} + 63x = 0\) are (M1)
\(x = 0,{\text{ }}x = - 1\) and \(x = - 3\) (A1)
so the solution is \( - 3 < x < - 1\) or \(x > 0\) A1A1
Note: Do not award either final A1 mark if strict inequalities are not given.
METHOD 4
\(f(x) = x\) when \(x{(x + 2)^6} = x\)
either \(x = 0\) or \({(x + 2)^6} = 1\) (A1)
if \({(x + 2)^6} = 1\) then \(x + 2 = \pm 1\) so \(x = - 1\) or \(x = - 3\) (M1)(A1)
the solution is \( - 3 < x < - 1\) or \(x > 0\) A1A1
Note: Do not award either final A1 mark if strict inequalities are not given.
[5 marks]
METHOD 1 (by substitution)
substituting \(u = x + 2\) (M1)
\({\text{d}}u = {\text{d}}x\)
\(\int {(u - 2){u^6}{\text{d}}u} \) M1A1
\( = \frac{1}{8}{u^8} - \frac{2}{7}{u^7}( + c)\) (A1)
\( = \frac{1}{8}{(x + 2)^8} - \frac{2}{7}{(x + 2)^7}( + c)\) A1
METHOD 2 (by parts)
\(u = x \Rightarrow \frac{{{\text{d}}u}}{{{\text{d}}x}} = 1,{\text{ }}\frac{{{\text{d}}v}}{{{\text{d}}x}} = {(x + 2)^6} \Rightarrow v = \frac{1}{7}{(x + 2)^7}\) (M1)(A1)
\(\int {x{{(x + 2)}^6}{\text{d}}x = \frac{1}{7}x{{(x + 2)}^7} - \frac{1}{7}\int {{{(x + 2)}^7}{\text{d}}x} } \) M1
\( = \frac{1}{7}x{(x + 2)^7} - \frac{1}{{56}}{(x + 2)^8}( + c)\) A1A1
METHOD 3 (by expansion)
\(\int {f(x){\text{d}}x = \int {\left( {{x^7} + 12{x^6} + 60{x^5} + 160{x^4} + 240{x^3} + 192{x^2} + 64x} \right){\text{d}}x} } \) M1A1
\( = \frac{1}{8}{x^8} + \frac{{12}}{7}{x^7} + 10{x^6} + 32{x^5} + 60{x^4} + 64{x^3} + 32{x^2}( + c)\) M1A2
Note: Award M1A1 if at least four terms are correct.
[5 marks]
Examiners report
One root of the equation \({x^2} + ax + b = 0\) is \(2 + 3{\text{i}}\) where \(a,{\text{ }}b \in \mathbb{R}\). Find the value of \(a\) and the value of \(b\).
Markscheme
METHOD 1
substituting
\( - 5 + 12{\text{i}} + a(2 + 3{\text{i}}) + b = 0\) (A1)
equating real or imaginary parts (M1)
\(12 + 3a = 0 \Rightarrow a = - 4\) A1
\( - 5 + 2a + b = 0 \Rightarrow b = 13\) A1
METHOD 2
other root is \(2 - 3{\text{i}}\) (A1)
considering either the sum or product of roots or multiplying factors (M1)
\(4 = - a\) (sum of roots) so \(a = - 4\) A1
\(13 = b\) (product of roots) A1
[4 marks]
Examiners report
The polynomial \({x^4} + p{x^3} + q{x^2} + rx + 6\) is exactly divisible by each of \(\left( {x - 1} \right)\), \(\left( {x - 2} \right)\) and \(\left( {x - 3} \right)\).
Find the values of \(p\), \(q\) and \(r\).
Markscheme
METHOD 1
substitute each of \(x\) = 1,2 and 3 into the quartic and equate to zero (M1)
\(p + q + r = - 7\)
\(4p + 2q + r = - 11\) or equivalent (A2)
\(9p + 3q + r = - 29\)
Note: Award A2 for all three equations correct, A1 for two correct.
attempting to solve the system of equations (M1)
\(p\) = −7, \(q\) = 17, \(r\) = −17 A1
Note: Only award M1 when some numerical values are found when solving algebraically or using GDC.
METHOD 2
attempt to find fourth factor (M1)
\(\left( {x - 1} \right)\) A1
attempt to expand \({\left( {x - 1} \right)^2}\left( {x - 2} \right)\left( {x - 3} \right)\) M1
\({x^4} - 7{x^3} + 17{x^2} - 17x + 6\) (\(p\) = −7, \(q\) = 17, \(r\) = −17) A2
Note: Award A2 for all three values correct, A1 for two correct.
Note: Accept long / synthetic division.
[5 marks]
Examiners report
A function \(f\) is defined by \(f(x) = {x^3} + {{\text{e}}^x} + 1,{\text{ }}x \in \mathbb{R}\). By considering \(f'(x)\) determine whether \(f\) is a one-to-one or a many-to-one function.
Markscheme
\(f'(x) = 3{x^2} + {{\text{e}}^x}\) A1
Note: Accept labelled diagram showing the graph \(y = f'(x)\) above the x-axis;
do not accept unlabelled graphs nor graph of \(y = f(x)\).
EITHER
this is always \( > 0\) R1
so the function is (strictly) increasing R1
and thus \(1 - 1\) A1
OR
this is always \( > 0\;\;\;{\text{(accept }} \ne 0{\text{)}}\) R1
so there are no turning points R1
and thus \(1 - 1\) A1
Note: A1 is dependent on the first R1.
[4 marks]
Examiners report
The differentiation was normally completed correctly, but then a large number did not realise what was required to determine the type of the original function. Most candidates scored 1/4 and wrote explanations that showed little or no understanding of the relation between first derivative and the given function. For example, it was common to see comments about horizontal and vertical line tests but applied to the incorrect function.In term of mathematical language, it was noted that candidates used many terms incorrectly showing no knowledge of the meaning of terms like ‘parabola’, ‘even’ or ‘odd’ ( or no idea about these concepts).
When carpet is manufactured, small faults occur at random. The number of faults in Premium carpets can be modelled by a Poisson distribution with mean 0.5 faults per 20\(\,\)m2. Mr Jones chooses Premium carpets to replace the carpets in his office building. The office building has 10 rooms, each with the area of 80\(\,\)m2.
Find the probability that the carpet laid in the first room has fewer than three faults.
Find the probability that exactly seven rooms will have fewer than three faults in the carpet.
Markscheme
\(\lambda = 4 \times 0.5\) (M1)
\(\lambda = 2\) (A1)
\({\text{P}}(X \leqslant 2) = 0.677\) A1
[3 marks]
\(Y \sim B(10,{\text{ }}0,677)\) (M1)(A1)
\({\text{P}}(Y = 7) = 0.263\) A1
Note: Award M1 for clear recognition of binomial distribution.
[3 marks]
Examiners report
Sketch the graph of \(y = {(x - 5)^2} - 2\left| {x - 5} \right| - 9,{\text{ for }}0 \le x \le 10\).
Hence, or otherwise, solve the equation \({(x - 5)^2} - 2\left| {x - 5} \right| - 9 = 0\).
Markscheme
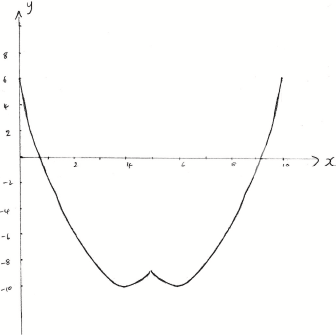
general shape including \[(\) minimums, cusp A1A1
correct domain and symmetrical about the middle \((x = 5)\) A1
[3 marks]
\(x = 9.16\;\;\;{\text{or}}\;\;\;x = 0.838\) A1A1
[2 marks]
Total [5 marks]
Examiners report
The probability density function of a continuous random variable \(X\) is given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}} {0,{\text{ }}x < 0} \\ {\frac{{\sin x}}{4},{\text{ }}0 \le x \le \pi } \\ {a(x - \pi ),{\text{ }}\pi < x \le 2\pi } \\ {0,{\text{ }}2\pi < x} \end{array}.} \right.\]
Sketch the graph \(y = f(x)\).
Find \({\text{P}}(X \le \pi )\).
Show that \(a = \frac{1}{{{\pi ^2}}}\).
Write down the median of \(X\).
Calculate the mean of \(X\).
Calculate the variance of \(X\).
Find \({\text{P}}\left( {\frac{\pi }{2} \le X \le \frac{{3\pi }}{2}} \right)\).
Given that \(\frac{\pi }{2} \le X \le \frac{{3\pi }}{2}\) find the probability that \(\pi \le X \le 2\pi \).
Markscheme
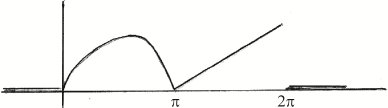
Award A1 for sine curve from \(0\) to \(\pi \), award A1 for straight line from \(\pi \) to \(2\pi \) A1A1
[2 marks]
\(\int_0^\pi {\frac{{\sin x}}{4}{\text{d}}x = \frac{1}{2}} \) (M1)A1
[2 marks]
METHOD 1
require \(\frac{1}{2} + \int_\pi ^{2\pi } {a(x - \pi ){\text{d}}x = 1} \) (M1)
\( \Rightarrow \frac{1}{2} + a\left[ {\frac{{{{(x - \pi )}^2}}}{2}} \right]_\pi ^{2\pi } = 1\;\;\;\left( {{\text{or }}\frac{1}{2} + a\left[ {\frac{{{x^2}}}{2} - \pi x} \right]_\pi ^{2\pi } = 1} \right)\) A1
\( \Rightarrow a\frac{{{\pi ^2}}}{2} = \frac{1}{2}\) A1
\( \Rightarrow a = \frac{1}{{{\pi ^2}}}\) AG
Note: Must obtain the exact value. Do not accept answers obtained with calculator.
METHOD 2
\(0.5 + {\text{ area of triangle }} = 1\) R1
area of triangle \( = \frac{1}{2}\pi \times a\pi = 0.5\) M1A1
Note: Award M1 for correct use of area formula \( = 0.5\), A1 for \(a\pi \).
\(a = \frac{1}{{{\pi ^2}}}\) AG
[3 marks]
median is \(\pi \) A1
[1 mark]
\(\mu = \int_0^\pi {x \cdot \frac{{\sin x}}{4}{\text{d}}x + \int_\pi ^{2\pi } {x \cdot \frac{{x - \pi }}{{{\pi ^2}}}{\text{d}}x} } \) (M1)(A1)
\( = 3.40339 \ldots = 3.40\;\;\;\left( {{\text{or }}\frac{\pi }{4} + \frac{{5\pi }}{6} = \frac{{13}}{{12}}\pi } \right)\) A1
[3 marks]
For \(\mu = 3.40339 \ldots \)
EITHER
\({\sigma ^2} = \int_0^\pi {{x^2} \cdot \frac{{\sin x}}{4}{\text{d}}x + \int_\pi ^{2\pi } {{x^2} \cdot \frac{{x - \pi }}{{{\pi ^2}}}{\text{d}}x - {\mu ^2}} } \) (M1)(A1)
OR
\({\sigma ^2} = \int_0^\pi {{{(x - \mu )}^2} \cdot \frac{{\sin x}}{4}{\text{d}}x + \int_\pi ^{2\pi } {{{(x - \mu )}^2} \cdot \frac{{x - \pi }}{{{\pi ^2}}}{\text{d}}x} } \) (M1)(A1)
THEN
\( = 3.866277 \ldots = 3.87\) A1
[3 marks]
\(\int_{\frac{\pi }{2}}^\pi {\frac{{\sin x}}{4}{\text{d}}x + \int_\pi ^{\frac{{3\pi }}{2}} {\frac{{x - \pi }}{{{\pi ^2}}}{\text{d}}x = 0.375\;\;\;\left( {{\text{or }}\frac{1}{4} + \frac{1}{8} = \frac{3}{8}} \right)} } \) (M1)A1
[2 marks]
\({\text{P}}\left( {\pi \le X \le 2\pi \left| {\frac{\pi }{2} \le X \le \frac{{3\pi }}{2}} \right.} \right) = \frac{{{\text{P}}\left( {\pi \le X \le \frac{{3\pi }}{2}} \right)}}{{{\text{P}}\left( {\frac{\pi }{2} \le X \le \frac{{3\pi }}{2}} \right)}}\) (M1)(A1)
\( = \frac{{\int_\pi ^{\frac{{3\pi }}{2}} {\frac{{(x - \pi )}}{{{\pi ^2}}}{\text{d}}x} }}{{0.375}} = \frac{{0.125}}{{0.375}}\;\;\;\left( {{\text{or }} = \frac{{\frac{1}{8}}}{{\frac{3}{8}}}{\text{ from diagram areas}}} \right)\) (M1)
\( = \frac{1}{3}\;\;\;(0.333)\) A1
[4 marks]
Total [20 marks]
Examiners report
Most candidates sketched the graph correctly. In a few cases candidates did not seem familiar with the shape of the graphs and ignored the fact that the graph represented a pdf. The correct sketch assisted greatly in the rest of the question.
Most candidates answered this question correctly.
A few good proofs were seen but also many poor answers where the candidates assumed what you were trying to prove and verified numerically the result.
Most candidates stated the value correctly but many others showed no understanding of the concept.
Many candidates scored full marks in this question; many others could not apply the formula due to difficulties in dealing with the piecewise function. For example, a number of candidates divided the final answer by two.
Many misconceptions were identified: use of incorrect formula (e.g. formula for discrete distributions), use of both expressions as integrand and division of the result by 2 at the end.
This part was fairly well done with many candidates achieving full marks.
Many candidates had difficulties with this part showing that the concept of conditional probability was poorly understood. The best candidates did it correctly from the sketch.
The vertical cross-section of a container is shown in the following diagram.
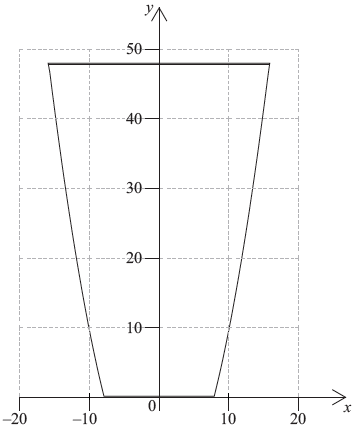
The curved sides of the cross-section are given by the equation \(y = 0.25{x^2} - 16\). The horizontal cross-sections are circular. The depth of the container is \(48\) cm.
If the container is filled with water to a depth of \(h\,{\text{cm}}\), show that the volume, \(V\,{\text{c}}{{\text{m}}^3}\), of the water is given by \(V = 4\pi \left( {\frac{{{h^2}}}{2} + 16h} \right)\).
The container, initially full of water, begins leaking from a small hole at a rate given by \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = - \frac{{250\sqrt h }}{{\pi(h + 16)}}\) where \(t\) is measured in seconds.
(i) Show that \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = - \frac{{250\sqrt h }}{{4{\pi ^2}{{(h + 16)}^2}}}\).
(ii) State \(\frac{{{\text{d}}t}}{{{\text{d}}h}}\) and hence show that \(t = \frac{{ - 4{\pi ^2}}}{{250}}\int {\left( {{h^{\frac{3}{2}}} + 32{h^{\frac{1}{2}}} + 256{h^{ - \frac{1}{2}}}} \right){\text{d}}h} \).
(iii) Find, correct to the nearest minute, the time taken for the container to become empty. (\(60\) seconds = 1 minute)
Once empty, water is pumped back into the container at a rate of \(8.5\;{\text{c}}{{\text{m}}^3}{{\text{s}}^{ - 1}}\). At the same time, water continues leaking from the container at a rate of \(\frac{{250\sqrt h }}{{\pi (h + 16)}}{\text{c}}{{\text{m}}^3}{{\text{s}}^{ - 1}}\).
Using an appropriate sketch graph, determine the depth at which the water ultimately stabilizes in the container.
Markscheme
attempting to use \(V = \pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
attempting to express \({x^2}\) in terms of \(y\) ie \({x^2} = 4(y + 16)\) (M1)
for \(y = h,{\text{ }}V = 4\pi \int_0^h {y + 16{\text{d}}y} \) A1
\(V = 4\pi \left( {\frac{{{h^2}}}{2} + 16h} \right)\) AG
[3 marks]
(i) METHOD 1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}h}}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}\) (M1)
\(\frac{{{\text{d}}V}}{{{\text{d}}h}} = 4\pi (h + 16)\) (A1)
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{4\pi (h + 16)}} \times \frac{{ - 250\sqrt h }}{{\pi (h + 16)}}\) M1A1
Note: Award M1 for substitution into \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{{\text{d}}h}}{{{\text{d}}V}} \times \frac{{{\text{d}}V}}{{{\text{d}}t}}\).
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{250\sqrt h }}{{4{\pi ^2}{{(h + 16)}^2}}}\) AG
METHOD 2
\(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 4\pi (h + 16)\frac{{{\text{d}}h}}{{{\text{d}}t}}\;\;\;\)(implicit differentiation)(M1)
\(\frac{{ - 250\sqrt h }}{{\pi (h + 16)}} = 4\pi (h + 16)\frac{{{\text{d}}h}}{{{\text{d}}t}}\;\;\;\)(or equivalent) A1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{1}{{4\pi (h + 16)}} \times \frac{{ - 250\sqrt h }}{{\pi (h + 16)}}\) M1A1
\(\frac{{{\text{d}}h}}{{{\text{d}}t}} = \frac{{250\sqrt h }}{{4{\pi ^2}{{(h + 16)}^2}}}\) AG
(ii) \(\frac{{{\text{d}}t}}{{{\text{d}}h}} = - \frac{{4{\pi ^2}{{(h + 16)}^2}}}{{250\sqrt h }}\) A1
\(t = \int { - \frac{{4{\pi ^2}{{(h + 16)}^2}}}{{250\sqrt h }}} {\text{d}}h\) (M1)
\(t = \int { - \frac{{4{\pi ^2}({h^2} + 32h + 256)}}{{250\sqrt h }}} {\text{d}}h\) A1
\(t = \frac{{ - 4{\pi ^2}}}{{250}}\int {\left( {{h^{\frac{3}{2}}} + 32{h^{\frac{1}{2}}} + 256{h^{ - \frac{1}{{2}}}}} \right){\text{d}}h} \) AG
(iii) METHOD 1
\(t = \frac{{ - 4{\pi ^2}}}{{250}}\int_{48}^0 {\left( {{h^{\frac{3}{2}}} + 32{h^{\frac{1}{2}}} + 256{h^{ - \frac{1}{2}}}} \right)} {\text{d}}h\) (M1)
\(t = 2688.756 \ldots {\text{ (s)}}\) (A1)
\(45\) minutes (correct to the nearest minute) A1
METHOD 2
\(t = \frac{{ - 4{\pi ^2}}}{{250}}\left( {\frac{2}{5}{h^{\frac{5}{2}}} + \frac{{64}}{3}{h^{\frac{3}{2}}} + 512{h^{\frac{1}{2}}}} \right) + c\)
when \(t = 0,{\text{ }}h = 48 \Rightarrow c = 2688.756 \ldots \left( {c = \frac{{4{\pi ^2}}}{{250}}\left( {\frac{2}{5} \times {{48}^{\frac{5}{2}}} + \frac{{64}}{3} \times {{48}^{\frac{3}{2}}} + 512 \times {{48}^{\frac{1}{2}}}} \right)} \right)\) (M1)
when \(h = 0,{\text{ }}t = 2688.756 \ldots \left( {t = \frac{{4{\pi ^2}}}{{250}}\left( {\frac{2}{5} \times {{48}^{\frac{5}{2}}} + \frac{{64}}{3} \times {{48}^{\frac{3}{2}}} + 512 \times {{48}^{\frac{1}{2}}}} \right)} \right){\text{ (s)}}\) (A1)
45 minutes (correct to the nearest minute) A1
[10 marks]
EITHER
the depth stabilizes when \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 0\;\;\;ie\;\;\;8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}} = 0\) R1
attempting to solve \(8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}} = 0\;\;\;{\text{for }}h\) (M1)
OR
the depth stabilizes when \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = 0\;\;\;ie\;\;\;\frac{1}{{4\pi (h + 16)}}\left( {8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}}} \right) = 0\) R1
attempting to solve \(\frac{1}{{4\pi (h + 16)}}\left( {8.5 - \frac{{250\sqrt h }}{{\pi (h + 16)}}} \right) = 0\;\;\;{\text{for }}h\) (M1)
THEN
\(h = 5.06{\text{ (cm)}}\) A1
[3 marks]
Total [16 marks]
Examiners report
This question was done reasonably well by a large proportion of candidates. Many candidates however were unable to show the required result in part (a). A number of candidates seemingly did not realize how the container was formed while other candidates attempted to fudge the result.
Part (b) was quite well done. In part (b) (i), most candidates were able to correctly calculate \(\frac{{{\text{d}}V}}{{{\text{d}}h}}\) and correctly apply a related rates expression to show the given result. Some candidates however made a sign error when stating \(\frac{{{\text{d}}V}}{{{\text{d}}t}}\). A large number of candidates successfully answered part (b) (ii). In part (b) (iii), successful candidates either set up and calculated an appropriate definite integral or antidifferentiated and found that \(t = C\) when \(h = 0\).
In part (c), a pleasing number of candidates realized that the water depth stabilized when either \(\frac{{{\text{d}}V}}{{{\text{d}}t}} = 0\) or \(\frac{{{\text{d}}h}}{{{\text{d}}t}} = 0\), sketched an appropriate graph and found the correct value of \(h\). Some candidates misinterpreted the situation and attempted to find the coordinates of the local minimum of their graph.
The seventh, third and first terms of an arithmetic sequence form the first three terms of a geometric sequence.
The arithmetic sequence has first term \(a\) and non-zero common difference \(d\).
Show that \(d = \frac{a}{2}\).
The seventh term of the arithmetic sequence is \(3\). The sum of the first \(n\) terms in the arithmetic sequence exceeds the sum of the first \(n\) terms in the geometric sequence by at least \(200\).
Find the least value of \(n\) for which this occurs.
Markscheme
using \(r = \frac{{{u_2}}}{{{u_1}}} = \frac{{{u_3}}}{{{u_2}}}\) to form \(\frac{{a + 2d}}{{a + 6d}} = \frac{a}{{a + 2d}}\) (M1)
\(a(a + 6d) = {(a + 2d)^2}\) A1
\(2d(2d - a) = 0\;\;\;\)(or equivalent) A1
since \(d \ne 0 \Rightarrow d = \frac{a}{2}\) AG
[3 marks]
substituting \(d = \frac{a}{2}\) into \(a + 6d = 3\) and solving for \(a\) and \(d\) (M1)
\(a = \frac{3}{4}\) and \(d = \frac{3}{8}\) (A1)
\(r = \frac{1}{2}\) A1
\(\frac{n}{2}\left( {2 \times \frac{3}{4} + (n - 1)\frac{3}{8}} \right) - \frac{{3\left( {1 - {{\left( {\frac{1}{2}} \right)}^n}} \right)}}{{1 - \frac{1}{2}}} \ge 200\) (A1)
attempting to solve for \(n\) (M1)
\(n \ge 31.68 \ldots \)
so the least value of \(n\) is 32 A1
[6 marks]
Total [9 marks]
Examiners report
Part (a) was reasonably well done. A number of candidates used \(r = \frac{{{u_1}}}{{{u_2}}} = \frac{{{u_2}}}{{{u_3}}}\) rather than \(r = \frac{{{u_2}}}{{{u_1}}} = \frac{{{u_3}}}{{{u_2}}}\). This invariably led to candidates obtaining \(r = 2\) in part (b).
In part (b), most candidates were able to correctly find the first term and the common difference for the arithmetic sequence. However a number of candidates either obtained \(r = 2\) via means described in part (a) or confused the two sequences and used \({u_1} = \frac{3}{4}\) for the geometric sequence.
Let \(z = r(\cos \alpha + {\text{i}}\sin \alpha )\), where \(\alpha \) is measured in degrees, be the solution of \({z^5} - 1 = 0\) which has the smallest positive argument.
(i) Use the binomial theorem to expand \({(\cos \theta + {\text{i}}\sin \theta )^5}\).
(ii) Hence use De Moivre’s theorem to prove
\[\sin 5\theta = 5{\cos ^4}\theta \sin \theta - 10{\cos ^2}\theta {\sin ^3}\theta + {\sin ^5}\theta .\]
(iii) State a similar expression for \(\cos 5\theta \) in terms of \(\cos \theta \) and \(\sin \theta \).
Find the value of \(r\) and the value of \(\alpha \).
Using (a) (ii) and your answer from (b) show that \(16{\sin ^4}\alpha - 20{\sin ^2}\alpha + 5 = 0\).
Hence express \(\sin 72^\circ \) in the form \(\frac{{\sqrt {a + b\sqrt c } }}{d}\) where \(a,{\text{ }}b,{\text{ }}c,{\text{ }}d \in \mathbb{Z}\).
Markscheme
(i) \({(\cos \theta + {\text{i}}\sin \theta )^5}\)
\( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta + 10{{\text{i}}^2}{\cos ^3}\theta {\sin ^2}\theta + \)
\(10{{\text{i}}^3}{\cos ^2}\theta {\sin ^3}\theta + 5{{\text{i}}^4}\cos \theta {\sin ^4}\theta + {{\text{i}}^5}{\sin ^5}\theta \) A1A1
\(( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta - 10{\cos ^3}\theta {\sin ^2}\theta - \)
\(10{\text{i}}{\cos ^2}\theta {\sin ^3}\theta + 5\cos \theta {\sin ^4}\theta + {\text{i}}{\sin ^5}\theta )\)
Note: Award first A1 for correct binomial coefficients.
(ii) \({({\text{cis}}\theta )^5} = {\text{cis}}5\theta = \cos 5\theta + {\text{i}}\sin 5\theta \) M1
\( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta - 10{\cos ^3}\theta {\sin ^2}\theta - 10{\text{i}}{\cos ^2}\theta {\sin ^3}\theta + \)
\(5\cos \theta {\sin ^4}\theta + {\text{i}}{\sin ^5}\theta \) A1
Note: Previous line may be seen in (i)
equating imaginary terms M1
\(\sin 5\theta = 5{\cos ^4}\theta \sin \theta - 10{\cos ^2}\theta {\sin ^3}\theta + {\sin ^5}\theta \) AG
(iii) equating real terms
\(\cos 5\theta = {\cos ^5}\theta - 10{\cos ^3}\theta {\sin ^2}\theta + 5\cos \theta {\sin ^4}\theta \) A1
[6 marks]
\({(r{\text{cis}}\alpha )^5} = 1 \Rightarrow {r^5}{\text{cis}}5\alpha = 1{\text{cis}}0\) M1
\({r^5} = 1 \Rightarrow r = 1\) A1
\(5\alpha = 0 \pm 360k,{\text{ }}k \in \mathbb{Z} \Rightarrow a = 72k\) (M1)
\(\alpha = 72^\circ \) A1
Note: Award M1A0 if final answer is given in radians.
[4 marks]
use of \(\sin (5 \times 72) = 0\) OR the imaginary part of \(1\) is \(0\) (M1)
\(0 = 5{\cos ^4}\alpha \sin \alpha - 10{\cos ^2}\alpha {\sin ^3}\alpha + {\sin ^5}\alpha \) A1
\(\sin \alpha \ne 0 \Rightarrow 0 = 5{(1 - {\sin ^2}\alpha )^2} - 10(1 - {\sin ^2}\alpha ){\sin ^2}\alpha + {\sin ^4}\alpha \) M1
Note: Award M1 for replacing \({\cos ^2}\alpha \).
\(0 = 5(1 - 2{\sin ^2}\alpha + {\sin ^4}\alpha ) - 10{\sin ^2}\alpha + 10{\sin ^4}\alpha + {\sin ^4}\alpha \) A1
Note: Award A1 for any correct simplification.
so \(16{\sin ^4}\alpha - 20{\sin ^2}\alpha + 5 = 0\) AG
[4 marks]
\({\sin ^2}\alpha = \frac{{20 \pm \sqrt {400 - 320} }}{{32}}\) M1A1
\(\sin \alpha = \pm \sqrt {\frac{{20 \pm \sqrt {80} }}{{32}}} \)
\(\sin \alpha = \frac{{ \pm \sqrt {10 \pm 2\sqrt 5 } }}{4}\) A1
Note: Award A1 regardless of signs. Accept equivalent forms with integral denominator, simplification may be seen later.
as \(72 > 60\), \(\sin 72 > \frac{{\sqrt 3 }}{2} = 0.866 \ldots \) we have to take both positive signs (or equivalent argument) R1
Note: Allow verification of correct signs with calculator if clearly stated
\(\sin 72 = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4}\) A1
[5 marks]
Total [19 marks]
Examiners report
In part (i) many candidates tried to multiply it out the binomials rather than using the binomial theorem. In parts (ii) and (iii) many candidates showed poor understanding of complex numbers and made no attempt to equate real and imaginary parts. In a some cases the correct answer to part (iii) was seen although it was unclear how it was obtained.
This question was poorly done. Very few candidates made a good attempt to apply De Moivre’s theorem and most of them could not even equate the moduli to obtain \(r\).
This question was poorly done. From the few candidates that attempted it, many candidates started by writing down what they were trying to prove and made no progress.
Very few made a serious attempt to answer this question. Also very few realised that they could use the answers given in part (c) to attempt this part.
Consider \(f(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right)\)
The function \(f\) is defined by \(f(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right),{\text{ }}x \in D\)
The function \(g\) is defined by \(g(x) = - 1 + \ln \left( {\sqrt {{x^2} - 1} } \right),{\text{ }}x \in \left] {1,{\text{ }}\infty } \right[\).
Find the largest possible domain \(D\) for \(f\) to be a function.
Sketch the graph of \(y = f(x)\) showing clearly the equations of asymptotes and the coordinates of any intercepts with the axes.
Explain why \(f\) is an even function.
Explain why the inverse function \({f^{ - 1}}\) does not exist.
Find the inverse function \({g^{ - 1}}\) and state its domain.
Find \(g'(x)\).
Hence, show that there are no solutions to \(g'(x) = 0\);
Hence, show that there are no solutions to \(({g^{ - 1}})'(x) = 0\).
Markscheme
\({x^2} - 1 > 0\) (M1)
\(x < - 1\) or \(x > 1\) A1
[2 marks]
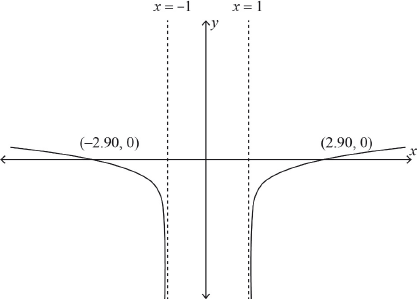
shape A1
\(x = 1\) and \(x = - 1\) A1
\(x\)-intercepts A1
[3 marks]
EITHER
\(f\) is symmetrical about the \(y\)-axis R1
OR
\(f( - x) = f(x)\) R1
[1 mark]
EITHER
\(f\) is not one-to-one function R1
OR
horizontal line cuts twice R1
Note: Accept any equivalent correct statement.
[1 mark]
\(x = - 1 + \ln \left( {\sqrt {{y^2} - 1} } \right)\) M1
\({{\text{e}}^{2x + 2}} = {y^2} - 1\) M1
\({g^{ - 1}}(x) = \sqrt {{{\text{e}}^{2x + 2}} + 1} ,{\text{ }}x \in \mathbb{R}\) A1A1
[4 marks]
\(g'(x) = \frac{1}{{\sqrt {{x^2} - 1} }} \times \frac{{2x}}{{2\sqrt {{x^2} - 1} }}\) M1A1
\(g'(x) = \frac{x}{{{x^2} - 1}}\) A1
[3 marks]
\(g'(x) = \frac{x}{{{x^2} - 1}} = 0 \Rightarrow x = 0\) M1
which is not in the domain of \(g\) (hence no solutions to \(g'(x) = 0\)) R1
[2 marks]
\(({g^{ - 1}})'(x) = \frac{{{{\text{e}}^{2x + 2}}}}{{\sqrt {{{\text{e}}^{2x + 2}} + 1} }}\) M1
as \({{\text{e}}^{2x + 2}} > 0 \Rightarrow ({g^{ - 1}})'(x) > 0\) so no solutions to \(({g^{ - 1}})'(x) = 0\) R1
Note: Accept: equation \({{\text{e}}^{2x + 2}} = 0\) has no solutions.
[2 marks]
Examiners report
Let \(f(x) = {x^4} + 0.2{x^3} - 5.8{x^2} - x + 4,{\text{ }}x \in \mathbb{R}\).
The domain of \(f\) is now restricted to \([0,{\text{ }}a]\).
Let \(g(x) = 2\sin (x - 1) - 3,{\text{ }} - \frac{\pi }{2} + 1 \leqslant x \leqslant \frac{\pi }{2} + 1\).
Find the solutions of \(f(x) > 0\).
For the curve \(y = f(x)\).
(i) Find the coordinates of both local minimum points.
(ii) Find the \(x\)-coordinates of the points of inflexion.
Write down the largest value of \(a\) for which \(f\) has an inverse. Give your answer correct to 3 significant figures.
For this value of a sketch the graphs of \(y = f(x)\) and \(y = {f^{ - 1}}(x)\) on the same set of axes, showing clearly the coordinates of the end points of each curve.
Solve \({f^{ - 1}}(x) = 1\).
Find an expression for \({g^{ - 1}}(x)\), stating the domain.
Solve \(({f^{ - 1}} \circ g)(x) < 1\).
Markscheme
valid method eg, sketch of curve or critical values found (M1)
\(x < - 2.24,{\text{ }}x > 2.24,\) A1
\( - 1 < x < 0.8\) A1
Note: Award M1A1A0 for correct intervals but with inclusive inequalities.
[3 marks]
(i) \((1.67,{\text{ }} - 5.14),{\text{ }}( - 1.74,{\text{ }} - 3.71)\) A1A1
Note: Award A1A0 for any two correct terms.
(ii) \(f'(x) = 4{x^3} + 0.6{x^2} - 11.6x - 1\)
\(f''(x) = 12{x^2} + 1.2x - 11.6 = 0\) (M1)
\( - 1.03,{\text{ }}0.934\) A1A1
Note: M1 should be awarded if graphical method to find zeros of \(f''(x)\) or turning points of \(f'(x)\) is shown.
[5 marks]
1.67 A1
[2 marks]
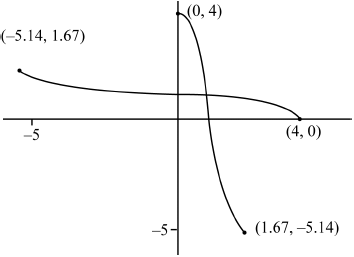 M1A1A1
M1A1A1
Note: Award M1 for reflection of their \(y = f(x)\) in the line \(y = x\) provided their \(f\) is one-one.
A1 for \((0,{\text{ }}4)\), \((4,{\text{ }}0)\) (Accept axis intercept values) A1 for the other two sets of coordinates of other end points
[2 marks]
\(x = f(1)\) M1
\( = - 1.6\) A1
[2 marks]
\(y = 2\sin (x - 1) - 3\)
\(x = 2\sin (y - 1) - 3\) (M1)
\(\left( {{g^{ - 1}}(x) = } \right){\text{ }}\arcsin \left( {\frac{{x + 3}}{2}} \right) + 1\) A1
\( - 5 \leqslant x \leqslant - 1\) A1A1
Note: Award A1 for −5 and −1, and A1 for correct inequalities if numbers are reasonable.
[8 marks]
\({f^{ - 1}}\left( {g(x)} \right) < 1\)
\(g(x) > - 1.6\) (M1)
\(x > {g^{ - 1}}( - 1.6) = 1.78\) (A1)
Note: Accept = in the above.
\(1.78 < x \leqslant \frac{\pi }{2} + 1\) A1A1
Note: A1 for \(x > 1.78\) (allow ≥) and A1 for \(x \leqslant \frac{\pi }{2} + 1\).
[4 marks]
Examiners report
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Parts (a) and (b) were well answered, with considerably less success in part (c). Surprisingly few students were able to reflect the curve in \(y = x\) satisfactorily, and many were not making their sketch using the correct domain.
Part d(i) was generally well done, but there were few correct answers for d(ii).
Part d(i) was generally well done, but there were few correct answers for d(ii).
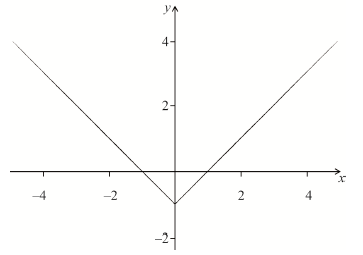
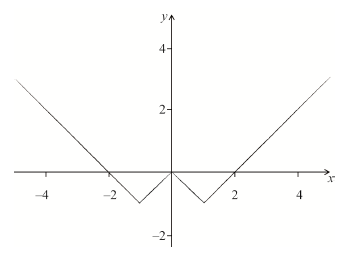
Let \(f(x) = \left| x \right| - 1\).
(a) The graph of \(y = g(x)\) is drawn below.

(i) Find the value of \((f \circ g)(1)\).
(ii) Find the value of \((f \circ g \circ g)(1)\).
(iii) Sketch the graph of \(y = (f \circ g)(x)\).
(b) (i) Sketch the graph of \(y = f(x)\).
(ii) State the zeros of f.
(c) (i) Sketch the graph of \(y = (f \circ f)(x)\).
(ii) State the zeros of \(f \circ f\).
(d) Given that we can denote \(\underbrace {f \circ f \circ f \circ \ldots \circ f}_{n{\text{ times}}}\) as \({f^n}\),
(i) find the zeros of \({f^3}\);
(ii) find the zeros of \({f^4}\);
(iii) deduce the zeros of \({f^8}\).
(e) The zeros of \({f^{2n}}\) are \({a_1},{\text{ }}{a_2},{\text{ }}{a_3},{\text{ }} \ldots {\text{, }}{a_N}\).
(i) State the relation between n and N;
(ii) Find, and simplify, an expression for \(\sum\limits_{r = 1}^N {\left| {{a_r}} \right|} \) in terms of n.
Markscheme
(a) (i) \(f(0) = - 1\) (M1)A1
(ii) \((f \circ g)(0) = f(4) = 3\) A1
(iii)
 (M1)A1
(M1)A1
Note: Award M1 for evidence that the lower part of the graph has been reflected and A1 correct shape with y-intercept below 4.
[5 marks]
(b) (i)
 (M1)A1
(M1)A1
Note: Award M1 for any translation of \(y = \left| x \right|\).
(ii) \( \pm 1\) A1
Note: Do not award the A1 if coordinates given, but do not penalise in the rest of the question
[3 marks]
(c) (i)
 (M1)A1
(M1)A1
Note: Award M1 for evidence that lower part of (b) has been reflected in the x-axis and translated.
(ii) \(0,{\text{ }} \pm 2\) A1
[3 marks]
(d) (i) \( \pm 1,{\text{ }} \pm 3\) A1
(ii) \(0,{\text{ }} \pm 2,{\text{ }} \pm 4\) A1
(iii) \(0,{\text{ }} \pm 2,{\text{ }} \pm 4,{\text{ }} \pm 6,{\text{ }} \pm 8\) A1
[3 marks]
(e) (i) \({\text{(1, 3), (2, 5), }} \ldots \) (M1)
\(N = 2n + 1\) A1
(ii) Using the formula of the sum of an arithmetic series (M1)
EITHER
\(4(1 + 2 + 3 + \ldots + n) = \frac{4}{2}n(n + 1)\)
\( = 2n(n + 1)\) A1
OR
\(2(2 + 4 + 6 + \ldots + 2n) = \frac{2}{2}n(2n + 2)\)
\( = 2n(n + 1)\) A1
[4 marks]
Total [18 marks]
Examiners report
The function \(f\) is given by \(f(x) = \frac{{3{x^2} + 10}}{{{x^{\text{2}}} - 4}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 2,{\text{ }}x \ne - 2\).
Prove that \(f\) is an even function.
Sketch the graph \(y = f(x)\).
Write down the range of \(f\).
Markscheme
\(f( - x) = \frac{{3{{( - x)}^2} + 10}}{{{{( - x)}^2} - 4}}\) A1
\( = \frac{{3{x^2} + 10}}{{{x^2} - 4}} = f(x)\)
\(f(x) = f( - x)\) R1
hence this is an even function AG
Note: Award A1R1 for the statement, all the powers are even hence \(f(x) = f( - x)\).
Note: Just stating all the powers are even is A0R0.
Note: Do not accept arguments based on the symmetry of the graph.
[2 marks]
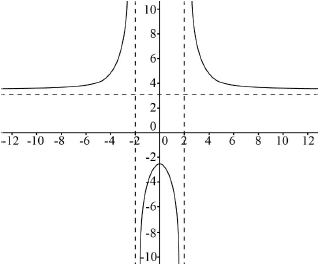
correct shape in 3 parts which are asymptotic and symmetrical A1
correct vertical asymptotes clear at 2 and –2 A1
correct horizontal asymptote clear at 3 A1
[3 marks]
\(f(x) > 3\) A1
\(f(x) \leqslant - 2.5\) A1
[2 marks]
Examiners report
Most candidates were able to prove that a function was even, although many attempted to show special cases, rather than a general proof. Many lost marks through not showing the asymptotes on their sketch. Marks were commonly lost in incorrect use of inequalities for the range of the function.
Most candidates were able to prove that a function was even, although many attempted to show special cases, rather than a general proof. Many lost marks through not showing the asymptotes on their sketch. Marks were commonly lost in incorrect use of inequalities for the range of the function.
Most candidates were able to prove that a function was even, although many attempted to show special cases, rather than a general proof. Many lost marks through not showing the asymptotes on their sketch. Marks were commonly lost in incorrect use of inequalities for the range of the function.
Find the set of values of x for which \(\left| {0.1{x^2} - 2x + 3} \right| < {\log _{10}}x\) .
Markscheme
Attempting to solve \(\left| {0.1{x^2} - 2x + 3} \right| = {\log _{10}}x\) numerically or graphically. (M1)
x = 1.52, 1.79 (A1)(A1)
x = 17.6, 19.1 (A1)
\((1.52 < x < 1.79) \cup (17.6 < x < 19.1)\) A1A1 N2
[6 marks]
Examiners report
This question was generally not well done. A number of candidates attempted an ‘ill-fated’ algebraic approach. Most candidates who used their GDC were able to correctly locate one inequality. The few successful candidates were able to employ a suitable window or suitable window(s) to correctly locate both inequalities.
Consider the functions \(f(x) = {x^3} + 1\) and \(g(x) = \frac{1}{{{x^3} + 1}}\). The graphs of \(y = f(x)\) and \(y = g(x)\) meet at the point (0, 1) and one other point, P.
Find the coordinates of P.
Calculate the size of the acute angle between the tangents to the two graphs at the point P.
Markscheme
\({x^3} + 1 = \frac{1}{{{x^3} + 1}}\)
\(( - 1.26, - 1)\,\,\,\,\,\left( { = \left( { - \sqrt[3]{2}, - 1} \right)} \right)\) A1
[1 mark]
\(f'( - 1.259...) = 4.762…\) \((3 \times {2^{\frac{2}{3}}})\) A1
\(g'( - 1.259...) = - 4.762…\) \(( - 3 \times {2^{\frac{2}{3}}})\) A1
required angle \( = 2\arctan \left( {\frac{1}{{4.762...}}} \right)\) M1
\( = 0.414\) (accept 23.7 ) A1
Note: Accept alternative methods including finding the obtuse angle first.
[4 marks]
Examiners report
In part (a) almost all candidates obtained the correct answer, either in numerical form or in exact form. Although many candidates scored one mark in (b), for one gradient, few scored any more. Successful candidates almost always adopted a vector approach to finding the angle between the two tangents, rather than using trigonometry.
In part (a) almost all candidates obtained the correct answer, either in numerical form or in exact form. Although many candidates scored one mark in (b), for one gradient, few scored any more. Successful candidates almost always adopted a vector approach to finding the angle between the two tangents, rather than using trigonometry.
(a) Simplify the difference of binomial coefficients
\[\left( {\begin{array}{*{20}{c}}
n \\
3
\end{array}} \right) - \left( {\begin{array}{*{20}{c}}
{2n} \\
2
\end{array}} \right),{\text{ where }}n \geqslant 3.\]
(b) Hence, solve the inequality
\[\left( {\begin{array}{*{20}{c}}
n \\
3
\end{array}} \right) - \left( {\begin{array}{*{20}{c}}
{2n} \\
2
\end{array}} \right) > 32n,{\text{ where }}n \geqslant 3.\]
Markscheme
(a) the expression is
\(\frac{{n!}}{{(n - 3)!3!}} - \frac{{(2n)!}}{{(2n - 2)!2!}}\) (A1)
\(\frac{{n(n - 1)(n - 2)}}{6} - \frac{{2n(2n - 1)}}{2}\) M1A1
\( = \frac{{n({n^2} - 15n + 8)}}{6}{\text{ }}\left( { = \frac{{{n^3} - 15{n^2} + 8n}}{6}} \right)\) A1
(b) the inequality is
\(\frac{{{n^3} - 15{n^2} + 8n}}{6} > 32n\)
attempt to solve cubic inequality or equation (M1)
\({n^3} - 15{n^2} - 184n > 0\,\,\,\,\,n(n - 23)(n + 8) > 0\)
\(n > 23\,\,\,\,\,(n \geqslant 24)\) A1
[6 marks]
Examiners report
Part(a) - Although most understood the notation, few knew how to simplify the binomial coefficients.
Part(b) - Many were able to solve the cubic, but some failed to report their answer as an integer inequality.
The function \(f(x) = 4{x^3} + 2ax - 7a\) , \(a \in \mathbb{R}\), leaves a remainder of \(−10\) when divided by \(\left( {x - a} \right)\) .
Find the value of \(a\) .
Show that for this value of \(a\) there is a unique real solution to the equation \(f (x) = 0\) .
Markscheme
\(f(a) = 4{a^3} + 2{a^2} - 7a = - 10\) M1
\(4{a^3} + 2{a^2} - 7a + 10 = 0\)
\(\left( {a + 2} \right)\left( {4{a^2} - 6a + 5} \right) = 0\) or sketch or GDC (M1)
\(a = - 2\) A1
[3 marks]
substituting \(a = - 2\) into \(f (x)\)
\(f(x) = 4{x^3} - 4x + 14 = 0\) A1
EITHER
graph showing unique solution which is indicated (must include max and min) R1
OR
convincing argument that only one of the solutions is real R1
(−1.74, 0.868 ±1.12i)
[5 marks]
Examiners report
Candidates found this question surprisingly challenging. The most straightforward approach was use of the Remainder Theorem but a significant number of candidates seemed unaware of this technique. This lack of knowledge led many candidates to attempt an algebraically laborious use of long division. In (b) a number of candidates did not seem to appreciate the significance of the word unique and hence found it difficult to provide sufficient detail to make a meaningful argument. However, most candidates did recognize that they needed a technological approach when attempting (b).
Candidates found this question surprisingly challenging. The most straightforward approach was use of the Remainder Theorem but a significant number of candidates seemed unaware of this technique. This lack of knowledge led many candidates to attempt an algebraically laborious use of long division. In (b) a number of candidates did not seem to appreciate the significance of the word unique and hence found it difficult to provide sufficient detail to make a meaningful argument. However, most candidates did recognize that they needed a technological approach when attempting (b).
Write down the quadratic expression \(2{x^2} + x - 3\) as the product of two linear factors.
Hence, or otherwise, find the coefficient of \(x\) in the expansion of \({\left( {2{x^2} + x - 3} \right)^8}\) .
Markscheme
\(2{x^2} + x - 3 = \left( {2x + 3} \right)\left( {x - 1} \right)\) A1
Note: Accept \(2\left( {x + \frac{3}{2}} \right)\left( {x - 1} \right)\).
Note: Either of these may be seen in (b) and if so A1 should be awarded.
[1 mark]
EITHER
\({\left( {2{x^2} + x - 3} \right)^8} = {\left( {2x + 3} \right)^8}{\left( {x - 1} \right)^8}\) M1
\( = \left( {{3^8} + 8\left( {{3^7}} \right)\left( {2x} \right) + ...} \right)\left( {{{\left( { - 1} \right)}^8} + 8{{\left( { - 1} \right)}^7}\left( x \right) + ...} \right)\) (A1)
coefficient of \(x = {3^8} \times 8 \times {\left( { - 1} \right)^7} + {3^7} \times 8 \times 2 \times {\left( { - 1} \right)^8}\) M1
= −17 496 A1
Note: Under ft, final A1 can only be achieved for an integer answer.
OR
\({\left( {2{x^2} + x - 3} \right)^8} = {\left( {3 - \left( {x - 2{x^2}} \right)} \right)^8}\) M1
\( = {3^8} + 8\left( { - \left( {x - 2{x^2}} \right)\left( {{3^7}} \right) + ...} \right)\) (A1)
coefficient of \(x = 8 \times \left( { - 1} \right) \times {3^7}\) M1
= −17 496 A1
Note: Under ft, final A1 can only be achieved for an integer answer.
[4 marks]
Examiners report
Many candidates struggled to find an efficient approach to this problem by applying the Binomial Theorem. A disappointing number of candidates attempted the whole expansion which was clearly an unrealistic approach when it is noted that the expansion is to the 8th power. The fact that some candidates wrote down Pascal’s Triangle suggested that they had not studied the Binomial Theorem in enough depth or in a sufficient variety of contexts.
Many candidates struggled to find an efficient approach to this problem by applying the Binomial Theorem. A disappointing number of candidates attempted the whole expansion which was clearly an unrealistic approach when it is noted that the expansion is to the 8th power. The fact that some candidates wrote down Pascal’s Triangle suggested that they had not studied the Binomial Theorem in enough depth or in a sufficient variety of contexts.
Consider \(f(x) = \ln x - {{\text{e}}^{\cos x}},{\text{ }}0 < x \leqslant 10\).
Sketch the graph of \(y = f(x)\), stating the coordinates of any maximum and minimum points and points of intersection with the x-axis.
Solve the inequality \(\ln x \leqslant {{\text{e}}^{\cos x}},{\text{ }}0 < x \leqslant 10\).
Markscheme
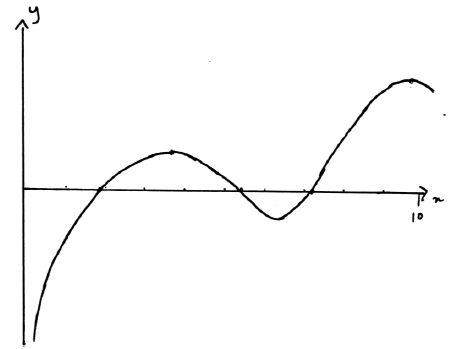
A correct graph shape for \(0 < x \leqslant 10\) A1
maxima (3.78, 0.882) and (9.70, 1.89) A1
minimum (6.22, –0.885) A1
x-axis intercepts (1.97, 0), (5.24, 0) and (7.11, 0) A2
Note: Award A1 if two x-axis intercepts are correct.
[5 marks]
\(0 < x \leqslant 1.97\) A1
\(5.24 \leqslant x \leqslant 7.11\) A1
[2 marks]
Examiners report
Part (a) was reasonably well done although more care was required when showing correct endpoint behaviour. A number of sketch graphs suggested the existence of either a vertical axis intercept or displayed an open circle on the vertical axis. A large number of candidates did not state the coordinates of the various key features correct to three significant figures. A large number of candidates did not locate the maximum near \(x = 10\). Most candidates were able to locate the x-axis intercepts and the minimum. A few candidates unfortunately sketched a graph from a GDC set in degrees.
In part (b), a number of candidates identified the correct critical values but used incorrect inequality signs. Some candidates attempted to solve the inequality algebraically.
The function f is defined as \(f(x) = - 3 + \frac{1}{{x - 2}},{\text{ }}x \ne 2\).
(i) Sketch the graph of \(y = f(x)\), clearly indicating any asymptotes and axes intercepts.
(ii) Write down the equations of any asymptotes and the coordinates of any axes intercepts.
Find the inverse function \({f^{ - 1}}\), stating its domain.
Markscheme
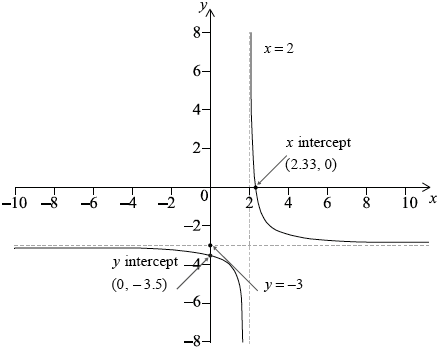 A1A1A1
A1A1A1
Note: Award A1 for correct shape, A1 for \(x = 2\) clearly stated and A1 for \(y = - 3\) clearly stated.
x intercept (2.33, 0) and y intercept (0, –3.5) A1
Note: Accept –3.5 and 2.33 (7/3) marked on the correct axes.
[4 marks]
\(x = - 3 + \frac{1}{{y - 2}}\) M1
Note: Award M1 for interchanging x and y (can be done at a later stage).
\(x + 3 = \frac{1}{{y - 2}}\)
\(y - 2 = \frac{1}{{x + 3}}\) M1
Note: Award M1 for attempting to make y the subject.
\({f^{ - 1}}(x) = 2 + \frac{1}{{x + 3}}\left( { = \frac{{2x + 7}}{{x + 3}}} \right),{\text{ }}x \ne - 3\) A1A1
Note: Award A1 only if \({f^{ - 1}}(x)\) is seen. Award A1 for the domain.
[4 marks]
Examiners report
A Chocolate Shop advertises free gifts to customers that collect three vouchers. The vouchers are placed at random into 10% of all chocolate bars sold at this shop. Kati buys some of these bars and she opens them one at a time to see if they contain a voucher. Let \({\text{P}}(X = n)\) be the probability that Kati obtains her third voucher on the \(n{\text{th}}\) bar opened.
(It is assumed that the probability that a chocolate bar contains a voucher stays at 10% throughout the question.)
It is given that \({\text{P}}(X = n) = \frac{{{n^2} + an + b}}{{2000}} \times {0.9^{n - 3}}\) for \(n \geqslant 3,{\text{ }}n \in \mathbb{N}\).
Kati’s mother goes to the shop and buys \(x\) chocolate bars. She takes the bars home for Kati to open.
Show that \({\text{P}}(X = 3) = 0.001\) and \({\text{P}}(X = 4) = 0.0027\).
Find the values of the constants \(a\) and \(b\).
Deduce that \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n - 1)}} = \frac{{0.9(n - 1)}}{{n - 3}}\) for \(n > 3\).
(i) Hence show that \(X\) has two modes \({m_1}\) and \({m_2}\).
(ii) State the values of \({m_1}\) and \({m_2}\).
Determine the minimum value of \(x\) such that the probability Kati receives at least one free gift is greater than 0.5.
Markscheme
\({\text{P}}(X = 3) = {(0.1)^3}\) A1
\( = 0.001\) AG
\({\text{P}}(X = 4) = {\text{P}}(VV\bar VV) + {\text{P}}(V\bar VVV) + {\text{P}}(\bar VVVV)\) (M1)
\( = 3 \times {(0.1)^3} \times 0.9\) (or equivalent) A1
\( = 0.0027\) AG
[3 marks]
METHOD 1
attempting to form equations in \(a\) and \(b\) M1
\(\frac{{9 + 3a + b}}{{2000}} = \frac{1}{{1000}}{\text{ }}(3a + b = - 7)\) A1
\(\frac{{16 + 4a + b}}{{2000}} \times \frac{9}{{10}} = \frac{{27}}{{10\,000}}{\text{ }}(4a + b = - 10)\) A1
attempting to solve simultaneously (M1)
\(a = - 3,{\text{ }}b = 2\) A1
METHOD 2
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n - 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n - 3}}\) M1
\( = \frac{{(n - 1)(n - 2)}}{{2000}} \times {0.9^{n - 3}}\) (M1)A1
\( = \frac{{{n^2} - 3n + 2}}{{2000}} \times {0.9^{n - 3}}\) A1
\(a = - 3,b = 2\) A1
Note: Condone the absence of \({0.9^{n - 3}}\) in the determination of the values of \(a\) and \(b\).
[5 marks]
METHOD 1
EITHER
\({\text{P}}(X = n) = \frac{{{n^2} - 3n + 2}}{{2000}} \times {0.9^{n - 3}}\) (M1)
OR
\({\text{P}}(X = n) = \left( {\begin{array}{*{20}{c}} {n - 1} \\ 2 \end{array}} \right) \times {0.1^3} \times {0.9^{n - 3}}\) (M1)
THEN
\( = \frac{{(n - 1)(n - 2)}}{{2000}} \times {0.9^{n - 3}}\) A1
\({\text{P}}(X = n - 1) = \frac{{(n - 2)(n - 3)}}{{2000}} \times {0.9^{n - 4}}\) A1
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n - 1)}} = \frac{{(n - 1)(n - 2)}}{{(n - 2)(n - 3)}} \times 0.9\) A1
\( = \frac{{0.9(n - 1)}}{{n - 3}}\) AG
METHOD 2
\(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n - 1)}} = \frac{{\frac{{{n^2} - 3n + 2}}{{2000}} \times {{0.9}^{n - 3}}}}{{\frac{{{{(n - 1)}^2} - 3(n - 1) + 2}}{{2000}} \times {{0.9}^{n - 4}}}}\) (M1)
\( = \frac{{0.9({n^2} - 3n + 2)}}{{({n^2} - 5n + 6)}}\) A1A1
Note: Award A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{0.9(n - 1)(n - 2)}}{{(n - 2)(n - 3)}}\) A1
\( = \frac{{0.9(n - 1)}}{{n - 3}}\) AG
[4 marks]
(i) attempting to solve \(\frac{{0.9(n - 1)}}{{n - 3}} = 1\) for \(n\) M1
\(n = 21\) A1
\(\frac{{0.9(n - 1)}}{{n - 3}} < 1 \Rightarrow n > 21\) R1
\(\frac{{0.9(n - 1)}}{{n - 3}} > 1 \Rightarrow n < 21\) R1
\(X\) has two modes AG
Note: Award R1R1 for a clearly labelled graphical representation of the two inequalities (using \(\frac{{{\text{P}}(X = n)}}{{{\text{P}}(X = n - 1)}}\)).
(ii) the modes are 20 and 21 A1
[5 marks]
METHOD 1
\(Y \sim {\text{B}}(x,{\text{ }}0.1)\) (A1)
attempting to solve \({\text{P}}(Y \geqslant 3) > 0.5\) (or equivalent eg \(1 - {\text{P}}(Y \leqslant 2) > 0.5\)) for \(x\) (M1)
Note: Award (M1) for attempting to solve an equality (obtaining \(x = 26.4\)).
\(x = 27\) A1
METHOD 2
\(\sum\limits_{n = 0}^x {{\text{P}}(X = n) > 0.5} \) (A1)
attempting to solve for \(x\) (M1)
\(x = 27\) A1
[3 marks]
Examiners report
A function \(f\) is defined by \(f(x) = (x + 1)(x-1)(x-5),{\text{ }}x \in \mathbb{R}\).
Find the values of \(x\) for which \(f(x) < \left| {f(x)} \right|\).
A function \(g\) is defined by \(g(x) = {x^2} + x - 6,{\text{ }}x \in \mathbb{R}\).
Find the values of \(x\) for which \(g(x) < \frac{1}{{g(x)}}\).
Markscheme
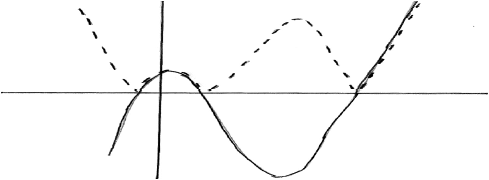
as roots of \(f(x) = 0\) are \( - 1,{\text{ }}1,{\text{ }}5\) (M1)
solution is \(\left] { - \infty ,{\text{ }} - 1} \right[ \cup \left] {1,{\text{ }}5} \right[\;\;\;(x < - 1\;\;\;{\text{or}}\;\;\;1 < x < 5)\) A1A1
Note: Award A1A0 for closed intervals.
[3 marks]
METHOD 1
\(\left( {{\text{graphs of }}g(x){\text{ and }}\frac{1}{{g(x)}}} \right)\)
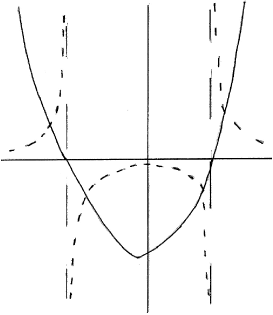
roots of \(g(x) = 0\) are \( - 3\) and 2 (M1)(A1)
Notes: Award M1 if quadratic graph is drawn or two roots obtained.
Roots may be indicated anywhere eg asymptotes on graph or in inequalities below.
the intersections of the graphs \(g(x)\) and of \(1/g(x)\)
are \( - 3.19,{\text{ }} - 2.79,{\text{ }}1.79,{\text{ 2.19}}\) (M1)(A1)
Note: Award A1 for at least one of the values above seen anywhere.
solution is \(\left] { - 3.19,{\text{ }} - 3} \right[ \cup \left] { - 2.79,{\text{ }}1.79} \right[ \cup \left] {2,{\text{ }}2.19} \right[\)
\(( - 3.19 < x < - 3\;\;\;{\text{or}}\;\;\; - 2.79 < x < 1.79\;\;\;{\text{or}}\;\;\;2 < x < 2.19)\) A1A1A1
Note: Award A1A1A0 for closed intervals.
METHOD 2
\(\left( {{\text{graph of }}g(x) - \frac{1}{{g(x)}}} \right)\)
asymptotes at \(x = - 3\) and \(x = 2\) (M1)(A1)
Note: May be indicated on the graph.
roots of graph are \( - 3.19,{\text{ }} - 2.79,{\text{ }}1.79,{\text{ }}2.19\) (M1)(A1)
Note: Award A1 for at least one of the values above seen anywhere.
solution is (when graph is negative)
\(\left] { - 3.19,{\text{ }} - 3} \right[ \cup \left] { - 2.79,{\text{ }}1.79} \right[ \cup \left] {2,{\text{ }}2.19} \right[\)
\(( - 3.19 < x < - 3\;\;\;{\text{or}}\;\;\; - 2.79 < x < 1.79\;\;\;{\text{or}}\;\;\;2 < x < 2.19)\) A1A1A1
Note: Award A1A1A0 for closed intervals.
[7 marks]
Total [10 marks]
Examiners report
In general part (a) was performed correctly, with the vast majority of candidates stating the correct open intervals as required.
In part (b) many candidates scored a few marks by just finding intersection points and equations of asymptotes; many other candidates showed difficulties in manipulating inequalities and ignored the fact that the quantities could be negative. Candidates that used the graph well managed to achieve full marks. Unfortunately many sketches were very crudely drawn hence they were of limited value for assessment purposes.
Consider the function \(f(x) = \frac{{\sqrt x }}{{\sin x}},{\text{ }}0 < x < \pi \).
Consider the region bounded by the curve \(y = f(x)\), the \(x\)-axis and the lines \(x = \frac{\pi }{6},{\text{ }}x = \frac{\pi }{3}\).
Show that the \(x\)-coordinate of the minimum point on the curve \(y = f(x)\) satisfies the equation \(\tan x = 2x\).
Determine the values of \(x\) for which \(f(x)\) is a decreasing function.
Sketch the graph of \(y = f(x)\) showing clearly the minimum point and any asymptotic behaviour.
Find the coordinates of the point on the graph of \(f\) where the normal to the graph is parallel to the line \(y = - x\).
This region is now rotated through \(2\pi \) radians about the \(x\)-axis. Find the volume of revolution.
Markscheme
attempt to use quotient rule or product rule M1
\(f’(x) = \frac{{\sin x\left( {\frac{1}{2}{x^{ - \frac{1}{2}}}} \right) - \sqrt x \cos x}}{{{{\sin }^2}x}}{\text{ }}\left( { = \frac{1}{{2\sqrt x \sin x}} - \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}} \right)\) A1A1
Note: Award A1 for \(\frac{1}{{2\sqrt x \sin x}}\) or equivalent and A1 for \( - \frac{{\sqrt x \cos x}}{{{{\sin }^2}x}}\) or equivalent.
setting \(f’(x) = 0\) M1
\(\frac{{\sin x}}{{2\sqrt x }} - \sqrt x \cos x = 0\)
\(\frac{{\sin x}}{{2\sqrt x }} = \sqrt x \cos x\) or equivalent A1
\(\tan x = 2x\) AG
[5 marks]
\(x = 1.17\)
\(0 < x \leqslant 1.17\) A1A1
Note: Award A1 for \(0 < x\) and A1 for \(x \leqslant 1.17\). Accept \(x < 1.17\).
[2 marks]

concave up curve over correct domain with one minimum point above the \(x\)-axis. A1
approaches \(x = 0\) asymptotically A1
approaches \(x = \pi \) asymptotically A1
Note: For the final A1 an asymptote must be seen, and \(\pi \) must be seen on the \(x\)-axis or in an equation.
[3 marks]
\(f’(x){\text{ }}\left( { = \frac{{\sin x\left( {\frac{1}{2}{x^{ - \frac{1}{2}}}} \right) - \sqrt x \cos x}}{{{{\sin }^2}x}}} \right) = 1\) (A1)
attempt to solve for \(x\) (M1)
\(x = 1.96\) A1
\(y = f(1.96 \ldots )\)
\( = 1.51\) A1
[4 marks]
\(V = \pi \int_{\frac{\pi }{6}}^{\frac{\pi }{3}} {\frac{{x{\text{d}}x}}{{{{\sin }^2}x}}} \) (M1)(A1)
Note: M1 is for an integral of the correct squared function (with or without limits and/or \(\pi \)).
\( = 2.68{\text{ }}( = 0.852\pi )\) A1
[3 marks]
Examiners report
Particle A moves such that its velocity \(v{\text{ m}}{{\text{s}}^{ - 1}}\), at time t seconds, is given by \(v(t) = \frac{t}{{12 + {t^4}}},{\text{ }}t \geqslant 0\).
Particle B moves such that its velocity \(v{\text{ m}}{{\text{s}}^{ - 1}}\) is related to its displacement \(s{\text{ m}}\), by the equation \(v(s) = \arcsin \left( {\sqrt s } \right)\).
Sketch the graph of \(y = v(t)\). Indicate clearly the local maximum and write down its coordinates.
Use the substitution \(u = {t^2}\) to find \(\int {\frac{t}{{12 + {t^4}}}{\text{d}}t} \).
Find the exact distance travelled by particle \(A\) between \(t = 0\) and \(t = 6\) seconds.
Give your answer in the form \(k\arctan (b),{\text{ }}k,{\text{ }}b \in \mathbb{R}\).
Find the acceleration of particle B when \(s = 0.1{\text{ m}}\).
Markscheme
(a)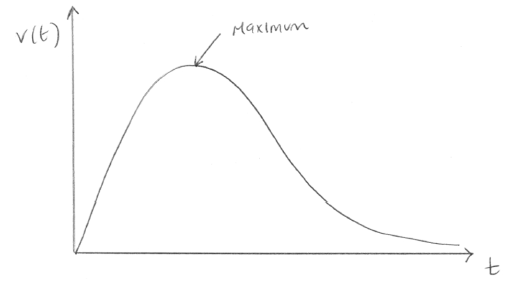 A1
A1
A1 for correct shape and correct domain
\((1.41,{\text{ }}0.0884){\text{ }}\left( {\sqrt 2 ,{\text{ }}\frac{{\sqrt 2 }}{{16}}} \right)\) A1
[2 marks]
EITHER
\(u = {t^2}\)
\(\frac{{{\text{d}}u}}{{{\text{d}}t}} = 2t\) A1
OR
\(t = {u^{\frac{1}{2}}}\)
\(\frac{{{\text{d}}t}}{{{\text{d}}u}} = \frac{1}{2}{u^{ - \frac{1}{2}}}\) A1
THEN
\(\int {\frac{t}{{12 + {t^4}}}{\text{d}}t = \frac{1}{2}\int {\frac{{{\text{d}}u}}{{12 + {u^2}}}} } \) M1
\( = \frac{1}{{2\sqrt {12} }}\arctan \left( {\frac{u}{{\sqrt {12} }}} \right)( + c)\) M1
\( = \frac{1}{{4\sqrt 3 }}\arctan \left( {\frac{{{t^2}}}{{2\sqrt 3 }}} \right)( + c)\) or equivalent A1
[4 marks]
\(\int_0^6 {\frac{t}{{12 + {t^4}}}{\text{d}}t} \) (M1)
\( = \left[ {\frac{1}{{4\sqrt 3 }}\arctan \left( {\frac{{{t^2}}}{{2\sqrt 3 }}} \right)} \right]_0^6\) M1
\( = \frac{1}{{4\sqrt 3 }}\left( {\arctan \left( {\frac{{36}}{{2\sqrt 3 }}} \right)} \right){\text{ }}\left( { = \frac{1}{{4\sqrt 3 }}\left( {\arctan \left( {\frac{{18}}{{\sqrt 3 }}} \right)} \right)} \right){\text{ (m)}}\) A1
Note: Accept \(\frac{{\sqrt 3 }}{{12}}\arctan \left( {6\sqrt 3 } \right)\) or equivalent.
[3 marks]
\(\frac{{{\text{d}}v}}{{{\text{d}}s}} = \frac{1}{{2\sqrt {s(1 - s)} }}\) (A1)
\(a = v\frac{{{\text{d}}v}}{{{\text{d}}s}}\)
\(a = \arcsin \left( {\sqrt s } \right) \times \frac{1}{{2\sqrt {s(1 - s)} }}\) (M1)
\(a = \arcsin \left( {\sqrt {0.1} } \right) \times \frac{1}{{2\sqrt {0.1 \times 0.9} }}\)
\(a = 0.536{\text{ (m}}{{\text{s}}^{ - 2}})\) A1
[3 marks]
Examiners report
Find the values of \(k\) such that the equation \({x^3} + {x^2} - x + 2 = k\) has three distinct real solutions.
Markscheme
from GDC, sketch a relevant graph A1
maximum: \(y = 3\) or (–1, 3) A1
minimum: \(y = 1.81\) or (0.333, 1.81) \(\left( {{\text{or }}y = \frac{{49}}{{27}}{\text{ or }}\left( {\frac{1}{3},\frac{{49}}{{27}}} \right)} \right)\) A1
hence, \(1.81 < k < 3\) A1A1 N3
Note: Award A1 for \(1.81 \leqslant k \leqslant 3\) .
[5 marks]
Examiners report
Responses to this question were surprisingly poor. Few candidates recognised that the easier way to answer the question was to use a graph on the GDC. Many candidates embarked on fruitless algebraic manipulation which led nowhere.
When \({x^2} + 4x - b\) is divided by \(x - a\) the remainder is 2.
Given that \(a,{\text{ }}b \in \mathbb{R}\), find the smallest possible value for \(b\).
Markscheme
\({a^2} + 4a - b = 2\) M1A1
EITHER
\({a^2} + 4a - (b + 2) = 0\)
as \(a\) is real \( \Rightarrow 16 + 4(b + 2) \geqslant 0\) M1A1
OR
\(b = {a^2} + 4a - 2\) M1
\( = {(a + 2)^2} - 6\) (A1)
THEN
\(b \geqslant - 6\)
hence smallest possible value for \(b\) is \( - 6\) A1
[5 marks]
Examiners report
For quite a difficult question, there were many good solutions for this, including many different methods. It was disturbing to see how many students did not seem to be aware of the remainder theorem, instead choosing to divide the polynomial.
Find the set of values of \(k\) that satisfy the inequality \({k^2} - k - 12 < 0\).
The triangle ABC is shown in the following diagram. Given that \(\cos B < \frac{1}{4}\), find the range of possible values for AB.

Markscheme
\({k^2} - k - 12 < 0\)
\((k - 4)(k + 3) < 0\) (M1)
\( - 3 < k < 4\) A1
[2 marks]
\(\cos B = \frac{{{2^2} + {c^2} - {4^2}}}{{4c}}{\text{ }}({\text{or }}16 = {2^2} + {c^2} - 4c\cos B)\) M1
\( \Rightarrow \frac{{{c^2} - 12}}{{4c}} < \frac{1}{4}\) A1
\( \Rightarrow {c^2} - c - 12 < 0\)
from result in (a)
\(0 < {\text{AB}} < 4\) or \( - 3 < {\text{AB}} < 4\) (A1)
but AB must be at least 2
\( \Rightarrow 2 < {\text{AB}} < 4\) A1
Note: Allow \( \leqslant {\text{AB}}\) for either of the final two A marks.
[4 marks]
Examiners report
The equation \({x^2} - 5x - 7 = 0\) has roots \(\alpha \) and \(\beta \). The equation \({x^2} + px + q = 0\) has roots \(\alpha + 1\) and \(\beta + 1\). Find the value of \(p\) and the value of \(q\).
Markscheme
METHOD 1
\(\alpha + \beta = 5,\,\,\alpha \beta = - 7\) (M1)(A1)
Note: Award M1A0 if only one equation obtained.
\(\left( {\alpha + 1} \right) + \left( {\beta + 1} \right) = 5 + 2 = 7\) A1
\(\left( {\alpha + 1} \right)\left( {\beta + 1} \right) = \alpha \beta + \left( {\alpha + \beta } \right) + 1\) (M1)
\( = - 7 + 5 + 1 = - 1\)
\(p = - 7,\,\,q = - 1\) A1A1
METHOD 2
\(\alpha = \frac{{5 + \sqrt {53} }}{2} = 6.1 \ldots {\text{;}}\,\,\beta = \frac{{5 - \sqrt {53} }}{2} = - 1.1 \ldots \) (M1)(A1)
\(\alpha + 1 = \frac{{7 + \sqrt {53} }}{2} = 7.1 \ldots {\text{;}}\,\,\beta + 1 = \frac{{7 - \sqrt {53} }}{2} = - 0.1 \ldots \) A1
\(\left( {x - 7.14 \ldots } \right)\left( {x + 0.14 \ldots } \right) = {x^2} - 7x - 1\) (M1)
\(p = - 7,\,\,q = - 1\) A1A1
Note: Exact answers only.
[6 marks]
Examiners report
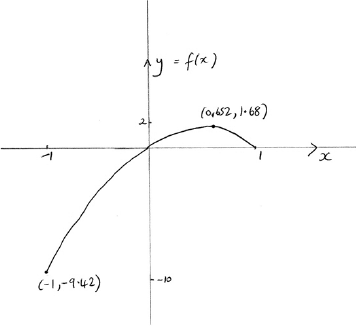
Consider the function \(f\) defined by \(f(x) = 3x\arccos (x)\) where \( - 1 \leqslant x \leqslant 1\).
Sketch the graph of \(f\) indicating clearly any intercepts with the axes and the coordinates of any local maximum or minimum points.
State the range of \(f\).
Solve the inequality \(\left| {3x\arccos (x)} \right| > 1\).
Markscheme
correct shape passing through the origin and correct domain A1
Note: Endpoint coordinates are not required. The domain can be indicated by \( - 1\) and 1 marked on the axis.
\((0.652,{\text{ }}1.68)\) A1
two correct intercepts (coordinates not required) A1
Note: A graph passing through the origin is sufficient for \((0,{\text{ }}0)\).
[3 marks]
\([-9.42,{\text{ }}1.68]{\text{ }}({\text{or }} - 3\pi ,{\text{ }}1.68])\) A1A1
Note: Award A1A0 for open or semi-open intervals with correct endpoints. Award A1A0 for closed intervals with one correct endpoint.
[2 marks]
attempting to solve either \(\left| {3x\arccos (x)} \right| > 1\) (or equivalent) or \(\left| {3x\arccos (x)} \right| = 1\) (or equivalent) (eg. graphically) (M1)
\(x = - 0.189,{\text{ }}0.254,{\text{ }}0.937\) (A1)
\( - 1 \leqslant x < - 0.189{\text{ or }}0.254 < x < 0.937\) A1A1
Note: Award A0 for \(x < - 0.189\).
[4 marks]
Examiners report
A polynomial \(p(x)\) with real coefficients is of degree five. The equation \(p(x) = 0\) has a complex root 2 + i. The graph of \(y = p(x)\) has the x-axis as a tangent at (2, 0) and intersects the coordinate axes at (−1, 0) and (0, 4).
Find \(p(x)\) in factorised form with real coefficients.
Markscheme
other root is 2 – i (A1)
a quadratic factor is therefore \((x - 2 + i)(x - 2 - i)\) (M1)
\( = {x^2} - 4x + 5\) A1
x + 1 is a factor A1
\({(x - 2)^2}\) is a factor A1
\(p(x) = a(x + 1){(x - 2)^2}({x^2} - 4x + 5)\) (M1)
\(p(0) = 4 \Rightarrow a = \frac{1}{5}\) A1
\(p(x) = \frac{1}{5}(x + 1){(x - 2)^2}({x^2} - 4x + 5)\)
[7 marks]
Examiners report
Whilst most candidates knew that another root was \(2 - {\text{i}}\) , much fewer were able to find the quadratic factor. Surprisingly few candidates knew that \(\left( {x - 2} \right)\) must be a repeated factor and less surprisingly many did not recognise that the whole expression needed to be multiplied by \(\frac{1}{5}\).
In the quadratic equation \(7{x^2} - 8x + p = 0,{\text{ }}(p \in \mathbb{Q})\), one root is three times the other root.
Find the value of \(p\).
Markscheme
METHOD 1
let roots be \(\alpha \) and \(3\alpha \) (M1)
sum of roots \((4\alpha ) = \frac{8}{7}\) M1
\( \Rightarrow \alpha = \frac{2}{7}\) A1
EITHER
product of roots \((3{\alpha ^2}) = \frac{p}{7}\) M1
\(p = 21{\alpha ^2} = 21 \times \frac{4}{{49}}\)
OR
\(7{\left( {\frac{2}{7}} \right)^2} - 8\left( {\frac{2}{7}} \right) + p = 0\) M1
\(\frac{4}{7} - \frac{{16}}{7} + p = 0\)
THEN
\( \Rightarrow p = \frac{{12}}{7}{\text{ }}( = 1.71)\) A1
METHOD 2
\(x = \frac{{8 \pm \sqrt {64 - 28p} }}{{14}}\) (M1)
\(\frac{{8 + \sqrt {64 - 28p} }}{{14}} = 3\left( {\frac{{8 - \sqrt {64 - 28p} }}{{14}}} \right)\) M1A1
\(8 + \sqrt {64 - 28p} = 24 - 3\sqrt {64 - 28p} \Rightarrow \sqrt {64 - 28p} = 4\) (M1)
\(p = \frac{{12}}{7}{\text{ }}( = 1.71)\) A1
[5 marks]
Examiners report
Given that the graph of \(y = {x^3} - 6{x^2} + kx - 4\) has exactly one point at which the gradient is zero, find the value of k .
Markscheme
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 3{x^2} - 12x + k\) M1A1
For use of discriminant \({b^2} - 4ac = 0\) or completing the square \(3{(x - 2)^2} + k - 12\) (M1)
\(144 - 12k = 0\) (A1)
Note: Accept trial and error, sketches of parabolas with vertex (2,0) or use of second derivative.
\(k = 12\) A1
[5 marks]
Examiners report
Generally candidates answer this question well using a diversity of methods. Surprisingly, a small number of candidates were successful in answering this question using the discriminant of the quadratic and in many cases reverted to trial and error to obtain the correct answer.
The vectors a and b are such that a \( = (3\cos \theta + 6)\)i \( + 7\) j and b \( = (\cos \theta - 2)\)i \( + (1 + \sin \theta )\)j.
Given that a and b are perpendicular,
show that \(3{\sin ^2}\theta - 7\sin \theta + 2 = 0\);
find the smallest possible positive value of \(\theta \).
Markscheme
attempting to form \((3\cos \theta + 6)(\cos \theta - 2) + 7(1 + \sin \theta ) = 0\) M1
\(3{\cos ^2}\theta - 12 + 7\sin \theta + 7 = 0\) A1
\(3\left( {1 - {{\sin }^2}\theta } \right) + 7\sin \theta - 5 = 0\) M1
\(3{\sin ^2}\theta - 7\sin \theta + 2 = 0\) AG
[3 marks]
attempting to solve algebraically (including substitution) or graphically for \(\sin \theta \) (M1)
\(\sin \theta = \frac{1}{3}\) (A1)
\(\theta = 0.340{\text{ }}( = 19.5^\circ )\) A1
[3 marks]
Examiners report
Part (a) was very well done. Most candidates were able to use the scalar product and \({\cos ^2}\theta = 1 - {\sin ^2}\theta \) to show the required result.
Part (b) was reasonably well done. A few candidates confused ‘smallest possible positive value’ with a minimum function value. Some candidates gave \(\theta = 0.34\) as their final answer.
The function f is of the form \(f(x) = \frac{{x + a}}{{bx + c}}\), \(x \ne - \frac{c}{b}\). Given that the graph of f has asymptotes x = −4 and y = −2 , and that the point \(\left( {\frac{2}{3},{\text{ }}1} \right)\) lies on the graph, find the values of a , b and c .
Markscheme
vertical asymptote \(x = - 4 \Rightarrow - 4b + c = 0\) M1
horizontal asymptote \(y = - 2 \Rightarrow \frac{1}{b} = - 2\) M1
\(b = - \frac{1}{2}{\text{ and }}c = - 2\) A1A1
\(1 = \frac{{\frac{2}{3} + a}}{{ - \frac{1}{2} \times \frac{2}{3} - 2}}\) M1
\(a = - 3\) A1
[6 marks]
Examiners report
The graph of \(y = \ln (x)\) is transformed into the graph of \(y = \ln \left( {2x + 1} \right)\) .
Describe two transformations that are required to do this.
Solve \(\ln \left( {2x + 1} \right) > 3\cos (x)\), \(x \in [0,10]\).
Markscheme
EITHER
translation of \( - \frac{1}{2}\) parallel to the \(x\)-axis
stretch of a scale factor of \(\frac{1}{2}\) parallel to the \(x\)-axis A1A1
OR
stretch of a scale factor of \(\frac{1}{2}\) parallel to the \(x\)-axis
translation of \( - 1\) parallel to the \(x\)-axis A1A1
Note: Accept clear alternative terminologies for either transformation.
[2 marks]
EITHER
\(1.16 < x < 5.71 \cup 6.75 < x \leqslant 10\) A1A1A1A1
OR
]\(1.16\), \(5.71\)[ \(\cup\) ]\(6.75\), \(10\)] A1A1A1A1
Note: Award A1 for 1 intersection value, A1 for the other 2, A1A1 for the intervals.
[6 marks]
Examiners report
This question was well done by many candidates. It would appear, however, that few candidates were aware of the standard terminology – Stretch and Translation - used to describe the relevant graph transformations. Most made good use of a GDC to find the critical points and to help in deciding on the correct intervals. A significant minority failed to note \(x = 10\) as an endpoint.
This question was well done by many candidates. It would appear, however, that few candidates were aware of the standard terminology – Stretch and Translation - used to describe the relevant graph transformations. Most made good use of a GDC to find the critical points and to help in deciding on the correct intervals. A significant minority failed to note \(x = 10\) as an endpoint.
The arithmetic sequence \(\{ {u_n}:n \in {\mathbb{Z}^ + }\} \) has first term \({u_1} = 1.6\) and common difference d = 1.5. The geometric sequence \(\{ {v_n}:n \in {\mathbb{Z}^ + }\} \) has first term \({v_1} = 3\) and common ratio r = 1.2.
Find an expression for \({u_n} - {v_n}\) in terms of n.
Determine the set of values of n for which \({u_n} > {v_n}\).
Determine the greatest value of \({u_n} - {v_n}\). Give your answer correct to four significant figures.
Markscheme
\({u_n} - {v_n} = 1.6 + (n - 1) \times 1.5 - 3 \times {1.2^{n - 1}}{\text{ }}( = 1.5n + 0.1 - 3 \times {1.2^{n - 1}})\) A1A1
[2 marks]
attempting to solve \({u_n} > {v_n}\) numerically or graphically. (M1)
\(n = 2.621 \ldots ,9.695 \ldots \) (A1)
So \(3 \leqslant n \leqslant 9\) A1
[3 marks]
The greatest value of \({u_n} - {v_n}\) is 1.642. A1
Note: Do not accept 1.64.
[1 mark]
Examiners report
In part (a), most candidates were able to express \({u_n}\) and \({v_n}\) correctly and hence obtain a correct expression for \({u_n} - {v_n}\). Some candidates made careless algebraic errors when unnecessarily simplifying \({u_n}\) while other candidates incorrectly stated \({v_n}\) as \(3{(1.2)^n}\).
In parts (b) and (c), most candidates treated n as a continuous variable rather than as a discrete variable. Candidates should be aware that a GDC’s table feature can be extremely useful when attempting such question types.
In parts (b) and (c), most candidates treated n as a continuous variable rather than as a discrete variable. Candidates should be aware that a GDC’s table feature can be extremely useful when attempting such question types. In part (c), a number of candidates attempted to find the maximum value of n rather than attempting to find the maximum value of \({u_n} - {v_n}\).
A particle moves in a straight line, its velocity \(v{\text{ m}}{{\text{s}}^{ - 1}}\) at time \(t\) seconds is given by \(v = 9t - 3{t^2},{\text{ }}0 \le t \le 5\).
At time \(t = 0\), the displacement \(s\) of the particle from an origin \(O\) is 3 m.
Find the displacement of the particle when \(t = 4\).
Sketch a displacement/time graph for the particle, \(0 \le t \le 5\), showing clearly where the curve meets the axes and the coordinates of the points where the displacement takes greatest and least values.
For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Given further that \(s = 16.5\) when \(t = 7.5\), find the values of \(a\) and \(b\).
For \(t > 5\), the displacement of the particle is given by \(s = a + b\cos \frac{{2\pi t}}{5}\) such that \(s\) is continuous for all \(t \ge 0\).
Find the times \({t_1}\) and \({t_2}(0 < {t_1} < {t_2} < 8)\) when the particle returns to its starting point.
Markscheme
METHOD 1
\(s = \int {(9t - 3{t^2}){\text{d}}t = \frac{9}{2}{t^2} - {t^3}( + c)} \) (M1)
\(t = 0,{\text{ }}s = 3 \Rightarrow c = 3\) (A1)
\(t = 4 \Rightarrow s = 11\) A1
METHOD 2
\(s = 3 + \int_0^4 {(9t - 3{t^2}){\text{d}}t} \) (M1)(A1)
\(s = 11\) A1
[3 marks]
correct shape over correct domain A1
maximum at \((3,{\text{ }}16.5)\) A1
\(t\) intercept at \(4.64\), \(s\) intercept at \(3\) A1
minimum at \((5,{\text{ }} - 9.5)\) A1
[5 marks]
\( - 9.5 = a + b\cos 2\pi \)
\(16.5 = a + b\cos 3\pi \) (M1)
Note: Only award M1 if two simultaneous equations are formed over the correct domain.
\(a = \frac{7}{2}\) A1
\(b = - 13\) A1
[3 marks]
at \({t_1}\):
\(3 + \frac{9}{2}{t^2} - {t^3} = 3\) (M1)
\({t^2}\left( {\frac{9}{2} - t} \right) = 0\)
\({t_1} = \frac{9}{2}\) A1
solving \(\frac{7}{2} - 13\cos \frac{{2\pi t}}{5} = 3\) (M1)
\({\text{GDC}} \Rightarrow {t_2} = 6.22\) A1
Note: Accept graphical approaches.
[4 marks]
Total [15 marks]
Examiners report
Prove that the equation \(3{x^2} + 2kx + k - 1 = 0\) has two distinct real roots for all values of \(k \in \mathbb{R}\).
Find the value of k for which the two roots of the equation are closest together.
Markscheme
\(\Delta = {b^2} - 4ac = 4{k^2} - 4 \times 3 \times (k - 1) = 4{k^2} - 12k + 12\) M1A1
Note: Award M1A1 if expression seen within quadratic formula.
EITHER
\(144 - 4 \times 4 \times 12 < 0\) M1
\(\Delta \) always positive, therefore the equation always has two distinct real roots R1
(and cannot be always negative as \(a > 0\))
OR
sketch of \(y = 4{k^2} - 12k + 12\) or \(y = {k^2} - 3k + 3\) not crossing the x-axis M1
\(\Delta \) always positive, therefore the equation always has two distinct real roots R1
OR
write \(\Delta \) as \(4{(k - 1.5)^2} + 3\) M1
\(\Delta \) always positive, therefore the equation always has two distinct real roots R1
[4 marks]
closest together when \(\Delta \) is least (M1)
minimum value occurs when k = 1.5 (M1)A1
[3 marks]
Examiners report
Most candidates were able to find the discriminant (sometimes only as part of the quadratic formula) but fewer were able to explain satisfactorily why there were two distinct roots.
Most candidates were able to find the discriminant (sometimes only as part of the quadratic formula) but fewer were able to explain satisfactorily why there were two distinct roots. Only the better candidates were able to give good answers to part (b).
Farmer Bill owns a rectangular field, 10 m by 4 m. Bill attaches a rope to a wooden post at one corner of his field, and attaches the other end to his goat Gruff.
Given that the rope is 5 m long, calculate the percentage of Bill’s field that Gruff is able to graze. Give your answer correct to the nearest integer.
Bill replaces Gruff’s rope with another, this time of length \(a,{\text{ }}4 < a < 10\), so that Gruff can now graze exactly one half of Bill’s field.
Show that \(a\) satisfies the equation
\[{a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} - 16} = 40.\]
Find the value of \(a\).
Markscheme
EITHER
area of triangle \( = \frac{1}{2} \times 3 \times 4\;\;\;( = 6)\) A1
area of sector \( = \frac{1}{2}\arcsin \left( {\frac{4}{5}} \right) \times {5^2}\;\;\;( = 11.5911 \ldots )\) A1
OR
\(\int_0^4 {\sqrt {25 - {x^2}} {\text{d}}x} \) M1A1
THEN
total area \( = 17.5911 \ldots {\text{ }}{{\text{m}}^2}\) (A1)
percentage \( = \frac{{17.5911 \ldots }}{{40}} \times 100 = 44\% \) A1
[4 marks]
METHOD 1

area of triangle \( = \frac{1}{2} \times 4 \times \sqrt {{a^2} - 16} \) A1
\(\theta = \arcsin \left( {\frac{4}{a}} \right)\) (A1)
area of sector \( = \frac{1}{2}{r^2}\theta = \frac{1}{2}{a^2}\arcsin \left( {\frac{4}{a}} \right)\) A1
therefore total area \( = 2\sqrt {{a^2} - 16} + \frac{1}{2}{a^2}\arcsin \left( {\frac{4}{a}} \right) = 20\) A1
rearrange to give: \({a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} - 16} = 40\) AG
METHOD 2
\(\int_0^4 {\sqrt {{a^2} - {x^2}} {\text{d}}x = 20} \) M1
use substitution \(x = a\sin \theta ,{\text{ }}\frac{{{\text{d}}x}}{{{\text{d}}\theta }} = a\cos \theta \)
\(\int_0^{\arcsin \left( {\frac{4}{a}} \right)} {{a^2}{{\cos }^2}\theta {\text{d}}\theta = 20} \)
\(\frac{{{a^2}}}{2}\int_0^{\arcsin \left( {\frac{4}{a}} \right)} {(\cos 2\theta + 1){\text{d}}\theta = 20} \) M1
\({a^2}\left[ {\left( {\frac{{\sin 2\theta }}{2} + \theta } \right)} \right]_0^{\arcsin \left( {\frac{4}{a}} \right)} = 40\) A1
\({a^2}\left[ {(\sin \theta \cos \theta + \theta } \right]_0^{\arcsin \left( {\frac{4}{a}} \right)} = 40\)
\({a^2}\arcsin \left( {\frac{4}{a}} \right) + {a^2}\left( {\frac{4}{a}} \right)\sqrt {\left( {1 - {{\left( {\frac{4}{a}} \right)}^2}} \right)} = 40\) A1
\({a^2}\arcsin \left( {\frac{4}{a}} \right) + 4\sqrt {{a^2} - 16} = 40\) AG
[4 marks]
solving using \({\text{GDC}} \Rightarrow a = 5.53{\text{ cm}}\) A2
[2 marks]
Total [10 marks]
Examiners report
The functions \(f\) and \(g\) are defined by
\[f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}}{2},{\text{ }}x \in \mathbb{R}\]
\[g(x) = \frac{{{{\text{e}}^x} - {{\text{e}}^{ - x}}}}{2},{\text{ }}x \in \mathbb{R}\]
Let \(h(x) = nf(x) + g(x)\) where \(n \in \mathbb{R},{\text{ }}n > 1\).
Let \(t(x) = \frac{{g(x)}}{{f(x)}}\).
(i) Show that \(\frac{1}{{4f(x) - 2g(x)}} = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\).
(ii) Use the substitution \(u = {{\text{e}}^x}\) to find \(\int_0^{\ln 3} {\frac{1}{{4f(x) - 2g(x)}}} {\text{d}}x\). Give your answer in the form \(\frac{{\pi \sqrt a }}{b}\) where \(a,{\text{ }}b \in {\mathbb{Z}^ + }\).
(i) By forming a quadratic equation in \({{\text{e}}^x}\), solve the equation \(h(x) = k\), where \(k \in {\mathbb{R}^ + }\).
(ii) Hence or otherwise show that the equation \(h(x) = k\) has two real solutions provided that \(k > \sqrt {{n^2} - 1} \) and \(k \in {\mathbb{R}^ + }\).
(i) Show that \(t'(x) = \frac{{{{[f(x)]}^2} - {{[g(x)]}^2}}}{{{{[f(x)]}^2}}}\) for \(x \in \mathbb{R}\).
(ii) Hence show that \(t'(x) > 0\) for \(x \in \mathbb{R}\).
Markscheme
(i) \(\frac{1}{{4\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}}{2}} \right) - 2\left( {\frac{{{{\text{e}}^x} - {{\text{e}}^{ - x}}}}{2}} \right)}}\) (M1)
\( = \frac{1}{{2({{\text{e}}^x} + {{\text{e}}^{ - x}}) - ({{\text{e}}^x} - {{\text{e}}^{ - x}})}}\) (A1)
\( = \frac{1}{{{{\text{e}}^x} + 3{{\text{e}}^{ - x}}}}\) A1
\( = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\) AG
(ii) \(u = {{\text{e}}^x} \Rightarrow {\text{d}}u = {{\text{e}}^x}{\text{d}}x\) A1
\(\int {\frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}{\text{d}}x = \int {\frac{1}{{{u^2} + 3}}{\text{d}}u} } \) M1
(when \(x = 0,{\text{ }}u = 1\) and when \(x = \ln 3,{\text{ }}u = 3\))
\(\int_1^3 {\frac{1}{{{u^2} + 3}}{\text{d}}u\left[ {\frac{1}{{\sqrt 3 }}\arctan \left( {\frac{u}{{\sqrt 3 }}} \right)} \right]_1^3} \) M1A1
\(\left( { = \left[ {\frac{1}{{\sqrt 3 }}\arctan \left( {\frac{{{{\text{e}}^x}}}{{\sqrt 3 }}} \right)} \right]_0^{\ln 3}} \right)\)
\( = \frac{{\pi \sqrt 3 }}{9} - \frac{{\pi \sqrt 3 }}{{18}}\) (M1)
\( = \frac{{\pi \sqrt 3 }}{{18}}\) A1
[9 marks]
(i) \((n + 1){{\text{e}}^{2x}} - 2k{{\text{e}}^x} + (n - 1) = 0\) M1A1
\({{\text{e}}^x} = \frac{{2k \pm \sqrt {4{k^2} - 4({n^2} - 1)} }}{{2(n + 1)}}\) M1
\(x = \ln \left( {\frac{{k \pm \sqrt {{k^2} - {n^2} + 1} }}{{n + 1}}} \right)\) M1A1
(ii) for two real solutions, we require \(k > \sqrt {{k^2} - {n^2} + 1} \) R1
and we also require \({k^2} - {n^2} + 1 > 0\) R1
\({k^2} > {n^2} - 1\) A1
\( \Rightarrow k > \sqrt {{n^2} - 1} {\text{ }}({\text{ }}k \in {\mathbb{R}^ + })\) AG
[8 marks]
METHOD 1
\(t(x) = \frac{{{{\text{e}}^x} - {{\text{e}}^{ - x}}}}{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}}\)
\(t'(x) = \frac{{{{({{\text{e}}^x} + {{\text{e}}^{ - x}})}^2} - {{({{\text{e}}^x} - {{\text{e}}^{ - x}})}^2}}}{{{{({{\text{e}}^x} + {{\text{e}}^{ - x}})}^2}}}\) M1A1
\(t'(x) = \frac{{{{\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}}{2}} \right)}^2} - {{\left( {\frac{{{{\text{e}}^x} - {{\text{e}}^{ - x}}}}{2}} \right)}^2}}}{{{{\left( {\frac{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}}{2}} \right)}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} - {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 2
\(t'(x) = \frac{{f(x)g'(x) = g(x)f'(x)}}{{{{\left[ {f(x)} \right]}^2}}}\) M1A1
\(g'(x) = f(x)\) and \(f'(x) = g(x)\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} - {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 3
\(t(x) = ({{\text{e}}^x} - {{\text{e}}^{ - x}}){({{\text{e}}^x} + {{\text{e}}^{ - x}})^{ - 1}}\)
\(t'(x) = 1 - \frac{{{{({{\text{e}}^x} - {{\text{e}}^{ - x}})}^2}}}{{{{({{\text{e}}^x} + {{\text{e}}^{ - x}})}^2}}}\) M1A1
\( = 1 - \frac{{{{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} - {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
METHOD 4
\(t'(x) = \frac{{g'(x)}}{{f(x)}} - \frac{{g(x)f'(x)}}{{{{\left[ {f(x)} \right]}^2}}}\) M1A1
\(g'(x) = f(x)\) and \(f'(x) = g(x)\) gives \(t'(x) = 1 - \frac{{{{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) A1
\( = \frac{{{{\left[ {f(x)} \right]}^2} - {{\left[ {g(x)} \right]}^2}}}{{{{\left[ {f(x)} \right]}^2}}}\) AG
(ii) METHOD 1
\({\left[ {f(x)} \right]^2} > {\left[ {g(x)} \right]^2}\) (or equivalent) M1A1
\({\left[ {f(x)} \right]^2} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
Note: Award as above for use of either \(f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}}{2}\) and \(g(x) = \frac{{{{\text{e}}^x} - {{\text{e}}^{ - x}}}}{2}\) or \({{\text{e}}^x} + {{\text{e}}^{ - x}}\) and \({{\text{e}}^x} - {{\text{e}}^{ - x}}\).
METHOD 2
\({\left[ {f(x)} \right]^2} - {\left[ {g(x)} \right]^2} = 1\) (or equivalent) M1A1
\({\left[ {f(x)} \right]^2} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
Note: Award as above for use of either \(f(x) = \frac{{{{\text{e}}^x} + {{\text{e}}^{ - x}}}}{2}\) and \(g(x) = \frac{{{{\text{e}}^x} - {{\text{e}}^{ - x}}}}{2}\) or \({{\text{e}}^x} + {{\text{e}}^{ - x}}\) and \({{\text{e}}^x} - {{\text{e}}^{ - x}}\).
METHOD 3
\(t'(x) = \frac{4}{{{{({{\text{e}}^x} + {{\text{e}}^{ - x}})}^2}}}\)
\({\left( {{{\text{e}}^x} + {{\text{e}}^{ - x}}} \right)^2} > 0\) M1A1
\(\frac{4}{{{{\left( {{{\text{e}}^x} + {{\text{e}}^{ - x}}} \right)}^2}}} > 0\) R1
hence \(t'(x) > 0,{\text{ }}x \in \mathbb{R}\) AG
[6 marks]
Examiners report
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
Part (a)(i) was reasonably well done with most candidates able to show that \(\frac{1}{{4f(x) - 2g(x)}} = \frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}\). In part (a)(ii), a number of candidates correctly used the required substitution to obtain \(\int {\frac{{{{\text{e}}^x}}}{{{{\text{e}}^{2x}} + 3}}{\text{d}}x = \int {\frac{1}{{{u^2} + 3}}{\text{d}}u} } \) but then thought that the antiderivative involved natural log rather than arctan.
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
In part (b)(i), a reasonable number of candidates were able to form a quadratic in \({{\text{e}}^x}\) (involving parameters \(n\) and \(k\)) and then make some progress towards solving for \({{\text{e}}^x}\) in terms of \(n\) and \(k\). Having got that far, a small number of candidates recognised to then take the natural logarithm of both sides and hence solve \(h(x) = k\) for \(\chi \). In part (b)(ii), a small number of candidates were able to show from their solutions to part (b)(i) or through the use of the discriminant that the equation \(h(x) = k\) has two real solutions provided that \(k > \sqrt {{k^2} - {n^2} + 1} \) and \(k > \sqrt {{n^2} - 1} \).
Parts (a) and (c) were accessible to the large majority of candidates. Candidates found part (b) considerably more challenging.
It was pleasing to see the number of candidates who attempted part (c). In part (c)(i), a large number of candidates were able to correctly apply either the quotient rule or the product rule to find \(t'(x)\). A smaller number of candidates were then able to show equivalence between the form of \(t'(x)\) they had obtained and the form of \(t'(x)\) required in the question. A pleasing number of candidates were able to exploit the property that \(f'(x) = g(x)\) and \(g'(x) = f(x)\). As with part (c)(i), part (c)(ii) could be successfully tackled in a number of ways. The best candidates offered concise logical reasoning to show that \(t'(x) > 0\) for \(x \in \mathbb{R}\).
Let the function \(f\) be defined by \(f(x) = \frac{{2 - {{\text{e}}^x}}}{{2{{\text{e}}^x} - 1}},{\text{ }}x \in D\).
Determine \(D\), the largest possible domain of \(f\).
Show that the graph of \(f\) has three asymptotes and state their equations.
Show that \(f'(x) = - \frac{{3{{\text{e}}^x}}}{{{{(2{{\text{e}}^x} - 1)}^2}}}\).
Use your answers from parts (b) and (c) to justify that \(f\) has an inverse and state its domain.
Find an expression for \({f^{ - 1}}(x)\).
Consider the region \(R\) enclosed by the graph of \(y = f(x)\) and the axes.
Find the volume of the solid obtained when \(R\) is rotated through \(2\pi \) about the \(y\)-axis.
Markscheme
attempting to solve either \(2{{\text{e}}^x} - 1 = 0\) or \(2{{\text{e}}^x} - 1 \ne 0\) for \(x\) (M1)
\(D = \mathbb{R}\backslash \left\{ { - \ln 2} \right\}\) (or equivalent eg \(x \ne - \ln 2\)) A1
Note: Accept \(D = \mathbb{R}\backslash \left\{ { - 0.693} \right\}\) or equivalent eg \(x \ne - 0.693\).
[2 marks]
considering \(\mathop {\lim }\limits_{x \to - \ln 2} f(x)\) (M1)
\(x = - \ln 2{\text{ }}(x = - 0.693)\) A1
considering one of \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) or \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) M1
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = - 2 \Rightarrow y = - 2\) A1
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \frac{1}{2} \Rightarrow y = - \frac{1}{2}\) A1
Note: Award A0A0 for \(y = - 2\) and \(y = - \frac{1}{2}\) stated without any justification.
[5 marks]
\(f'(x) = \frac{{ - {{\text{e}}^x}(2{{\text{e}}^x} - 1) - 2{{\text{e}}^x}(2 - {{\text{e}}^x})}}{{{{(2{{\text{e}}^x} - 1)}^2}}}\) M1A1A1
\( = - \frac{{3{{\text{e}}^x}}}{{{{(2{{\text{e}}^x} - 1)}^2}}}\) AG
[3 marks]
\(f'(x) < 0{\text{ (for all }}x \in D) \Rightarrow f\) is (strictly) decreasing R1
Note: Award R1 for a statement such as \(f'(x) \ne 0\) and so the graph of \(f\) has no turning points.
one branch is above the upper horizontal asymptote and the other branch is below the lower horizontal asymptote R1
\(f\) has an inverse AG
\( - \infty < x < - 2 \cup - \frac{1}{2} < x < \infty \) A2
Note: Award A2 if the domain of the inverse is seen in either part (d) or in part (e).
[4 marks]
\(x = \frac{{2 - {{\text{e}}^y}}}{{2{{\text{e}}^y} - 1}}\) M1
Note: Award M1 for interchanging \(x\) and \(y\) (can be done at a later stage).
\(2x{{\text{e}}^y} - x = 2 - {{\text{e}}^y}\) M1
\({{\text{e}}^y}(2x + 1) = x + 2\) A1
\({f^{ - 1}}(x) = \ln \left( {\frac{{x + 2}}{{2x + 1}}} \right){\text{ }}\left( {{f^{ - 1}}(x) = \ln (x + 2) - \ln (2x + 1)} \right)\) A1
[4 marks]
use of \(V = \pi \int_a^b {{x^2}{\text{d}}y} \) (M1)
\( = \pi \int_0^1 {{{\left( {\ln \left( {\frac{{y + 2}}{{2y + 1}}} \right)} \right)}^2}{\text{d}}y} \) (A1)(A1)
Note: Award (A1) for the correct integrand and (A1) for the limits.
\( = 0.331\) A1
[4 marks]
Examiners report
The graphs of \(y = {x^2}{{\text{e}}^{ - x}}\) and \(y = 1 - 2\sin x\) for \(2 \leqslant x \leqslant 7\) intersect at points A and B.
The x-coordinates of A and B are \({x_{\text{A}}}\) and \({x_{\text{B}}}\).
Find the value of \({x_{\text{A}}}\) and the value of \({x_{\text{B}}}\).
Find the area enclosed between the two graphs for \({x_{\mathbf{A}}} \leqslant x \leqslant {x_{\text{B}}}\).
Markscheme
\({x_{\text{A}}} = 2.87\) A1
\({x_{{\text{B}}}} = 6.78\) A1
[2 marks]
\(\int_{2.87172{\text{K}}}^{6.77681K} {1 - 2\sin x - {x^2}{{\text{e}}^{ - x}}{\text{d}}x} \) (M1)(A1)
\( = 6.76\) A1
Note: Award (M1) for definite integral and (A1) for a correct definite integral.
[3 marks]
Examiners report
(a) Find the solution of the equation
\[\ln {2^{4x - 1}} = \ln {8^{x + 5}} + {\log _2}{16^{1 - 2x}},\]
expressing your answer in terms of \(\ln 2\).
(b) Using this value of x, find the value of a for which \({\log _a}x = 2\), giving your answer to three decimal places.
Markscheme
(a) rewrite the equation as \((4x - 1)\ln 2 = (x + 5)\ln 8 + (1 - 2x){\log _2}16\) (M1)
\((4x - 1)\ln 2 = (3x + 15)\ln 2 + 4 - 8x\) (M1)(A1)
\(x = \frac{{4 + 16\ln 2}}{{8 + \ln 2}}\) A1
(b) \(x = {a^2}\) (M1)
\(a = 1.318\) A1
Note: Treat 1.32 as an AP.
Award A0 for ±.
[6 marks]
Examiners report
A more difficult question. Many candidates failed to read the question carefully so did not express x in terms of \(\ln 2\).
Given that (x − 2) is a factor of \(f(x) = {x^3} + a{x^2} + bx - 4\) and that division \(f(x)\) by (x − 1) leaves a remainder of −6 , find the value of a and the value of b .
Markscheme
\(f(2) = 8 + 4a + 2b - 4 = 0\) M1
\( \Rightarrow 4a + 2b = - 4\) A1
\(f(1) = 1 + a + b - 4 = - 6\) M1
\( \Rightarrow a + b = - 3\) A1
solving, \(a = 1,{\text{ }}b = - 4\) A1A1
[6 marks]
Examiners report
Given that \(f(x) = \frac{1}{{1 + {{\text{e}}^{ - x}}}}\),
find \({f^{ - 1}}(x)\), stating its domain;
find the value of x such that \(f(x) = {f^{ - 1}}(x)\).
Markscheme
\(y = \frac{1}{{1 + {{\text{e}}^{ - x}}}}\)
\(y(1 + {{\text{e}}^{ - x}}) = 1\) M1
\(1 + {{\text{e}}^{ - x}} = \frac{1}{y} \Rightarrow {{\text{e}}^{ - x}} = \frac{1}{y} - 1\) A1
\( \Rightarrow x = - \ln \left( {\frac{1}{y} - 1} \right)\) A1
\({f^{ - 1}}(x) = - \ln \left( {\frac{1}{x} - 1} \right)\,\,\,\,\,\left( { = \ln \left( {\frac{x}{{1 - x}}} \right)} \right)\) A1
domain: 0 < x < 1 A1A1
Note: Award A1 for endpoints and A1 for strict inequalities.
[6 marks]
0.659 A1
[1 mark]
Examiners report
Finding the inverse function was done successfully by a very large number of candidates. The domain, however, was not always correct. Some candidates failed to use the GDC correctly to find (b), while other candidates had unsuccessful attempts at an analytic solution.
Finding the inverse function was done successfully by a very large number of candidates. The domain, however, was not always correct. Some candidates failed to use the GDC correctly to find (b), while other candidates had unsuccessful attempts at an analytic solution.
The sum of the first 16 terms of an arithmetic sequence is 212 and the fifth term is 8.
Find the first term and the common difference.
Find the smallest value of n such that the sum of the first n terms is greater than 600.
Markscheme
\({S_n} = \frac{n}{2}[2a + (n - 1)d]\)
\(212 = \frac{{16}}{2}(2a + 15d)\,\,\,\,\,( = 16a + 120d)\) A1
\({n^{th}}{\text{ term is }}a + (n - 1)d\)
\(8 = a + 4d\) A1
solving simultaneously: (M1)
\(d = 1.5,{\text{ }}a = 2\) A1
[4 marks]
\(\frac{n}{2}[4 + 1.5(n - 1)] > 600\) (M1)
\( \Rightarrow 3{n^2} + 5n - 2400 > 0\) (A1)
\( \Rightarrow n > 27.4...,{\text{ }}(n < - 29.1...)\)
Note: Do not penalize improper use of inequalities.
\( \Rightarrow n = 28\) A1
[3 marks]
Examiners report
This proved to be a good start to the paper for most candidates. The vast majority made a meaningful attempt at this question with many gaining the correct answers. Candidates who lost marks usually did so because of mistakes in the working. In part (b) the most efficient way of gaining the answer was to use the calculator once the initial inequality was set up. A small number of candidates spent valuable time unnecessarily manipulating the algebra before moving to the calculator.
This proved to be a good start to the paper for most candidates. The vast majority made a meaningful attempt at this question with many gaining the correct answers. Candidates who lost marks usually did so because of mistakes in the working. In part (b) the most efficient way of gaining the answer was to use the calculator once the initial inequality was set up. A small number of candidates spent valuable time unnecessarily manipulating the algebra before moving to the calculator.
The function \(f\) is defined as \(f(x) = \sqrt {\frac{{1 - x}}{{1 + x}}} ,{\text{ }} - 1 < x \leqslant 1\).
Find the inverse function, \({f^{ - 1}}\) stating its domain and range.
Markscheme
\(x = \sqrt {\frac{{1 - y}}{{1 + y}}} \) M1
Note: Award M1 for interchanging \(x\) and \(y\) (can be done at a later stage).
\({x^2} = \frac{{1 - y}}{{1 + y}}\)
\({x^2} + {x^2}y = 1 - y\) M1
Note: Award M1 for attempting to make \(y\) the subject.
\(y(1 + {x^2}) = 1 - {x^2}\) (A1)
\({f^{ - 1}}(x) = \frac{{1 - {x^2}}}{{1 + {x^2}}},{\text{ }}x \geqslant 0\) A1A1
Note: Award A1 only if \({f^{ - 1}}(x)\) is seen. Award A1 for the domain.
the range of \({f^{ - 1}}\) is \( - 1 < {f^{ - 1}}(x) \leqslant 1\) A1
Note: Accept correct alternative notation eg. \( - 1 < y \leqslant 1\).
[6 marks]
Examiners report
Most candidates were able to find an expression for the inverse function. A large number of candidates however were unable to determine the domain and range of the inverse.
Compactness is a measure of how compact an enclosed region is.
The compactness, \(C\) , of an enclosed region can be defined by \(C = \frac{{4A}}{{\pi {d^2}}}\), where \(A\) is the area of the region and \(d\) is the maximum distance between any two points in the region.
For a circular region, \(C = 1\).
Consider a regular polygon of \(n\) sides constructed such that its vertices lie on the circumference of a circle of diameter \(x\) units.
If \(n > 2\) and even, show that \(C = \frac{n}{{2\pi }}\sin \frac{{2\pi }}{n}\).
If \(n > 1\) and odd, it can be shown that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\).
Find the regular polygon with the least number of sides for which the compactness is more than \(0.99\).
If \(n > 1\) and odd, it can be shown that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\).
Comment briefly on whether C is a good measure of compactness.
Markscheme
each triangle has area \(\frac{1}{8}{x^2}\sin \frac{{2\pi }}{n}\;\;\;({\text{use of }}\frac{1}{2}ab\sin C)\) (M1)
there are \(n\) triangles so \(A = \frac{1}{8}n{x^2}\sin \frac{{2\pi }}{n}\) A1
\(C = \frac{{4\left( {\frac{1}{8}n{x^2}\sin \frac{{2\pi }}{n}} \right)}}{{\pi {n^2}}}\) A1
so \(C = \frac{n}{{2\pi }}\sin \frac{{2\pi }}{n}\) AG
[3 marks]
attempting to find the least value of \(n\) such that \(\frac{n}{{2\pi }}\sin \frac{{2\pi }}{n} > 0.99\) (M1)
\(n = 26\) A1
attempting to find the least value of \(n\) such that \(\frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}} > 0.99\) (M1)
\(n = 21\) (and so a regular polygon with 21 sides) A1
Note: Award (M0)A0(M1)A1 if \(\frac{n}{{2\pi }}\sin \frac{{2\pi }}{n} > 0.99\) is not considered and \(\frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}} > 0.99\) is correctly considered.
Award (M1)A1(M0)A0 for \(n = 26\).
[4 marks]
EITHER
for even and odd values of n, the value of C seems to increase towards the limiting value of the circle \((C = 1)\) ie as n increases, the polygonal regions get closer and closer to the enclosing circular region R1
OR
the differences between the odd and even values of n illustrate that this measure of compactness is not a good one. R1
Examiners report
Most candidates found this a difficult question with a large number of candidates either not attempting it or making little to no progress. In part (a), a number of candidates attempted to show the desired result using specific regular polygons. Some candidates attempted to fudge the result.
In part (b), the overwhelming majority of candidates that obtained either \(n = 21\) or \(n = 26\) or both used either a GDC numerical solve feature or a graphical approach rather than a tabular approach which is more appropriate for a discrete variable such as the number of sides of a regular polygon. Some candidates wasted valuable time by showing that \(C = \frac{{n\sin \frac{{2\pi }}{n}}}{{\pi \left( {1 + \cos \frac{\pi }{n}} \right)}}\) (a given result).
In part (c), the occasional candidate correctly commented that \(C \) was a good measure of compactness either because the value of \(C \) seemed to approach the limiting value of the circle as \(n \) increased or commented that \(C \) was not a good measure because of the disparity in \(C \)-values between even and odd values of \(n \).
The diagram below shows a semi-circle of diameter 20 cm, centre O and two points A and B such that \({\rm{A\hat OB}} = \theta \), where \(\theta \) is in radians.

Show that the shaded area can be expressed as \(50\theta - 50\sin \theta \).
Find the value of \(\theta \) for which the shaded area is equal to half that of the unshaded area, giving your answer correct to four significant figures.
Markscheme
\(A = \frac{1}{2} \times {10^2} \times \theta - \frac{1}{2} \times {10^2} \times \sin \theta \) M1A1
Note: Award M1 for use of area of segment = area of sector – area of triangle.
\( = 50\theta - 50\sin \theta \) AG
[2 marks]
METHOD 1
unshaded area \( = \frac{{\pi \times {{10}^2}}}{2} - 50(\theta - \sin \theta )\)
(or equivalent eg \(50\pi - 50\theta + 50\sin \theta )\) (M1)
\(50\theta - 50\sin \theta = \frac{1}{2}(50\pi - 50\theta + 50\sin \theta )\) (A1)
\(3\theta - 3\sin \theta - \pi = 0\)
\( \Rightarrow \theta = 1.969{\text{ (rad)}}\) A1
METHOD 2
\(50\theta - 50\sin \theta = \frac{1}{3}\left( {\frac{{\pi \times {{10}^2}}}{2}} \right)\) (M1)(A1)
\(3\theta - 3\sin \theta - \pi = 0\)
\( \Rightarrow \theta = 1.969{\text{ (rad)}}\) A1
[3 marks]
Examiners report
Part (a) was very well done. Most candidates knew how to calculate the area of a segment. A few candidates used \(r = 20\).
Part (b) challenged a large proportion of candidates. A common error was to equate the unshaded area and the shaded area. Some candidates expressed their final answer correct to three significant figures rather than to the four significant figures specified.
Let \(f(x) = \ln x\) . The graph of f is transformed into the graph of the function g by a translation of \(\left( {\begin{array}{*{20}{c}}
3 \\
{ - 2}
\end{array}} \right)\), followed by a reflection in the x-axis. Find an expression for \(g(x)\), giving your answer as a single logarithm.
Markscheme
\(h(x) = f(x - 3) - 2 = \ln (x - 3) - 2\) (M1)(A1)
\(g(x) = -h(x) = 2 - \ln (x - 3)\) M1
Note: Award M1 only if it is clear the effect of the reflection in the x-axis:
the expression is correct OR
there is a change of signs of the previous expression OR
there’s a graph or an explanation making it explicit
\( = \ln {{\text{e}}^2} - \ln (x - 3)\) M1
\( = \ln \left( {\frac{{{{\text{e}}^2}}}{{x - 3}}} \right)\) A1
[5 marks]
Examiners report
This question was well attempted but many candidates could have scored better had they written down all the steps to obtain the final expression. In some cases, as the final expression was incorrect and the middle steps were missing, candidates scored just 1 mark. That could be a consequence of a small mistake, but the lack of working prevented them from scoring at least all method marks. Some candidates performed the transformations well but were not able to use logarithms properties to transform the answer and give it as a single logarithm.
Find the acute angle between the planes with equations \(x + y + z = 3\) and \(2x - z = 2\).
Markscheme
n\(_1 = \left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 1 \end{array}} \right)\) and n\(_2 = \left( {\begin{array}{*{20}{c}} 2 \\ 0 \\ { - 1} \end{array}} \right)\) (A1)(A1)
EITHER
\(\theta = \arccos \left( {\frac{{{n_1} \bullet {n_2}}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)\left( {\cos \theta = \frac{{{n_1} \bullet {n_2}}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)\) (M1)
\( = \arccos \left( {\frac{{2 + 0 - 1}}{{\sqrt 3 \sqrt 5 }}} \right)\left( {\cos \theta = \frac{{2 + 0 - 1}}{{\sqrt 3 \sqrt 5 }}} \right)\) (A1)
\( = \arccos \left( {\frac{1}{{\sqrt {15} }}} \right)\left( {\cos \theta = \frac{1}{{\sqrt {15} }}} \right)\)
OR
\(\theta = \arcsin \left( {\frac{{\left| {{n_1} \times {n_2}} \right|}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)\left( {\sin \theta = \frac{{\left| {{n_1} \times {n_2}} \right|}}{{\left| {{n_1}} \right|\left| {{n_2}} \right|}}} \right)\) (M1)
\( = \arcsin \left( {\frac{{\sqrt {14} }}{{\sqrt 3 \sqrt 5 }}} \right)\left( {\sin \theta = \frac{{\sqrt {14} }}{{\sqrt 3 \sqrt 5 }}} \right)\) (A1)
\( = \arcsin \left( {\frac{{\sqrt {14} }}{{\sqrt {15} }}} \right)\left( {\sin \theta = \frac{{\sqrt {14} }}{{\sqrt {15} }}} \right)\)
THEN
\( = 75.0^\circ {\text{ (or 1.31)}}\) A1
[5 marks]
Examiners report
Let \(f(x) = \frac{{{{\text{e}}^{2x}} + 1}}{{{{\text{e}}^x} - 2}}\).
The line \({L_2}\) is parallel to \({L_1}\) and tangent to the curve \(y = f(x)\).
Find the equations of the horizontal and vertical asymptotes of the curve \(y = f(x)\).
(i) Find \(f'(x)\).
(ii) Show that the curve has exactly one point where its tangent is horizontal.
(iii) Find the coordinates of this point.
Find the equation of \({L_1}\), the normal to the curve at the point where it crosses the y-axis.
Find the equation of the line \({L_2}\).
Markscheme
\(x \to - \infty \Rightarrow y \to - \frac{1}{2}\) so \(y = - \frac{1}{2}\) is an asymptote (M1)A1
\({{\text{e}}^x} - 2 = 0 \Rightarrow x = \ln 2\) so \(x = \ln 2{\text{ }}( = 0.693)\) is an asymptote (M1)A1
[4 marks]
(i) \(f'(x) = \frac{{2\left( {{{\text{e}}^x} - 2} \right){{\text{e}}^{2x}} - \left( {{{\text{e}}^{2x}} + 1} \right){{\text{e}}^x}}}{{{{\left( {{{\text{e}}^x} - 2} \right)}^2}}}\) M1A1
\( = \frac{{{{\text{e}}^{3x}} - 4{{\text{e}}^{2x}} - {{\text{e}}^x}}}{{{{\left( {{{\text{e}}^x} - 2} \right)}^2}}}\)
(ii) \(f'(x) = 0\) when \({{\text{e}}^{3x}} - 4{{\text{e}}^{2x}} - {{\text{e}}^x} = 0\) M1
\({{\text{e}}^x}\left( {{{\text{e}}^{2x}} - 4{{\text{e}}^x} - 1} \right) = 0\)
\({{\text{e}}^x} = 0,{\text{ }}{{\text{e}}^x} = - 0.236,{\text{ }}{{\text{e}}^x} = 4.24{\text{ }}({\text{or }}{{\text{e}}^x} = 2 \pm \sqrt 5 )\) A1A1
Note: Award A1 for zero, A1 for other two solutions.
Accept any answers which show a zero, a negative and a positive.
as \({{\text{e}}^x} > 0\) exactly one solution R1
Note: Do not award marks for purely graphical solution.
(iii) (1.44, 8.47) A1A1
[8 marks]
\(f'(0) = - 4\) (A1)
so gradient of normal is \(\frac{1}{4}\) (M1)
\(f(0) = - 2\) (A1)
so equation of \({L_1}\) is \(y = \frac{1}{4}x - 2\) A1
[4 marks]
\(f'(x) = \frac{1}{4}\) M1
so \(x = 1.46\) (M1)A1
\(f(1.46) = 8.47\) (A1)
equation of \({L_2}\) is \(y - 8.47 = \frac{1}{4}(x - 1.46)\) A1
(or \(y = \frac{1}{4}x + 8.11\))
[5 marks]
Examiners report
Sketch the curve \(y = \frac{{\cos x}}{{\sqrt {{x^2} + 1} }},{\text{ }} - 4 \leqslant x \leqslant 4\) showing clearly the coordinates of the x-intercepts, any maximum points and any minimum points.
Write down the gradient of the curve at x = 1 .
Find the equation of the normal to the curve at x = 1 .
Markscheme
A1A1A1A1
Note: Award A1 for correct shape. Do not penalise if too large a domain is used,
A1 for correct x-intercepts,
A1 for correct coordinates of two minimum points,
A1 for correct coordinates of maximum point.
Accept answers which correctly indicate the position of the intercepts, maximum point and minimum points.
[4 marks]
gradient at x = 1 is –0.786 A1
[1 mark]
gradient of normal is \(\frac{{ - 1}}{{ - 0.786}}( = 1.272...)\) (A1)
when x = 1, y = 0.3820... (A1)
Equation of normal is y – 0.382 = 1.27(x – 1) A1
\(( \Rightarrow y = 1.27x - 0.890)\)
[3 marks]
Examiners report
Most candidates were able to make a meaningful start to this question, but many made errors along the way and hence only a relatively small number of candidates gained full marks for the question. Common errors included trying to use degrees, rather than radians, trying to use algebraic methods to find the gradient in part (b) and trying to find the equation of the tangent rather than the equation of the normal in part (c).
Most candidates were able to make a meaningful start to this question, but many made errors along the way and hence only a relatively small number of candidates gained full marks for the question. Common errors included trying to use degrees, rather than radians, trying to use algebraic methods to find the gradient in part (b) and trying to find the equation of the tangent rather than the equation of the normal in part (c).
Most candidates were able to make a meaningful start to this question, but many made errors along the way and hence only a relatively small number of candidates gained full marks for the question. Common errors included trying to use degrees, rather than radians, trying to use algebraic methods to find the gradient in part (b) and trying to find the equation of the tangent rather than the equation of the normal in part (c).
The diagram shows the graphs of a linear function f and a quadratic function g.
On the same axes sketch the graph of \(\frac{f}{g}\). Indicate clearly where the x-intercept and the asymptotes occur.
Markscheme
correct concavities A1A1
Note: Award A1 for concavity of each branch of the curve.
correct x-intercept of \(\frac{f}{g}\) (which is EXACTLY the x-intercept of f) A1
correct vertical asymptotes of \(\frac{f}{g}\) (which ONLY occur when x equals the x-intercepts of g) A1A1
[5 marks]
Examiners report
Many candidates answered well this question. Full marks were often achieved. Many other candidates did not attempt it at all.
(i) Express the sum of the first n positive odd integers using sigma notation.
(ii) Show that the sum stated above is \({n^2}\).
(iii) Deduce the value of the difference between the sum of the first 47 positive odd integers and the sum of the first 14 positive odd integers.
A number of distinct points are marked on the circumference of a circle, forming a polygon. Diagonals are drawn by joining all pairs of non-adjacent points.
(i) Show on a diagram all diagonals if there are 5 points.
(ii) Show that the number of diagonals is \(\frac{{n(n - 3)}}{2}\) if there are n points, where \(n > 2\).
(iii) Given that there are more than one million diagonals, determine the least number of points for which this is possible.
The random variable \(X \sim B(n,{\text{ }}p)\) has mean 4 and variance 3.
(i) Determine n and p.
(ii) Find the probability that in a single experiment the outcome is 1 or 3.
Markscheme
(i) \(\sum\limits_{k = 1}^n {(2k - 1)} \) (or equivalent) A1
Note: Award A0 for \(\sum\limits_{n = 1}^n {(2n - 1)} \) or equivalent.
(ii) EITHER
\(2 \times \frac{{n(n + 1)}}{2} - n\) M1A1
OR
\(\frac{n}{2}\left( {2 + (n - 1)2} \right){\text{ (using }}{S_n} = \frac{n}{2}\left( {2{u_1} + (n - 1)d} \right))\) M1A1
OR
\(\frac{n}{2}(1 + 2n - 1){\text{ (using }}{S_n} = \frac{n}{2}({u_1} + {u_n}))\) M1A1
THEN
\( = {n^2}\) AG
(iii) \({47^2} - {14^2} = 2013\) A1
[4 marks]
(i) EITHER
a pentagon and five diagonals A1
OR
five diagonals (circle optional) A1
(ii) Each point joins to n – 3 other points. A1
a correct argument for \({n(n - 3)}\) R1
a correct argument for \(\frac{{n(n - 3)}}{2}\) R1
(iii) attempting to solve \(\frac{1}{2}n(n - 3) > 1\,000\,000\) for n. (M1)
\(n > 1415.7\) (A1)
\(n = 1416\) A1
[7 marks]
(i) np = 4 and npq = 3 (A1)
attempting to solve for n and p (M1)
\(n = 16\) and \(p = \frac{1}{4}\) A1
(ii) \(X \sim B(16,0.25)\) (A1)
\(P(X = 1) = 0.0534538...( = \left( {\begin{array}{*{20}{c}}
{16} \\
1
\end{array}} \right)(0.25){(0.75)^{15}})\) (A1)
\(P(X = 3) = 0.207876...( = \left( {\begin{array}{*{20}{c}}
{16} \\
3
\end{array}} \right){(0.25)^3}{(0.75)^{13}})\) (A1)
\({\text{P}}(X = 1) + {\text{P}}(X = 3)\) (M1)
= 0.261 A1
[8 marks]
Examiners report
In part (a) (i), a large number of candidates were unable to correctly use sigma notation to express the sum of the first n positive odd integers. Common errors included summing \(2n - 1\) from 1 to n and specifying sums with incorrect limits. Parts (a) (ii) and (iii) were generally well done.
Parts (b) (i) and (iii) were generally well done. In part (b) (iii), many candidates unnecessarily simplified their quadratic when direct GDC use could have been employed. A few candidates gave \(n > 1416\) as their final answer. While some candidates displayed sound reasoning in part (b) (ii), many candidates unfortunately adopted a ‘proof by example’ approach.
Part (c) was generally well done. In part (c) (ii), some candidates multiplied the two probabilities rather than adding the two probabilities.
A straight street of width 20 metres is bounded on its parallel sides by two vertical walls, one of height 13 metres, the other of height 8 metres. The intensity of light at point P at ground level on the street is proportional to the angle \(\theta \) where \(\theta = {\rm{A\hat PB}}\), as shown in the diagram.
Find an expression for \(\theta \) in terms of x, where x is the distance of P from the base of the wall of height 8 m.
(i) Calculate the value of \(\theta \) when x = 0.
(ii) Calculate the value of \(\theta \) when x = 20.
Sketch the graph of \(\theta \), for \(0 \leqslant x \leqslant 20\).
Show that \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = \frac{{5(744 - 64x - {x^2})}}{{({x^2} + 64)({x^2} - 40x + 569)}}\).
Using the result in part (d), or otherwise, determine the value of x corresponding to the maximum light intensity at P. Give your answer to four significant figures.
The point P moves across the street with speed \(0.5{\text{ m}}{{\text{s}}^{ - 1}}\). Determine the rate of change of \(\theta \) with respect to time when P is at the midpoint of the street.
Markscheme
EITHER
\(\theta = \pi - \arctan \left( {\frac{8}{x}} \right) - \arctan \left( {\frac{{13}}{{20 - x}}} \right)\) (or equivalent) M1A1
Note: Accept \(\theta = 180^\circ - \arctan \left( {\frac{8}{x}} \right) - \arctan \left( {\frac{{13}}{{20 - x}}} \right)\) (or equivalent).
OR
\(\theta = \arctan \left( {\frac{x}{8}} \right) + \arctan \left( {\frac{{20 - x}}{{13}}} \right)\) (or equivalent) M1A1
[2 marks]
(i) \(\theta = 0.994{\text{ }}\left( { = \arctan \frac{{20}}{{13}}} \right)\) A1
(ii) \(\theta = 1.19{\text{ }}\left( { = \arctan \frac{5}{2}} \right)\) A1
[2 marks]
correct shape. A1
correct domain indicated. A1
[2 marks]
attempting to differentiate one \(\arctan \left( {f(x)} \right)\) term M1
EITHER
\(\theta = \pi - \arctan \left( {\frac{8}{x}} \right) - \arctan \left( {\frac{{13}}{{20 - x}}} \right)\)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = \frac{8}{{{x^2}}} \times \frac{1}{{1 + {{\left( {\frac{8}{x}} \right)}^2}}} - \frac{{13}}{{{{(20 - x)}^2}}} \times \frac{1}{{1 + {{\left( {\frac{{13}}{{20 - x}}} \right)}^2}}}\) A1A1
OR
\(\theta = \arctan \left( {\frac{x}{8}} \right) + \arctan \left( {\frac{{20 - x}}{{13}}} \right)\)
\(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = \frac{{\frac{1}{8}}}{{1 + {{\left( {\frac{x}{8}} \right)}^2}}} + \frac{{ - \frac{1}{{13}}}}{{1 + {{\left( {\frac{{20 - x}}{{13}}} \right)}^2}}}\) A1A1
THEN
\( = \frac{8}{{{x^2} + 64}} - \frac{{13}}{{569 - 40x + {x^2}}}\) A1
\( = \frac{{8(569 - 40x + {x^2}) - 13({x^{2}} + 64)}}{{({x^2} + 64)({x^2} - 40x + 569)}}\) M1A1
\( = \frac{{5(744 - 64x - {x^2})}}{{({x^2} + 64)({x^2} - 40x + 569)}}\) AG
[6 marks]
Maximum light intensity at P occurs when \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = 0\). (M1)
either attempting to solve \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = 0\) for x or using the graph of either \(\theta \) or \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}}\) (M1)
x = 10.05 (m) A1
[3 marks]
\(\frac{{{\text{d}}x}}{{{\text{d}}t}} = 0.5\) (A1)
At x = 10, \(\frac{{{\text{d}}\theta }}{{{\text{d}}x}} = 0.000453{\text{ }}\left( { = \frac{5}{{11029}}} \right)\). (A1)
use of \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = \frac{{{\text{d}}\theta }}{{{\text{d}}x}} \times \frac{{{\text{d}}x}}{{{\text{d}}t}}\) M1
\(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = 0.000227{\text{ }}\left( { = \frac{5}{{22058}}} \right){\text{ (rad }}{{\text{s}}^{ - 1}})\) A1
Note: Award (A1) for \(\frac{{{\text{d}}x}}{{{\text{d}}t}} = - 0.5\) and A1 for \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}} = - 0.000227{\text{ }}\left( { = - \frac{5}{{22058}}} \right){\text{ }}\).
Note: Implicit differentiation can be used to find \(\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\). Award as above.
[4 marks]
Examiners report
Part (a) was reasonably well done. While many candidates exhibited sound trigonometric knowledge to correctly express θ in terms of x, many other candidates were not able to use elementary trigonometry to formulate the required expression for θ.
In part (b), a large number of candidates did not realize that θ could only be acute and gave obtuse angle values for θ. Many candidates also demonstrated a lack of insight when substituting endpoint x-values into θ.
In part (c), many candidates sketched either inaccurate or implausible graphs.
In part (d), a large number of candidates started their differentiation incorrectly by failing to use the chain rule correctly.
For a question part situated at the end of the paper, part (e) was reasonably well done. A large number of candidates demonstrated a sound knowledge of finding where the maximum value of θ occurred and rejected solutions that were not physically feasible.
In part (f), many candidates were able to link the required rates, however only a few candidates were able to successfully apply the chain rule in a related rates context.
A particle, A, is moving along a straight line. The velocity, \({v_A}{\text{ m}}{{\text{s}}^{ - 1}}\), of A t seconds after its motion begins is given by
\[{v_A} = {t^3} - 5{t^2} + 6t.\]
Sketch the graph of \({v_A} = {t^3} - 5{t^2} + 6t\) for \(t \geqslant 0\), with \({v_A}\) on the vertical axis and t on the horizontal. Show on your sketch the local maximum and minimum points, and the intercepts with the t-axis.
Write down the times for which the velocity of the particle is increasing.
Write down the times for which the magnitude of the velocity of the particle is increasing.
At t = 0 the particle is at point O on the line.
Find an expression for the particle’s displacement, \({x_A}{\text{m}}\), from O at time t.
A second particle, B, moving along the same line, has position \({x_B}{\text{ m}}\), velocity \({v_B}{\text{ m}}{{\text{s}}^{ - 1}}\) and acceleration, \({a_B}{\text{ m}}{{\text{s}}^{ - 2}}\), where \({a_B} = - 2{v_B}\) for \(t \geqslant 0\). At \(t = 0,{\text{ }}{x_B} = 20\) and \({v_B} = - 20\).
Find an expression for \({v_B}\) in terms of t.
Find the value of t when the two particles meet.
Markscheme
A1A1A1
Note: Award A1 for general shape, A1 for correct maximum and minimum, A1 for intercepts.
Note: Follow through applies to (b) and (c).
[3 marks]
\(0 \leqslant t < 0.785,{\text{ }}\left( {{\text{or }}0 \leqslant t < \frac{{5 - \sqrt 7 }}{3}} \right)\) A1
(allow \(t < 0.785\))
and \(t > 2.55{\text{ }}\left( {{\text{or }}t > \frac{{5 + \sqrt 7 }}{3}} \right)\) A1
[2 marks]
\(0 \leqslant t < 0.785,{\text{ }}\left( {{\text{or }}0 \leqslant t < \frac{{5 - \sqrt 7 }}{3}} \right)\) A1
(allow \(t < 0.785\))
\(2 < t < 2.55,{\text{ }}\left( {{\text{or }}2 < t < \frac{{5 + \sqrt 7 }}{3}} \right)\) A1
\(t > 3\) A1
[3 marks]
position of A: \({x_A} = \int {{t^3} - 5{t^2} + 6t{\text{ d}}t} \) (M1)
\({x_A} = \frac{1}{4}{t^4} - \frac{5}{3}{t^3} + 3{t^2}\,\,\,\,\,( + c)\) A1
when \(t = 0,{\text{ }}{x_A} = 0\), so \(c = 0\) R1
[3 marks]
\(\frac{{{\text{d}}{v_B}}}{{{\text{d}}t}} = - 2{v_B} \Rightarrow \int {\frac{1}{{{v_B}}}{\text{d}}{v_B} = \int { - 2{\text{d}}t} } \) (M1)
\(\ln \left| {{v_B}} \right| = - 2t + c\) (A1)
\({v_B} = A{e^{ - 2t}}\) (M1)
\({v_B} = - 20\) when t = 0 so \({v_B} = - 20{e^{ - 2t}}\) A1
[4 marks]
\({x_B} = 10{e^{ - 2t}}( + c)\) (M1)(A1)
\({x_B} = 20{\text{ when }}t = 0{\text{ so }}{x_B} = 10{e^{ - 2t}} + 10\) (M1)A1
meet when \(\frac{1}{4}{t^4} - \frac{5}{3}{t^3} + 3{t^2} = 10{e^{ - 2t}} + 10\) (M1)
\(t = 4.41(290 \ldots )\) A1
[6 marks]
Examiners report
Part (a) was generally well done, although correct accuracy was often a problem.
Parts (b) and (c) were also generally quite well done.
Parts (b) and (c) were also generally quite well done.
A variety of approaches were seen in part (d) and many candidates were able to obtain at least 2 out of 3. A number missed to consider the \(+c\) , thereby losing the last mark.
Surprisingly few candidates were able to solve part (e) correctly. Very few could recognise the easy variable separable differential equation. As a consequence part (f) was frequently left.
Surprisingly few candidates were able to solve part (e) correctly. Very few could recognise the easy variable separable differential equation. As a consequence part (f) was frequently left.
Consider the expression \(f\left( x \right) = {\text{tan}}\left( {x + \frac{\pi }{4}} \right){\text{cot}}\left( {\frac{\pi }{4} - x} \right)\).
The expression \(f\left( x \right)\) can be written as \(g\left( t \right)\) where \(t = {\text{tan}}\,x\).
Let \(\alpha \), β be the roots of \(g\left( t \right) = k\), where 0 < \(k\) < 1.
Sketch the graph of \(y = f\left( x \right)\) for \( - \frac{{5\pi }}{8} \leqslant x \leqslant \frac{\pi }{8}\).
With reference to your graph, explain why \(f\) is a function on the given domain.
Explain why \(f\) has no inverse on the given domain.
Explain why \(f\) is not a function for \( - \frac{{3\pi }}{4} \leqslant x \leqslant \frac{\pi }{4}\).
Show that \(g\left( t \right) = {\left( {\frac{{1 + t}}{{1 - t}}} \right)^2}\).
Sketch the graph of \(y = g\left( t \right)\) for t ≤ 0. Give the coordinates of any intercepts and the equations of any asymptotes.
Find \(\alpha \) and β in terms of \(k\).
Show that \(\alpha \) + β < −2.
Markscheme
A1A1
A1 for correct concavity, many to one graph, symmetrical about the midpoint of the domain and with two axes intercepts.
Note: Axes intercepts and scales not required.
A1 for correct domain
[2 marks]
for each value of \(x\) there is a unique value of \(f\left( x \right)\) A1
Note: Accept “passes the vertical line test” or equivalent.
[1 mark]
no inverse because the function fails the horizontal line test or equivalent R1
Note: No FT if the graph is in degrees (one-to-one).
[1 mark]
the expression is not valid at either of \(x = \frac{\pi }{4}\,\,\left( {{\text{or}} - \frac{{3\pi }}{4}} \right)\) R1
[1 mark]
METHOD 1
\(f\left( x \right) = \frac{{{\text{tan}}\left( {x + \frac{\pi }{4}} \right)}}{{{\text{tan}}\left( {\frac{\pi }{4} - x} \right)}}\) M1
\( = \frac{{\frac{{{\text{tan}}\,x + {\text{tan}}\,\frac{\pi }{4}}}{{1 - {\text{tan}}\,x\,{\text{tan}}\,\frac{\pi }{4}}}}}{{\frac{{{\text{tan}}\,\frac{\pi }{4} - {\text{tan}}\,x}}{{1 + {\text{tan}}\,\frac{\pi }{4}{\text{tan}}\,x}}}}\) M1A1
\( = {\left( {\frac{{1 + t}}{{1 - t}}} \right)^2}\) AG
METHOD 2
\(f\left( x \right) = {\text{tan}}\left( {x + \frac{\pi }{4}} \right){\text{tan}}\left( {\frac{\pi }{2} - \frac{\pi }{4} + x} \right)\) (M1)
\( = {\text{ta}}{{\text{n}}^2}\left( {x + \frac{\pi }{4}} \right)\) A1
\(g\left( t \right) = {\left( {\frac{{{\text{tan}}\,x + {\text{tan}}\,\frac{\pi }{4}}}{{1 - {\text{tan}}\,x\,{\text{tan}}\,\frac{\pi }{4}}}} \right)^2}\) A1
\( = {\left( {\frac{{1 + t}}{{1 - t}}} \right)^2}\) AG
[3 marks]
for t ≤ 0, correct concavity with two axes intercepts and with asymptote \(y\) = 1 A1
t intercept at (−1, 0) A1
\(y\) intercept at (0, 1) A1
[3 marks]
METHOD 1
\(\alpha \), β satisfy \(\frac{{{{\left( {1 + t} \right)}^2}}}{{{{\left( {1 - t} \right)}^2}}} = k\) M1
\(1 + {t^2} + 2t = k\left( {1 + {t^2} - 2t} \right)\) A1
\(\left( {k - 1} \right){t^2} - 2\left( {k + 1} \right)t + \left( {k - 1} \right) = 0\) A1
attempt at using quadratic formula M1
\(\alpha \), β \( = \frac{{k + 1 \pm 2\sqrt k }}{{k - 1}}\) or equivalent A1
METHOD 2
\(\alpha \), β satisfy \(\frac{{1 + t}}{{1 - t}} = \left( \pm \right)\sqrt k \) M1
\(t + \sqrt k t = \sqrt k - 1\) M1
\(t = \frac{{\sqrt k - 1}}{{\sqrt k + 1}}\) (or equivalent) A1
\(t - \sqrt k t = - \left( {\sqrt k + 1} \right)\) M1
\(t = \frac{{\sqrt k + 1}}{{\sqrt k - 1}}\) (or equivalent) A1
so for eg, \(\alpha = \frac{{\sqrt k - 1}}{{\sqrt k + 1}}\), β \( = \frac{{\sqrt k + 1}}{{\sqrt k - 1}}\)
[5 marks]
\(\alpha \) + β \( = 2\frac{{\left( {k + 1} \right)}}{{\left( {k - 1} \right)}}\,\left( { = - 2\frac{{\left( {1 + k} \right)}}{{\left( {1 - k} \right)}}} \right)\) A1
since \(1 + k > 1 - k\) R1
\(\alpha \) + β < −2 AG
Note: Accept a valid graphical reasoning.
[2 marks]
Examiners report
Consider the graph of \(y = x + \sin (x - 3),{\text{ }} - \pi \leqslant x \leqslant \pi \).
Sketch the graph, clearly labelling the x and y intercepts with their values.
Find the area of the region bounded by the graph and the x and y axes.
Markscheme
A1A1A1
Note: Award A1 for shape,
A1 for x-intercept is 0.820, accept \(\sin ( - 3){\text{ or }} - \sin (3)\)
A1 for y-intercept is −0.141.
[3 marks]
\(A = \int_0^{0.8202} {\left| {x + \sin (x - 3)} \right|{\text{d}}x \approx 0.0816{\text{ sq units}}} \) (M1)A1
[2 marks]
Examiners report
Many candidates attempted this question successfully. In (a), however, a large number of candidates did not use the zoom feature of the GDC to draw an accurate sketch of the given function. In (b), some candidates used the domain as the limits of the integral. Other candidates did not take the absolute value of the integral.
Many candidates attempted this question successfully. In (a), however, a large number of candidates did not use the zoom feature of the GDC to draw an accurate sketch of the given function. In (b), some candidates used the domain as the limits of the integral. Other candidates did not take the absolute value of the integral.
(a) Sketch the curve \(y = \left| {\ln x} \right| - \left| {\cos x} \right| - 0.1\) , \(0 < x < 4\) showing clearly the coordinates of the points of intersection with the x-axis and the coordinates of any local maxima and minima.
(b) Find the values of x for which \(\left| {\ln x} \right| > \left| {\cos x} \right| + 0.1\), \(0 < x < 4\) .
Markscheme
(a)
A1
Note: Award A1 for shape.
x-intercepts 0.354, 1.36, 2.59, 2.95 A2
Note: Award A1 for three correct, A0 otherwise.
maximum = (1.57, 0.352) = \(\left( {\frac{\pi }{2},0.352} \right)\) A1
minimum = (1, – 0.640) and (2.77, – 0.0129) A1
(b) \(0 < x < 0.354,{\text{ }}1.36 < x < 2.59,{\text{ }}2.95 < x < 4\) A2
Note: Award A1 if two correct regions given.
[7 marks]
Examiners report
Solutions to this question were extremely disappointing with many candidates doing the sketch in degree mode instead of radian mode. The two adjacent intercepts at 2.59 and 2.95 were often missed due to an unsatisfactory window. Some sketches were so small that a magnifying glass was required to read some of the numbers; candidates would be well advised to draw sketches large enough to be easily read.
Let \(f(x) = \frac{{1 - x}}{{1 + x}}\) and \(g(x) = \sqrt {x + 1} \), \(x > - 1\).
Find the set of values of \(x\) for which \(f'(x) \leqslant f(x) \leqslant g(x)\) .
Markscheme
\(f'(x) = \frac{{ - 2}}{{{{\left( {1 + x} \right)}^2}}}\) M1A1
Note: Alternatively, award M1A1 for correct sketch of the derivative.
find at least one point of intersection of graphs (M1)
\(y = f(x)\) and \(y = f'(x)\) for \(x = \sqrt 3 \) or \(1.73\) (A1)
\(y = f(x)\) and \(y = g(x)\) for \(x = 0\) (A1)
forming inequality \(0 \leqslant x \leqslant \sqrt 3 \) (or \(0 \leqslant x \leqslant 1.73\)) A1A1 N4
Note: Award A1 for correct limits and A1 for correct inequalities.
[7 marks]
Examiners report
Most students were able to find the derived function correctly, although attempts to solve the inequality algebraically were often unsuccessful. This was a question where students prepared in good use of GDC were able to easily obtain good marks.
Let \(f(x) = \frac{{4 - {x^2}}}{{4 - \sqrt x }}\).
(a) State the largest possible domain for f.
(b) Solve the inequality \(f(x) \geqslant 1\).
Markscheme
(a) \(x \geqslant 0\) and \(x \ne 16\) A1A1
(b)
graph not to scale
finding crossing points (M1)
e.g. \(4 - {x^2} = 4 - \sqrt x \)
x = 0 or x = 1 (A1)
\(0 \leqslant x \leqslant 1\) or \(x > 16\) A1A1
Note: Award M1A1A1A0 for solving the inequality only for the case \(x < 16\).
[6 marks]
Examiners report
Most students were able to obtain partial marks, but there were very few completely correct answers.
Consider the function \(g\) , where \(g(x) = \frac{{3x}}{{5 + {x^2}}}\) .
(a) Given that the domain of \(g\) is \(x \geqslant a\) , find the least value of \(a\) such that \(g\) has an inverse function.
(b) On the same set of axes, sketch
(i) the graph of \(g\) for this value of \(a\) ;
(ii) the corresponding inverse, \({g^{ - 1}}\) .
(c) Find an expression for \({g^{ - 1}}(x)\) .
Markscheme
(a) \(a = 2.24\) \(\sqrt 5 \) A1
(b) (i)
A2
Note: Award A1 for end point
A1 for its asymptote.
(ii) sketch of \({g^{ - 1}}\) (see above) A2
Note: Award A1 for end point
A1 for its asymptote.
(c) \(y = \frac{{3x}}{{5 + {x^2}}} \Rightarrow y{x^2} - 3x + 5y = 0\) M1
\( \Rightarrow x = \frac{{3 \pm \sqrt {9 - 20{y^2}} }}{{2y}}\) A1
\({g^{ - 1}}(x) = \frac{{3 \pm \sqrt {9 - 20{x^2}} }}{{2x}}\) A1
[8 marks]
Examiners report
Very few completely correct answers were given to this question. Many students found a to be \(0\) and many failed to provide adequate sketches. There were very few correct answers to part (c) although many students were able to obtain partial marks.
A particle moves in a straight line with velocity v metres per second. At any time t seconds, \(0 \leqslant t < \frac{{3\pi }}{4}\), the velocity is given by the differential equation \(\frac{{{\text{d}}v}}{{{\text{d}}t}} + {v^2} + 1 = 0\) .
It is also given that v = 1 when t = 0 .
Find an expression for v in terms of t .
Sketch the graph of v against t , clearly showing the coordinates of any intercepts, and the equations of any asymptotes.
(i) Write down the time T at which the velocity is zero.
(ii) Find the distance travelled in the interval [0, T] .
Find an expression for s , the displacement, in terms of t , given that s = 0 when t = 0 .
Hence, or otherwise, show that \(s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\).
Markscheme
\(\frac{{{\text{d}}v}}{{{\text{d}}t}} = - {v^2} - 1\)
attempt to separate the variables M1
\(\int {\frac{1}{{1 + {v^2}}}{\text{d}}v = \int { - 1{\text{d}}t} } \) A1
\(\arctan v = - t + k\) A1A1
Note: Do not penalize the lack of constant at this stage.
when t = 0, v = 1 M1
\( \Rightarrow k = \arctan 1 = \left( {\frac{\pi }{4}} \right) = (45^\circ )\) A1
\( \Rightarrow v = \tan \left( {\frac{\pi }{4} - t} \right)\) A1
[7 marks]
A1A1A1
Note: Award A1 for general shape,
A1 for asymptote,
A1 for correct t and v intercept.
Note: Do not penalise if a larger domain is used.
[3 marks]
(i) \(T = \frac{\pi }{4}\) A1
(ii) area under curve \( = \int_0^{\frac{\pi }{4}} {\tan \left( {\frac{\pi }{4} - t} \right){\text{d}}t} \) (M1)
\( = 0.347\left( { = \frac{1}{2}\ln 2} \right)\) A1
[3 marks]
\(v = \tan \left( {\frac{\pi }{4} - t} \right)\)
\(s = \int {\tan \left( {\frac{\pi }{4} - t} \right){\text{d}}t} \) M1
\(\int {\frac{{\sin \left( {\frac{\pi }{4} - t} \right)}}{{\cos \left( {\frac{\pi }{4} - t} \right)}}} {\text{ d}}t\) (M1)
\( = \ln \cos \left( {\frac{\pi }{4} - t} \right) + k\) A1
when \(t = 0,{\text{ }}s = 0\)
\(k = - \ln \cos \frac{\pi }{4}\) A1
\(s = \ln \cos \left( {\frac{\pi }{4} - t} \right) - \ln \cos \frac{\pi }{4}\left( { = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} - t} \right)} \right]} \right)\) A1
[5 marks]
METHOD 1
\(\frac{\pi }{4} - t = \arctan v\) M1
\(t = \frac{\pi }{4} - \arctan v\)
\(s = \ln \left[ {\sqrt 2 \cos \left( {\frac{\pi }{4} - \frac{\pi }{4} + \arctan v} \right)} \right]\)
\(s = \ln \left[ {\sqrt 2 \cos (\arctan v)} \right]\) M1A1
\(s = \ln \left[ {\sqrt 2 \cos \left( {\arccos \frac{1}{{\sqrt {1 + {v^2}} }}} \right)} \right]\) A1
\( = \ln \frac{{\sqrt 2 }}{{\sqrt {1 + {v^2}} }}\)
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 2
\(s = \ln \cos \left( {\frac{\pi }{4} - t} \right) - \ln \cos \frac{\pi }{4}\)
\( = - \ln \sec \left( {\frac{\pi }{4} - t} \right) - \ln \cos \frac{\pi }{4}\) M1
\( = - \ln \sqrt {1 + {{\tan }^2}\left( {\frac{\pi }{4} - t} \right)} - \ln \cos \frac{\pi }{4}\) M1
\( = - \ln \sqrt {1 + {v^2}} - \ln \cos \frac{\pi }{4}\) A1
\( = \ln \frac{1}{{\sqrt {1 + {v^2}} }} + \ln \sqrt 2 \) A1
\( = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
METHOD 3
\(v\frac{{dv}}{{ds}} = - {v^2} - 1\) M1
\(\int {\frac{v}{{{v^2} + 1}}dv = - \int {1ds} } \) M1
\(\frac{1}{2}\ln ({v^2} + 1) = - s + k\) A1
when \(s = 0\,,{\text{ }}t = 0 \Rightarrow v = 1\)
\( \Rightarrow k = \frac{1}{2}\ln 2\) A1
\( \Rightarrow s = \frac{1}{2}\ln \frac{2}{{1 + {v^2}}}\) AG
[4 marks]
Examiners report
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
This proved to be the most challenging question in section B with only a very small number of candidates producing fully correct answers. Many candidates did not realise that part (a) was a differential equation that needed to be solved using a method of separating the variables. Without this, further progress with the question was difficult. For those who did succeed in part (a), parts (b) and (c) were relatively well done. For the minority of candidates who attempted parts (d) and (e) only the best recognised the correct methods.
The function f is defined by
\[f(x) = {({x^3} + 6{x^2} + 3x - 10)^{\frac{1}{2}}},{\text{ for }}x \in D,\]
where \(D \subseteq \mathbb{R}\) is the greatest possible domain of f.
(a) Find the roots of \(f(x) = 0\).
(b) Hence specify the set D.
(c) Find the coordinates of the local maximum on the graph \(y = f(x)\).
(d) Solve the equation \(f(x) = 3\).
(e) Sketch the graph of \(\left| y \right| = f(x),{\text{ for }}x \in D\).
(f) Find the area of the region completely enclosed by the graph of \(\left| y \right| = f(x)\)
Markscheme
(a) solving to obtain one root: 1, – 2 or – 5 A1
obtain other roots A1
[2 marks]
(b) \(D = x \in [ - 5,{\text{ }} - 2] \cup [1,{\text{ }}\infty {\text{)}}\) (or equivalent) M1A1
Note: M1 is for 1 finite and 1 infinite interval.
[2 marks]
(c) coordinates of local maximum \( - 3.73 - 2 - \sqrt 3 ,{\text{ }}3.22\sqrt {6\sqrt 3 } \) A1A1
[2 marks]
(d) use GDC to obtain one root: 1.41, – 3.18 or – 4.23 A1
obtain other roots A1
[2 marks]
(e)
A1A1A1
Note: Award A1 for shape, A1 for max and for min clearly in correct places, A1 for all intercepts.
Award A1A0A0 if only the complete top half is shown.
[3 marks]
(f) required area is twice that of \(y = f(x)\) between – 5 and – 2 M1A1
answer 14.9 A1 N3
Note: Award M1A0A0 for \(\int_{ - 5}^{ - 2} {f(x){\text{d}}x = 7.47 \ldots } \) or N1 for 7.47.
[3 marks]
Total [14 marks]
Examiners report
This was a multi-part question that was well answered by many candidates. The main difficulty was sketching the graph and this meant that the last part was not well answered.
(a) Sketch the curve \(f(x) = \left| {1 + 3\sin (2x)} \right|{\text{, for }}0 \leqslant x \leqslant \pi \) . Write down on the graph the values of the x and y intercepts.
(b) By adding one suitable line to your sketch, find the number of solutions to the equation \(\pi f(x) = 4(\pi - x)\) .
Markscheme
(a)
A1A1A1A1
Note: Award A1 for y-intercept
A1A1 for x-intercepts
A1 for shape
(b) correct line A1
5 solutions A1
[6 marks]
Examiners report
Part (a) was well executed by the majority of candidates. Most candidates had the correct graph with the correct x and y intercepts. For part (b), some candidates had the straight line intersect the x-axis at 3 rather than at \(\pi \) , and hence did not observe that there were 5 points of intersection.
Sketch the graph of \(f(x) = x + \frac{{8x}}{{{x^2} - 9}}\). Clearly mark the coordinates of the two maximum points and the two minimum points. Clearly mark and state the equations of the vertical asymptotes and the oblique asymptote.
Markscheme
M1A1A1A1A1A1A1
Note: Award A1 for both vertical asymptotes correct,
M1 for recognizing that there are two turning points near the origin,
A1 for both turning points near the origin correct, (only this A mark is dependent on the M mark)
A1 for the other pair of turning points correct,
A1 for correct positioning of the oblique asymptote,
A1 for correct equation of the oblique asymptote,
A1 for correct asymptotic behaviour in all sections.
[7 marks]
Examiners report
This question was generally well done, except for the behaviour near the origin. The questions alerted candidates to the existence of four turning points and an oblique asymptote, but not all reported back on this information.
The graph of \(y = f(x){\text{ for }} - 2 \leqslant x \leqslant 8\) is shown.
On the set of axes provided, sketch the graph of \(y = \frac{1}{{f(x)}}\), clearly showing any asymptotes and indicating the coordinates of any local maxima or minima.
Markscheme
A1A1A1A1A1
Notes: Award A1 for vertical asymptotes at x = −1, x = 2 and x = 5 .
A1 for \(x \to - 2,{\text{ }}\frac{1}{{f(x)}} \to {0^ + }\)
A1 for \(x \to 8,{\text{ }}\frac{1}{{f(x)}} \to - 1\)
A1 for local maximum at \(\left( {0, - \frac{1}{2}} \right)\) (branch containing local max. must be present)
A1 for local minimum at (3, 1) (branch containing local min. must be present)
In each branch, correct asymptotic behaviour must be displayed to obtain the A1.
Disregard any stated horizontal asymptotes such as y = 0 or y = −1 .
[5 marks]
Examiners report
A large number of candidates had difficulty graphing the reciprocal function. Most candidates were able to locate the vertical asymptotes but experienced difficulties graphing the four constituent branches. A common error was to specify incorrect coordinates of the local maximum i.e. (0,–1) or (0,–2) instead of \(\left( {0, - \frac{1}{2}} \right)\). A few candidates attempted to sketch the inverse while others had difficulty using the scaled grid.