
SL Paper 3
Data from distant galaxies are shown on the graph.
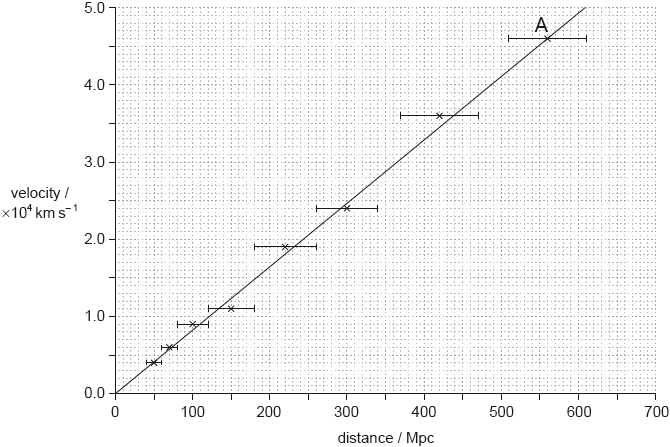
Estimate, using the data, the age of the universe. Give your answer in seconds.
Identify the assumption that you made in your answer to (a).
On the graph, one galaxy is labelled A. Determine the size of the universe, relative to its present size, when light from the galaxy labelled A was emitted.
Markscheme
use of gradient or any coordinate pair to find H0 «= \(\frac{v}{d}\)» or \(\frac{1}{{{H_0}}}\) «= \(\frac{d}{v}\)»
convert Mpc to m and km to m «for example \(\frac{{82 \times {{10}^3}}}{{{{10}^6} \times 3.26 \times 9.46 \times {{10}^{15}}}}\)»
age of universe «= \(\frac{1}{{{H_0}}}\)» = 3.8 × 1017 «s»
Allow final answers between
3.7 × 1017 and 3.9 × 1017 «s» or 4 × 1017 «s»
[3 marks]
non-accelerated/uniform rate of expansion
OR
H0 constant over time
OWTTE
[1 mark]
z « = \(\frac{v}{c}\)» = \(\frac{{4.6 \times {{10}^4} \times {{10}^3}}}{{3.00 \times {{10}^8}}}\) = 0.15
\(\frac{R}{{{R_0}}}\) = «z + 1» = 1.15
\(\frac{{{R_0}}}{R}\) = «\(\frac{1}{{1.15}}\) =» 0.87
OR
87% of the present size
[3 marks]
Examiners report
Distinguish between the solar system and a galaxy.
Distinguish between a planet and a comet.
Markscheme
a galaxy is much larger in size than a solar system
a galaxy contains more than one star system / solar system
a galaxy is more luminous
Any other valid statement.
[1 mark]
a comet is a small icy body whereas a planet is mostly made of rock or gas
a comet is often accompanied by a tail/coma whereas a planet is not
comets (generally) have larger orbits than planets
a planet must have cleared other objects out of the way in its orbital neighbourhood
[1 mark]
Examiners report
Theta 1 Orionis is a main sequence star. The following data for Theta 1 Orionis are available.
| Luminosity | L = 4 × 105 L\(_ \odot \) |
| Radius | R = 13R\(_ \odot \) |
| Apparent brightness | b = 4 × 10–11 b\(_ \odot \) |
where L\(_ \odot \), R\(_ \odot \) and b\(_ \odot \) are the luminosity, radius and apparent brightness of the Sun.
State what is meant by a main sequence star.
Show that the mass of Theta 1 Orionis is about 40 solar masses.
The surface temperature of the Sun is about 6000 K. Estimate the surface temperature of Theta 1 Orionis.
Determine the distance of Theta 1 Orionis in AU.
Discuss how Theta 1 Orionis does not collapse under its own weight.
The Sun and Theta 1 Orionis will eventually leave the main sequence. Compare and contrast the different stages in the evolution of the two stars.
Markscheme
stars fusing hydrogen «into helium»
[1 mark]
\(M = {M_ \odot }{\left( {4 \times {{10}^5}} \right)^{\frac{1}{{3.5}}}} = 39.86{M_ \odot }\)
«\(M \approx 40{M_ \odot }\)»
Accept reverse working.
[1 mark]
\(4 \times {10^5} = {13^2} \times \frac{{{T^4}}}{{{{6000}^4}}}\)
\(T \approx 42\,000\) «K»
Accept use of substituted values into \(L = \sigma \)4\(\pi \)R2T4.
Award [2] for a bald correct answer.
[2 marks]
\(4 \times {10^{ - 11}} = 4 \times {10^5} \times \frac{{1{\text{A}}{{\text{U}}^2}}}{{{d^2}}}\)
\(d = 1 \times {10^8}\) «AU»
Accept use of correct values into \(b = \frac{L}{{4\pi {d^2}}}\).
[2 marks]
the gravitation «pressure» is balanced by radiation «pressure»
that is created by the production of energy due to fusion in the core / OWTTE
Award [1 max] if pressure and force is inappropriately mixed in the answer.
Award [1 max] for unexplained "hydrostatic equilibrium is reached".
[2 marks]
the Sun will evolve to become a red giant whereas Theta 1 Orionis will become a red super giant
the Sun will explode as a planetary nebula whereas Theta 1 Orionis will explode as a supernova
the Sun will end up as a white dwarf whereas Theta 1 Orionis as a neutron star/black hole
[3 marks]
Examiners report
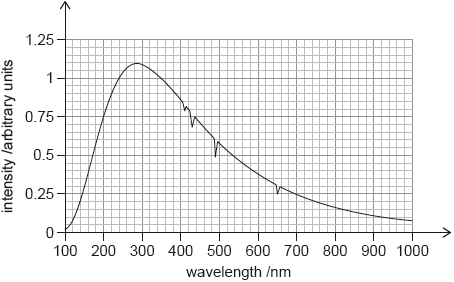
The graph shows the observed spectrum from star X.
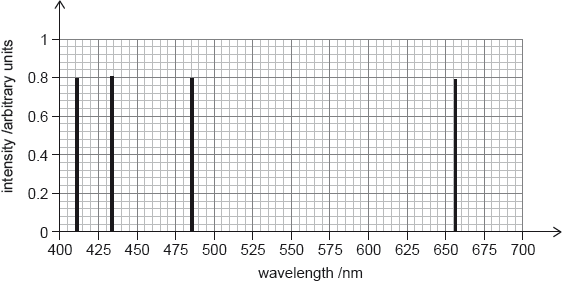
The second graph shows the hydrogen emission spectrum in the visible range.
The following diagram shows the main sequence.
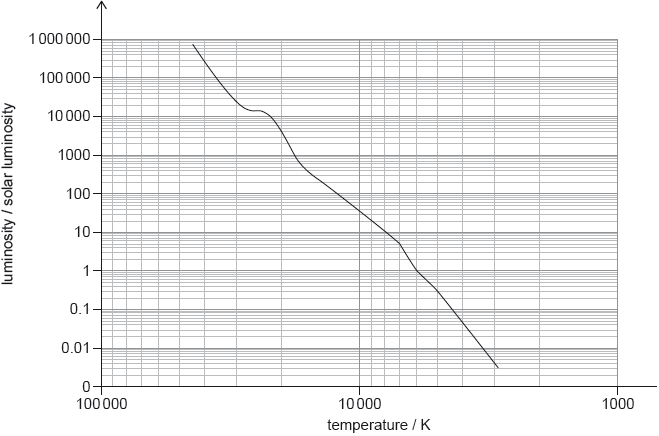
Suggest, using the graphs, why star X is most likely to be a main sequence star.
Show that the temperature of star X is approximately 10 000 K.
Write down the luminosity of star X (LX) in terms of the luminosity of the Sun (Ls).
Determine the radius of star X (RX) in terms of the radius of the Sun (Rs).
Estimate the mass of star X (MX) in terms of the mass of the Sun (Ms).
Star X is likely to evolve into a stable white dwarf star.
Outline why the radius of a white dwarf star reaches a stable value.
Markscheme
the wavelengths of the dips correspond to the wavelength in the emission spectrum
the absorption lines in the spectrum of star X suggest it contains predominantly hydrogen
OR
main sequence stars are rich in hydrogen
[2 marks]
peak wavelength: 290 ± 10 «nm»
T = \(\frac{{2.9 \times {{10}^{-3}}}}{{290 \times {{10}^{ - 9}}}}\) = «10 000 ± 400 K»
Substitution in equation must be seen.
Allow ECF from MP1.
[2 marks][
35 ± 5Ls
[1 mark]
\(\frac{{{L_{\text{X}}}}}{{{L_{\text{s}}}}} = \frac{{R_{\text{X}}^2 \times {\text{T}}_{\text{X}}^4}}{{R_{\text{s}}^2 \times {\text{T}}_{\text{s}}^4}}\)
OR
\({R_{\text{X}}} = \sqrt {\frac{{{L_{\text{X}}}{\text{T}}_{\text{s}}^4}}{{{L_s}{\text{T}}_{\text{X}}^4}}} \times {R_{\text{s}}}\)
\({R_{\text{X}}} = \sqrt {\frac{{35 \times {{6000}^4}}}{{10\,{{000}^4}}}} \times {R_{\text{s}}}\) (mark for correct substitution)
RX = 2.1Rs
Allow ECF from (b)(i).
Accept values in the range: 2.0 to 2.3Rs.
Allow TS in the range: 5500 K to 6500 K.
[3 marks]
MX = \({(35)^{\frac{1}{{3.5}}}}\)Ms
MX = 2.8Ms
Allow ECF from (b)(i).
Do not accept MX = (35)\(^{\frac{1}{{3.5}}}\) for first marking point.
Accept values in the range: 2.6 to 2.9Ms.
[2 marks]
the star «core» collapses until the «inward and outward» forces / pressures are balanced
the outward force / pressure is due to electron degeneracy pressure «not radiation pressure»
[2 marks]
Examiners report
This question is about the density of the universe.
Explain, with reference to the possible fate of the universe, the significance of the critical density of matter in the universe.
Suggest one reason why it is difficult to estimate the density of matter in the universe.
Markscheme
if less than critical density, universe expands without limit;
if equal to critical density universe stops expanding after an infinite amount of time;
if greater than critical density, universe expands first then contracts;
Award [1 max] if terms open, flat and closed are used and not defined.
there is matter that cannot be detected;
which is likely to consist of dark matter/neutrinos;
or
difficulty of measuring volume accurately;
because of difficulty of measuring distances accurately;
or
matter is not evenly distributed;
so density may vary from place to place;
Examiners report
A particular emission line in a distant galaxy shows a redshift z = 0.084.
The Hubble constant is H0 = 68 km s–1 Mpc–1.
Describe what is meant by the Big Bang model of the universe.
State two features of the cosmic microwave background (CMB) radiation which are consistent with the Big Bang model.
Determine the distance to the galaxy in Mpc.
Describe how type Ia supernovae could be used to measure the distance to this galaxy.
Markscheme
theory in which all space/time/energy/matter were created at a point/singularity
at enormous temperature
with the volume of the universe increasing ever since or the universe expanding
OWTTE
[2 marks]
CMB has a black-body spectrum
wavelength stretched by expansion
is highly isotropic/homogenous
but has minor anisotropies predicted by BB model
T «= 2.7 K» is close to predicted value
For MP4 and MP5 idea of “prediction” is needed
[2 marks]
\(\frac{v}{c} = z \Rightarrow v = 0.084 \times 3 \times {10^5} = 2.52 \times {10^4}\) «km\(\,\)s–1»
\(d = \frac{v}{{{H_0}}} = \frac{{2.52 \times {{10}^4}}}{{68}} = 370.6 \approx 370\) «Mpc»
Allow ECF from MP1 to MP2.
[2 marks]
type Ia have a known luminosity/are standard candles
measure apparent brightness
determine distance from d = \(\sqrt {\frac{L}{{4\pi b}}} \)
Must refer to type Ia. Do not accept other methods (parallax, Cepheids)
[3 marks]
Examiners report
A spectral line in the light received from a distant galaxy shows a redshift of z = 0.16.
State two characteristics of the cosmic microwave background (CMB) radiation.
The present temperature of the CMB is 2.8 K. Calculate the peak wavelength of the CMB.
Describe how the CMB provides evidence for the Hot Big Bang model of the universe.
Determine the distance to this galaxy using a value for the Hubble constant of H0 = 68 km s–1\(\,\)Mpc–1.
Estimate the size of the Universe relative to its present size when the light was emitted by the galaxy in (c).
Markscheme
black body radiation / 3 K
highly isotropic / uniform throughout
OR
filling the universe
Do not accept: CMB provides evidence for the Big Bang model.
[2 marks]
«\(\lambda = \frac{{2.9 \times {{10}^{ - 3}}}}{{2.8}}\)» ≈ 1.0 «mm»
[1 mark]
the universe is expanding and so the wavelength of the CMB in the past was much smaller
indicating a very high temperature at the beginning
[2 marks]
«\(z = \frac{v}{c} \Rightarrow \)» v = 0.16 × 3 × 105 «= 0.48 × 105 km\(\,\)s−1»
«\(d = \frac{v}{{{H_0}}} \Rightarrow v = \frac{{0.48 \times {{10}^5}}}{{68}} = 706\)» ≈ 710 «Mpc»
Award [1 max] for POT error.
[2 marks]
\(z = \frac{R}{{{R_0}}} - 1 \Rightarrow \frac{R}{{{R_0}}} = 1.16\)
\(\frac{{{R_0}}}{R} = 0.86\)
[2 marks]
Examiners report
The Hubble constant is accepted to be 70 km s–1 Mpc–1. This value of the Hubble constant gives an age for the universe of 14.0 billion years.
The accepted value of the Hubble constant has changed over the past decades.
The redshift of a galaxy is measured to be z = 0.19.
Explain how international collaboration has helped to refine this value.
Estimate, in Mpc, the distance between the galaxy and the Earth.
Determine, in years, the approximate age of the universe at the instant when the detected light from the distant galaxy was emitted.
Markscheme
experiments and collecting data are extremely costly
data from many projects around the world can be collated
OWTTE
[1 mark]
v = «zc = 0.19 × 3 × 108 =» 5.7 × 107 «ms–1»
d = «\(\frac{v}{{{H_0}}} = \frac{{5.7 \times {{10}^4}}}{{70}}\)» = 810Mpc OR 8.1× 108 pc
Correct units must be present for MP2 to be awarded.
Award [2] for BCA.
[2 marks]
ALTERNATIVE 1
\(\frac{{{R_{{\text{now}}}}}}{{{R_{{\text{then}}}}}}\) = 1 + z = 1.19
so (assuming constant expansion rate) \(\frac{{{t_{{\text{now}}}}}}{t}\) = 1.19
t = \(\frac{{14}}{{1.19}}\) = 11.7By = 12«By (billion years)»
ALTERNATIVE 2
light has travelled a distance: (810 × 106 × 3.26 =) 2.6 × 109ly
so light was emitted: 2.6 billion years ago
so the universe was 11.4 billion years old
MP1 can be awarded if MP2 clearly seen.
Accept 2.5 × 1025 m for mp1.
MP1 can be awarded if MP2 clearly seen.
[3 marks]
Examiners report
This question is about determining the distance to a nearby star.
Two photographs of the night sky are taken, one six months after the other. When the photographs are compared, one star appears to have shifted from position A to position B, relative to the other stars.
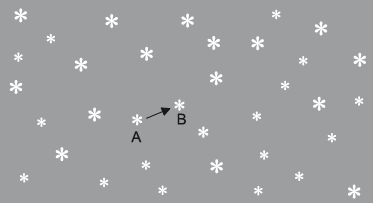
The observed angular displacement of the star is \(\theta \) and the diameter of the Earth’s orbit is \(d\). The distance from the Earth to the star is \(D\).
Outline why the star appears to have shifted from position A to position B.
Draw a diagram showing \(d\), \(D\) and \(\theta \).
Explain the relationship between \(d\), \(D\) and \(\theta \).
One consistent set of units for \(D\) and \(\theta \) are parsecs and arc-seconds. State one other consistent set of units for this pair of quantities.
Suggest whether the distance from Earth to this star can be determined using spectroscopic parallax.
Markscheme
the star is (much) closer than the other star (and close enough to Earth) / parallax effect has been observed;
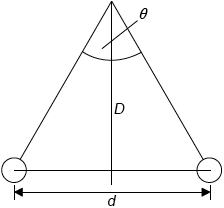
Award [1] if all three (d, D, \(\theta \)) are shown correctly.
Do not allow d shown as the radius.
Accept D as a line from Earth to the star.
\(\sin \frac{\theta }{2} = \frac{d}{{2D}}\) or \(\tan \frac{\theta }{2} = \frac{d}{{2D}}\) or \(\theta = \frac{d}{D}\);
consistent explanation, eg: small angle of approximation yields \(\theta = \frac{d}{D}\);
Allow ECF from (b)(i), eg: if d shown as radius.
any angular unit quoted for \(\theta \) and any linear unit quoted for \(D\);
(yes) star is close enough (in local galaxy) to determine spectral characteristics;
Note: not the same question as HL.
Examiners report
Well discriminating question, better candidates realized that the star is closer to Earth and drew the diagram. Many candidates made a mistake to present diameter and the angle, giving half of the proper values. The relationships were generally well explained. In the alternative pair of quantities many candidates stated only the quantity for distance, not for the angle. The HL question related to Hubble’s law was properly answered only by better candidates. The SL question was poorly answered with most confusing stellar and spectroscopic parallax.
Well discriminating question, better candidates realized that the star is closer to Earth and drew the diagram. Many candidates made a mistake to present diameter and the angle, giving half of the proper values. The relationships were generally well explained. In the alternative pair of quantities many candidates stated only the quantity for distance, not for the angle. The HL question related to Hubble’s law was properly answered only by better candidates. The SL question was poorly answered with most confusing stellar and spectroscopic parallax.
Well discriminating question, better candidates realized that the star is closer to Earth and drew the diagram. Many candidates made a mistake to present diameter and the angle, giving half of the proper values. The relationships were generally well explained. In the alternative pair of quantities many candidates stated only the quantity for distance, not for the angle. The HL question related to Hubble’s law was properly answered only by better candidates. The SL question was poorly answered with most confusing stellar and spectroscopic parallax.
Well discriminating question, better candidates realized that the star is closer to Earth and drew the diagram. Many candidates made a mistake to present diameter and the angle, giving half of the proper values. The relationships were generally well explained. In the alternative pair of quantities many candidates stated only the quantity for distance, not for the angle. The HL question related to Hubble’s law was properly answered only by better candidates. The SL question was poorly answered with most confusing stellar and spectroscopic parallax.
Well discriminating question, better candidates realized that the star is closer to Earth and drew the diagram. Many candidates made a mistake to present diameter and the angle, giving half of the proper values. The relationships were generally well explained. In the alternative pair of quantities many candidates stated only the quantity for distance, not for the angle. The HL question related to Hubble’s law was properly answered only by better candidates. The SL question was poorly answered with most confusing stellar and spectroscopic parallax.
This question is about the Big Bang model and red-shift.
In the 1960s, Penzias and Wilson discovered a uniform cosmic background radiation (CMB) in the microwave region of the electromagnetic spectrum.
Describe what is meant by the Big Bang model.
(i) Explain how the CMB is consistent with the Big Bang model.
(ii) State why the red-shift of light from galaxies supports the Big Bang model.
Markscheme
space and time originated from a single point in a large explosion / an expanding universe that originated from a single point / OWTTE;
(i) temperature of the universe immediately after the Big Bang was very high;
as it expanded it cooled down;
the wavelength of the CMB corresponds to a temperature consistent with this cooling down / OWTTE;
red shift is due to expansion of universe;
(ii) indicates that the universe is expanding;
Examiners report
Many candidates knew what is meant by the Big Bang Model.
An understanding of CMB in and its relevance to the Big Bang Model was only demonstrated by a minority of candidates. In (b) (ii) it was not sufficient to say that galaxies are moving away from Earth; a statement to the effect that the universe is expanding was required.
The collision of two galaxies is being studied. The wavelength of a particular spectral line from the galaxy measured from Earth is 116.04 nm. The spectral line when measured from a source on Earth is 115.00 nm.
Outline one reason for the difference in wavelength.
Determine the velocity of the galaxy relative to Earth.
Markscheme
galaxies are moving away
OR
space «between galaxies» is expanding
Do not accept just red-shift
«\(\frac{{\Delta \lambda }}{\lambda } = \)» \(\frac{{1.04}}{{115}} = \frac{v}{c}\)
0.009c
Accept 2.7×106 «m s–1»
Award [0] if 116 is used for \(\lambda \)
Examiners report
This question is about the development of the universe.
Light from distant galaxies, as seen by an observer on Earth, shows a red-shift. Outline why this observation suggests that the universe is expanding.
The future development of the universe is determined by the relationship between the apparent density of the universe and the critical density.
(i) Define the term critical density.
(ii) Discuss how the density of the universe determines its future development. Your discussion should include one problem associated with determining the density of the universe.
Markscheme
because of the Doppler effect;
light from sources moving away from an observer is observed to have a lower frequency than from the sources when stationary / redshift indicates motion away from observer/Earth;
(i) this is the value of density for which the universe will begin to contract after an infinite amount of time;
Do not accept “density at which universe is flat”.
(ii) if the density of the universe is less than the critical density it will continue expanding forever;
if the density is greater than the critical density then it will after a certain amount of time begin to contract;
the behaviour of galaxies suggests that there is more matter in the universe than is actually observed; { (allow other relevant comment about dark matter)
without knowing the mass of this matter the density cannot be determined;
Examiners report
This question is about the night sky.
Distinguish between a stellar cluster and a constellation.
Markscheme
stars of stellar clusters are close together (in space)/bounded gravitationally;
stars of constellations are not bounded gravitationally/appear to be close together (from Earth);
Examiners report
(a) was generally well answered.
This question is about objects in the universe.
State one difference between
(i) a main sequence star and a planet.
(ii) a stellar cluster and a constellation.
State how
(i) it is known that main sequence stars are made predominantly of hydrogen.
(ii) a main sequence star remains in equilibrium despite it having a great mass.
The graph shows the variation with wavelength of the intensity of a main sequence star.

Calculate the surface temperature of this star.
Markscheme
(i) stars, and not planets, have cores undergoing fusion;
stars have much greater mass/luminosity/absolute magnitude/temperature than planets;
planets reflect starlight rather than emit;
planets in our solar system can show retrograde motion, stars cannot;
Allow other sensible answers.
(ii) stars in a stellar cluster are close to each other/kept together by gravitation, the stars in a constellation are not;
(i) the lines in the (absorption) spectrum of the star (correspond to hydrogen wavelengths);
(ii) the gravitational force that tends to collapse the star is balanced by a force due to radiation pressure;
peak wavelength is at 400 (nm); (accept answers in the range of 380 to 420 (nm))
\(T = \left( {\frac{{{\text{2.9}} \times {\text{1}}{{\text{0}}^{ - 3}}}}{{{\text{400}} \times {\text{1}}{{\text{0}}^{ - 9}}}} = } \right){\text{ 7250 (K)}}\); (accept answers in the range of 6900 to 7600 (K))
Award [2] for a bald correct answer.
Examiners report
Light reaching Earth from quasar 3C273 has z=0.16.
(i) Outline what is meant by z.
(ii) Calculate the ratio of the size of the universe when the light was emitted by the quasar to the present size of the universe.
(iii) Calculate the distance of 3C273 from Earth using Ho=68kms−1Mpc−1.
Explain how cosmic microwave background (CMB) radiation provides support for the Hot Big Bang model.
Markscheme
(i)\(z = \frac{{\Delta \lambda }}{{{\lambda _o}}}\) where Δλ is the redshift of a wavelength and λ0 is the wavelength measured at rest on Earth OR it is a measure of cosmological redshift
Do not allow just “redshift”.
(ii) \( \ll z = \frac{R}{{{R_o}}} - 1,\frac{R}{{{R_o}}} = \frac{1}{{z + 1}} \gg {\rm{so }}\frac{R}{{{R_o}}} = \ll \frac{1}{{1.16}} \gg = 0.86\)
Do not accept answer 1.16.
(iii) v=zc=0.16×3×108=4.8×104kms-1
\(d = \frac{v}{{{H_o}}} = \frac{{4.8 \times {{10}^4}}}{{68}} = 706{\rm{Mpc}}\) OR 2.2×1025m
as the universe expanded it cooled/wavelength increased
the temperature dropped to the present approximate 3K OR wavelength stretched to the present approximate 1mm
Value is required for MP2.
Examiners report
This question is about Cepheid stars.
A Cepheid star and non-Cepheid star both belong to the same distant galaxy. Explain, stating the quantities that need to be measured, how the luminosity of the non-Cepheid star may be determined.
Markscheme
measure period and average apparent brightness/magnitude of the Cepheid to determine its distance;
measuring the apparent brightness of the star gives the luminosity (since distance is now known) from L=4πd2b;
or
measure period of Cepheid to determine its (average) luminosity;
compare the apparent brightness of the star and Cepheid to find L using L∝b;
Examiners report
The peak wavelength of the cosmic microwave background (CMB) radiation spectrum corresponds to a temperature of 2.76 K.
Identify two other characteristics of the CMB radiation that are predicted from the Hot Big Bang theory.
A spectral line in the hydrogen spectrum measured in the laboratory today has a wavelength of 21cm. Since the emission of the CMB radiation, the cosmic scale factor has changed by a factor of 1100. Determine the wavelength of the 21cm spectral line in the CMB radiation when it is observed today.
Markscheme
isotropic/appears the same from every viewing angle
homogenous/same throughout the universe
black-body radiation
23 100 «cm»
OR
231 «m»
Examiners report
Describe one key characteristic of a nebula.
Beta Centauri is a star in the southern skies with a parallax angle of 8.32×10−3 arc-seconds. Calculate, in metres, the distance of this star from Earth.
Outline why astrophysicists use non-SI units for the measurement of astronomical distance.
Markscheme
made of dust and/or gas
formed from supernova
can form new stars
some radiate light from enclosed stars
some absorb light from distant stars
\(d = \frac{1}{{8.32 \times {{10}^{ - 3}}}}\) OR 120pc
120×3.26×9.46×1015=3.70×1018m
Answer must be in metres, watch for POT.
distances are so big/large OR to avoid using large powers of 10 OR they are based on convenient definitions
Examiners report
This question is about comets.
Outline the nature of a comet.
Markscheme
icy/dusty object;
moving around the Sun on a (highly) elliptical orbit;
when close to Sun likely to display atmosphere (coma)/tail;
when far from Sun (ice re-freezes and) atmosphere no longer present;
Award [2] only if it is clearly stated that the object is a part of a Solar system.
Examiners report
HL Candidates scored well. Some candidates did not refer to the Sun or other star. Only a few candidates outlined the nature of another body instead of comet, sometimes an asteroid. Some weaker answers mentioned a body just moving in space. At SL, many answers demonstrated a poor understanding of comets, ranging from parts of dead stars to asteroids to meteors and meteorites.
This question is about the expanding universe.
Since 1929 it has been thought that the universe is expanding.
State what is meant by the expansion of the universe.
Red-shift of light from distant galaxies provides evidence for an expanding universe.
(i) State one other piece of evidence in support of an expanding universe.
(ii) Explain how your answer in (b)(i) is evidence for the Big Bang model of the universe.
Markscheme
(distant) galaxies are all moving away from each other/Earth;
the distance between galaxies is increasing;
the volume/diameter/radius/scale factor of the universe is increasing;
space itself is stretching with time;
Do not accept answers such as “everything is moving away from everything else” as this is clearly not true.
(i) cosmic microwave background/CMB/CBR;
helium/hydrogen ratio/abundance;
darkness of night sky (Olbers’ paradox);
Do not accept answers that refer to Hubble’s law/red-shift of galaxies.
radiation present in the early universe was at a high temperature/short wavelength;
as the universe expanded it cooled/wavelength increased;
so the radiation present today is in the microwave region / has temperature of 2.7 K;
or
the early universe contained high energy neutrons/protons;
as the universe expanded and cooled (to 109 K) nucleosynthesis could start, producing helium;
as the temperature dropped further, nucleosynthesis stopped leaving an excess of protons/hydrogen;
the current abundance of hydrogen and helium is consistent with the predictions of the Big Bang/expansion;
or
Olbers’ paradox asks “why is the night sky dark?”;
this cannot be explained if universe is infinite and static / OWTTE;
in an expanding universe some light is red-shifted out of visible range;
in a Big Bang universe some light from distant galaxies has not reached us yet;
Examiners report
In (a) far too many candidates just repeated the question rather than stating that expansion refers to galaxies moving further apart.
CMB radiation was usually mentioned in (b)(i). The fact that CMB was a specific prediction of the Big Bang model, long before its discovery, was sometimes mentioned in (b)(ii). Most were able to refer to cooling and wavelength increase of CMB as being consistent with the Big Bang model.
Aldebaran is a red giant star with a peak wavelength of 740 nm and a mass of 1.7 solar masses.
Show that the surface temperature of Aldebaran is about 4000 K.
The radius of Aldebaran is 3.1×1010 m. Determine the luminosity of Aldebaran.
Outline how the light from Aldebaran gives evidence of its composition.
Identify the element that is fusing in Aldebaran’s core at this stage in its evolution.
Predict the likely future evolution of Aldebaran.
Markscheme
\(T = \frac{{2.9 \times {{10}^{ - 3}}}}{{740 \times {{10}^{ - 9}}}}\)
3900 K
Answer must be to at least 2SF.
L=5.67×10-8×4π×(3.1×1010)2×40004
=1.8×1029W
Accept use of 39004 to give 1.6×1029W.
absorption lines in spectra
are specific to particular elements
Accept “emission lines in spectra”.
helium
helium flash
expansion of outer shell OR surface temperature increase
planetary nebula phase
only the core remains
if below 1.4MS/Chandrasekhar limit then white dwarf
Examiners report
This question is about cosmology.
State how the observed red-shift of many galaxies is explained.
Explain how the cosmic microwave background (CMB) radiation is consistent with the Big Bang model.
Calculate the temperature of the universe when the peak wavelength of the CMB was equal to the wavelength of red light (7.0×10−7m).
Markscheme
the universe is expanding / many galaxies are moving away from us;
the CMBR fills all of space / is uniform / is distributed equally, consistent with an “explosion” (at start of universe);
the temperature of the radiation (2.7 K) is consistent with cooling due to expansion/redshift;
\({\lambda _{\max }} = \frac{{2.9 \times 10 - 3}}{T} \Rightarrow T = \frac{{2.9 \times {{10}^{ - 3}}}}{{7.0 \times {{10}^{ - 7}}}}\);
T = 4100K;
Examiners report
This question is about some of the properties of the star Aldebaran and also about galactic distances.
Aldebaran is a red giant star in the constellation of Taurus.
(i) Describe the differences between a constellation and a stellar cluster.
(ii) Define the luminosity of a star.
(iii) The apparent brightness of Aldebaran is 3.3 ×10–8 W m–2 and the luminosity of the Sun is 3.9 ×1026 W. The luminosity of Aldebaran is 370 times that of the Sun. Show that Aldebaran is at a distance of 19 pc from Earth. (1 pc=3.1 × 1016 m)
Distances to galaxies may be determined by using Cepheid variable stars.
By considering the nature and properties of Cepheid variable stars, explain how such stars are used to determine galactic distances.
Markscheme
(i) a constellation is a collection of stars that form a (recognizable) pattern (as viewed from Earth);
the distances between the stars may be very large;
a stellar cluster is a group of stars held together by (mutual) gravitational attraction/gravity/are physically relatively close;
there can be many thousands of stars in the cluster;
all stars in the cluster were created about the same time;
(ii) the (total) power radiated/emitted/produced (by the star);
(iii) luminosity of Aldebaran = 370×3.9×1026=1.44×1029 W;
\( = \sqrt {\frac{{1.44 \times {{10}^{29}}}}{{4\pi \times 3.3 \times {{10}^{ - 8}}}}} = 5.9 \times {10^{17}}\);
\( = \frac{{5.9 \times {{10}^{17}}}}{{3.1 \times {{10}^{16}}}} = 19{\rm{pc}}\);
the (outer layers of the star) undergo a (periodic) expansion and contraction;
which produces a (periodic) variation in its luminosity/apparent brightness;
the (average) luminosity depends on the period of variation;
by measuring the period, the luminosity can be found;
by then measuring its apparent brightness, its distance from Earth can be found;
Examiners report
This question is about cosmology.
Theoretical studies indicate that the universe may be open, closed or flat.
(i) State, by reference to critical density, the condition that must be satisfied for the universe to be flat.
(ii) In a flat universe, the rate of expansion would be slowing down. Suggest a reason for this.
(iii) Outline why it has been difficult to determine whether the universe is open, closed or flat.
Outline one piece of experimental evidence that supports the fact that the universe is expanding.
Markscheme
(i) a universe whose density is equal to the critical density;
(ii) the mutual gravitational attraction would slow the expansion down;
(iii) the density of the universe needs to be determined;
this involves many uncertainties related to measurement of distances/volume;
this involves many uncertainties related to presence of dark matter;
light from galaxies is observed to be red-shifted/to have a longer wavelength than that emitted;
indicating that the distance between galaxies is getting bigger/galaxies move away from each other/from us;
Award [1 max] if galaxies are not mentioned.
or
the presence of the cosmic microwave background radiation;
is evidence of cooling of the universe/increase in wavelength/red-shift due to expansion;
Examiners report
This question is about cosmology.
Newton assumed that the universe was infinite, uniform and static. The Big Bang model suggests space and time originated at one point around 14 billion years ago. At this time the temperature was very high.
In 1965, Penzias and Wilson discovered cosmic radiation with a wavelength that corresponded to a temperature of around 3 K. Outline how cosmic radiation in the microwave region is consistent with the Big Bang model.
Markscheme
the temperature has cooled considerably since the Big Bang / the Big Bang model predicted cooling and the present temperature;
this cooling was caused by the expansion of the universe/the stretching of spacetime;
Examiners report
Most could not link the CBR causatively with the Big Bang in (b).
This question is about variable stars and supernovae.
Cepheid variable stars are used as “standard candles” by astronomers.
(i) State what is meant by a standard candle.
(ii) Outline the properties of a Cepheid star that allow it to be used as a standard candle.
(iii) Explain how astronomers use their observations of a Cepheid star to determine the distance from the star to Earth.
Markscheme
(i) object of known luminosity/power;
(ii) luminosity varies with time in a regular way;
(average) luminosity related to period of variation;
high luminosity so visible from great distances;
(iii) the period of the variation of luminosity/apparent brightness/apparent magnitude is measured;
the luminosity/absolute magnitude is determined from period;
apparent magnitude/brightness is measured (on Earth);
m-M=51g\(\left( {\frac{d}{{10}}} \right)\) or \(b = \frac{L}{{4\pi {d^2}}}\) is used to compute d;
Examiners report
(i) was very poorly done. Some candidates described a standard candle as a star that changes brightness, i.e. a Cepheid variable.
(ii) most candidates knew that Cepheid variables change luminosity in a periodic way, but few mentioned that their luminosity is high and so they are visible from great distances.
Often the general concept seemed known to the candidate in (iii) but the actual practical procedure was not specified.
This question is about cosmic microwave background (CMB) radiation.
One of Newton’s assumptions was that the universe is static. The peak intensity of the cosmic microwave background (CMB) radiation has a wavelength of 1.06 mm.
Show that this corresponds to a temperature around 3 K.
Suggest how the discovery of the CMB in the microwave region contradicts Newton’s assumption of the static universe.
Markscheme
\(T = \frac{{2.90 \times {{10}^{ - 3}}}}{{{\lambda _{\max }}}} = \frac{{2.90 \times {{10}^{ - 3}}}}{{1.06 \times {{10}^{ - 3}}}}\);
\( = 2.7{\text{ K}}\);
Must show 2 sig figs or more, as 3 K is given.
current low temperature observed is a result of expansion;
(expansion) has caused cooling from high temperatures;
Examiners report
Well done by candidates, weaker candidates did not write their ideas clearly enough in (a)(ii). Part (b) was also quite well done, but only better candidates mentioned uncertainty in measurement of distances to galaxies. At SL the calculation of the temperature of the CMB was successful for most candidates, however, relating it to Newton’s static universe polarised candidates into non-answers or correct answers.
Well done by candidates, weaker candidates did not write their ideas clearly enough in (a)(ii). Part (b) was also quite well done, but only better candidates mentioned uncertainty in measurement of distances to galaxies. At SL the calculation of the temperature of the CMB was successful for most candidates, however, relating it to Newton’s static universe polarised candidates into non-answers or correct answers.
This question is about the characteristics of the stars Procyon A and Procyon B.
The stars Procyon A and Procyon B are both located in the same stellar cluster in the constellation Canis Minor. Distinguish between a constellation and a stellar cluster.
Constellation:
Stellar cluster:
Markscheme
constellation:
a collection/group of stars that form a recognizable pattern (as viewed from Earth) / a group/pattern of stars not close together (in space);
stellar cluster:
a group of stars (including gas and dust) held together by gravity/forming a globular/open arrangement / a group of stars close to each other (in space);
Examiners report
A large number of candidates were able to correctly distinguish between a constellation and a stellar cluster.
This question is about a particular star called Barnard’s star.
The peak wavelength in the spectrum of Barnard’s star is 940 nm. The following data are available.
\[\frac{{{\text{apparent brightness of Barnard's star}}}}{{{\text{apparent brightness of the Sun}}}} = 2.5 \times {10^{ - 14}}\]
\[\frac{{{\text{luminosity of Barnard's star}}}}{{{\text{luminosity of the Sun}}}} = 3.8 \times {10^{ - 3}}\]
(i) Show that the surface temperature of Barnard’s star is about 3000 K.
(ii) Suggest why Barnard’s star is not likely to be either a white dwarf or a red giant.
(i) Determine, in astronomical units (AU), the distance between Earth and Barnard’s star.
(ii) Calculate the parallax angle for Barnard’s star as observed from Earth.
(iii) Outline how the parallax angle is measured.
Markscheme
(i) \(T = \frac{{0.0029}}{\lambda }\);
3080/3090 (K); (more than 1 SD must be shown)
(ii) temperature too low for white dwarf;
not luminous enough for red giant;
(i) \(L = 4\pi {d^2}b\);
\(\frac{{{d_B}}}{{{d_S}}}\left( { = \sqrt {\frac{{{L_B}}}{{{L_S}}}\frac{{{b_S}}}{{{b_B}}}} } \right) = \sqrt {\frac{{3.8 \times {{10}^{ - 3}}}}{{2.5 \times {{10}^{ - 14}}}}} \);
3.9×105 AU;
(ii) conversion of AU to 1.89 pc;
0.53 (arc-seconds);
with respect to fixed background;
with six months between readings;
parallax angle is half the total angle / OWTTE;
May be shown in a diagram.
Examiners report
This question is about the cosmic microwave background (CMB) radiation.
State two characteristics of the cosmic microwave background (CMB) radiation.
1.
2.
Explain how CMB radiation is evidence for the Big Bang model of an expanding universe.
Markscheme
electromagnetic radiation in the microwave region;
black body radiation (at a temperature of about 3 K);
(almost) isotropic/uniform radiation;
radiation that fills the universe/exists everywhere/has no obvious point of origin;
CMB radiation was a prediction of the Big Bang model;
CMB “temperature” is consistent with a universe that has cooled from an initial hot state;
CMB wavelength is consistent with a universe that has expanded from an initial hot, dense state;
CMB isotropy/uniformity is consistent with its origin in the very early universe;
Examiners report
This question is about stellar radiation and stellar types.
Alnilam and Bellatrix are two stars in the constellation of Orion. The table gives information on each of these stars. \({L_ \odot }\) is the luminosity of the Sun and \({R_ \odot }\) is the radius of the Sun.

Using a telescope based on Earth, an observer estimates the distance to Alnilam using the stellar parallax method.
Describe the stellar parallax method.
Markscheme
the position of the star (relative to the fixed background) is measured six months apart/January to July;
the parallax angle p can be used to determine the distance using d = \(\frac{1}{p}\);
Examiners report
(b)(i) was mostly well answered.
This question is about the Hertzsprung–Russell (HR) diagram and the Sun.
A Hertzsprung–Russell (HR) diagram is shown.

The following data are given for the Sun and a star Vega.
Luminosity of the Sun \( = 3.85 \times {10^{26}}{\text{ W}}\)
Luminosity of Vega \( = 1.54 \times {10^{28}}{\text{ W}}\)
Surface temperature of the Sun \( = 5800{\text{ K}}\)
Surface temperature of Vega \( = 9600{\text{ K}}\)
Determine, using the data, the radius of Vega in terms of solar radii.
Outline how observers on Earth can determine experimentally the temperature of a distant star.
Markscheme
\(\frac{{{L_{\text{V}}}}}{{{L_{\text{S}}}}} = \left( {\frac{{\sigma {A_{\text{V}}}{{[{T_{\text{V}}}]}^4}}}{{\sigma {A_{\text{S}}}{{[{T_{\text{S}}}]}^4}}} = } \right)\frac{{\sigma {{[{r_{\text{V}}}]}^2}{{[{T_{\text{V}}}]}^4}}}{{\sigma {{[{r_{\text{S}}}]}^2}{{[{T_{\text{S}}}]}^4}}}\);
\(\frac{{1.54 \times {{10}^{28}}}}{{3.85 \times {{10}^{26}}}} = \frac{{{{[{r_{\text{V}}}]}^2}}}{{{{[{r_S}]}^2}}} \times \frac{{{{9600}^4}}}{{{{5800}^4}}}\);
\({r_{\text{V}}} = \left( {\sqrt {\frac{{1.54 \times {{10}^{28}}}}{{3.85 \times {{10}^{26}}}} \times \frac{{{{5800}^4}}}{{{{9600}^4}}}} {r_S} = } \right){\text{ 2.3 }}{r_{\text{S}}}\);
Do not award third marking point if radius of the Sun is lost.
obtain the spectrum of the star;
measure the position of the wavelength corresponding to maximum intensity;
use Wien’s law (to determine temperature); } (allow quotation of Wien’s equation if symbols defined)
Award [3 max] for referring to identification of temperature via different ionizations of different elements.
Examiners report
candidates notably addressed absolute magnitude without referring to apparent magnitude as the question asked. Well-prepared candidates (both HL and SL) only had a problem with the part related to the use of a non-linear temperature scale. Average prepared candidates displayed difficulty in the experimental measurement of the temperature of the distant star and also with details of nuclear processes occurring in the Sun during transformation to a red giant.
candidates notably addressed absolute magnitude without referring to apparent magnitude as the question asked. Well-prepared candidates (both HL and SL) only had a problem with the part related to the use of a non-linear temperature scale. Average prepared candidates displayed difficulty in the experimental measurement of the temperature of the distant star and also with details of nuclear processes occurring in the Sun during transformation to a red giant.
This question is about the development of the universe.
Define, with reference to the flat model of the universe, critical density.
The diagram represents how the universe might develop if its density were greater than the critical density.
The dotted line represents the development of the universe if the density of the universe were zero.
On the diagram above,
(i) label with the letter N the present time.
(ii) draw a line labelled F to represent the development of the universe corresponding to a flat universe.
(iii) draw a line labelled O to represent the development of the universe corresponding to the universe if its density were less than the critical density.
Markscheme
critical density is the density for which the universe stops expanding;
after an infinite amount of time;
radius of the universe
(i) the time corresponding to where the two lines touch; {(labelled N on the time axis or the graph)
(ii) a slightly curved line between the dotted line and the closed universe line;
(labelled F)
(iii) a slightly curved line between the dotted line and the flat universe line;
(labelled O)
Allow an accelerating universe graph labelled either F or O.
Examiners report
The diagram shows the structure of a typical main sequence star.
Star X is likely to evolve into a neutron star.
State the most abundant element in the core and the most abundant element in the outer layer.
The Hertzsprung–Russell (HR) diagram shows two main sequence stars X and Y and includes lines of constant radius. R is the radius of the Sun.
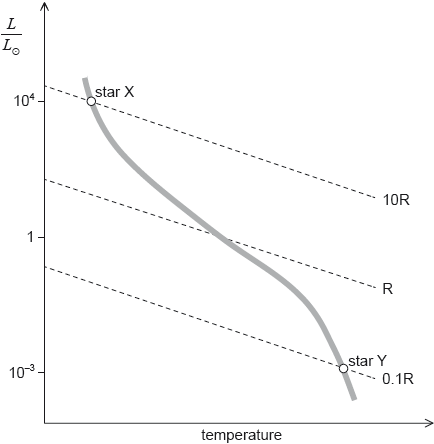
Using the mass–luminosity relation and information from the graph, determine the ratio \(\frac{{{\text{density of star X}}}}{{{\text{density of star Y}}}}\).
On the HR diagram in (b), draw a line to indicate the evolutionary path of star X.
Outline why the neutron star that is left after the supernova stage does not collapse under the action of gravitation.
The radius of a typical neutron star is 20 km and its surface temperature is 106 K. Determine the luminosity of this neutron star.
Determine the region of the electromagnetic spectrum in which the neutron star in (c)(iii) emits most of its energy.
Markscheme
core: helium
outer layer: hydrogen
Accept no other elements.
[2 marks]
ratio of masses is \({\left( {\frac{{{{10}^4}}}{{{{10}^{ - 3}}}}} \right)^{\frac{1}{{3.5}}}} = {10^2}\)
ratio of volumes is \({\left( {\frac{{10}}{{{{10}^{ - 1}}}}} \right)^3} = {10^6}\)
so ratio of densities is \(\frac{{{{10}^2}}}{{{{10}^6}}} = {10^{ - 4}}\)
Allow ECF for MP3 from earlier MPs
[3 marks]
line to the right of X, possibly undulating, very roughly horizontal
Ignore any paths beyond this as the star disappears from diagram.
[1 mark]
gravitation is balanced by a pressure/force due to neutrons/neutron degeneracy/pauli exclusion principle
Do not accept electron degeneracy.
[1 mark]
L = \(\sigma \)AT 4 = 5.67 x 10–8 x 4\(\pi \) x (2.0 x 104)2 x (106)4
L = 3 x 1026 «W»
OR
L = 2.85 x 1026 «W»
Allow ECF for [1 max] if \(\pi \)r 2 used (gives 7 x 1026 «W »)
Allow ECF for a POT error in MP1.
[2 marks]
\(\lambda = \frac{{2.9 \times {{10}^{ - 3}}}}{{{{10}^6}}} = 2.9 \times {10^{ - 9}}\) «m»
this is an X-ray wavelength
[2 marks]
Examiners report
This question is about the life history of stars.
Outline, with reference to pressure, how a star on the main sequence maintains its stability.
Markscheme
balance of two forces/pressures;
(balance) between radiation/pressure and gravitational force/pressure;
(radiation pressure is when) photons/radiation exert outwards force on nuclei/ particles;
(gravitational pressure is when) gravitational force between particles/layers of the star acts inwards;
Examiners report
(a) There was evidence of superficial learning from the syllabus. Only a few of the best candidates wrote details of radiation and/or gravitational pressure, in response to the “outline” command term.
The following data apply to the star Gacrux.
\[\begin{array}{*{20}{l}}
{{\text{Radius}}}&{ = 58.5 \times {{10}^9}{\text{ m}}} \\
{{\text{Temperature}}}&{ = 3600{\text{ K}}} \\
{{\text{Distance}}}&{ = 88{\text{ ly}}}
\end{array}\]
A Hertzsprung–Russell (HR) diagram is shown.
On the HR diagram,
Main sequence stars are in equilibrium under the action of forces. Outline how this equilibrium is achieved.
A main sequence star P, is 1.3 times the mass of the Sun. Calculate the luminosity of P relative to the Sun.
The luminosity of the Sun L\(_ \odot \) is 3.85 × 1026 W. Determine the luminosity of Gacrux relative to the Sun.
The distance to Gacrux can be determined using stellar parallax. Outline why this method is not suitable for all stars.
draw the main sequence.
plot the position, using the letter P, of the main sequence star P you calculated in (b).
plot the position, using the letter G, of Gacrux.
Discuss, with reference to its change in mass, the evolution of star P from the main sequence until its final stable phase.
Markscheme
photon/fusion/radiation force/pressure balances gravitational force/pressure
gives both directions correctly (outwards radiation, inwards gravity)
OWTTE
[2 marks]
«L \( \propto \) M35 for main sequence»
luminosity of P = 2.5 «luminosity of the Sun»
[1 mark]
LGacrux = 5.67 × 10–8 × 4π × (58.5 × 109)2 × 36004
LGacrux = 4.1 × 10–29 «W»
\(\frac{{{L_{Gacrux}}}}{{{L_ \odot }}}\) «= \(\frac{{4.1 \times {{10}^{29}}}}{{3.85 \times {{10}^{26}}}}\)» = 1.1 × 103
[3 marks]
if the star is too far then the parallax angle is too small to be measured
OR
stellar parallax is limited to closer stars
OWTTE
[1 mark]
line or area roughly inside shape shown – judge by eye
Accept straight line or straight area at roughly 45°

[1 mark]
P between \(1{L_ \odot }\) and \({10^1}{L_ \odot }\) on main sequence drawn
[1 mark]
at \({10^3}{L_ \odot }\), further to right than 5000 K and to the left of 2500 K (see shaded region)
[1 mark]
ALTERNATIVE 1
Main sequence to red giant
planetary nebula with mass reduction/loss
OR
planetary nebula with mention of remnant mass
white dwarf
ALTERNATIVE 2
Main sequence to red supergiant region
Supernova with mass reduction/loss
OR
Supernova with mention of remnant mass
neutron star
OR
Black hole
OWTTE for both alternatives
[3 marks]
Examiners report
The first graph shows the variation of apparent brightness of a Cepheid star with time.
The second graph shows the average luminosity with period for Cepheid stars.
Determine the distance from Earth to the Cepheid star in parsecs. The luminosity of the Sun is 3.8 × 1026 W. The average apparent brightness of the Cepheid star is 1.1 × 10–9 W m–2.
Explain why Cephids are used as standard candles.
Markscheme
from first graph period=5.7 «days» ±0.3 «days»
from second graph \(\frac{L}{{{L_{{\text{SUN}}}}}} = 2300\) «\( \pm {\text{200}}\)»
d = «\(\sqrt {\frac{{2500 \times 3.8 \times {{10}^{26}}}}{{4\pi \times 1.1 \times {{10}^{ - 9}}}}} = 8.3 \times {10^{18}}{\text{m}}\)» =250 «pc»
Accept answer from interval 240 to 270 pc If unit omitted, assume pc.
Watch for ECF from mp1
Cepheids have a definite/known «average» luminosity
which is determined from «measurement of» period
OR
determined from period-luminosity graph
Cepheids can be used to estimate the distance of galaxies
Do not accept brightness for luminosity.
Examiners report
This question is about the properties of a star.
The peak in the radiation spectrum of a star X is at a wavelength of 300 nm.
Show that the surface temperature of star X is about 10000 K.
The radius of star X is 4.5 RS where RS is the radius of the Sun. The surface temperature of the Sun is 5.7×103 K.
Determine the ratio \(\frac{{{\rm{luminosity of star X}}}}{{{\rm{luminosity of the Sun}}}}\).
On the Hertzsprung–Russell diagram, label the position of star X with the letter X.
Markscheme
\(T = \frac{{2.9 \times {{10}^{ - 3}}}}{{3.0 \times {{10}^{ - 7}}}}\);
9700 (K);
\(\frac{{{L_X}}}{{{L_S}}} = \frac{{\sigma {r_x}^2{T_x}^4}}{{\sigma {r_S}^2{T_S}^4}}\);
=\(\frac{{{{4.5}^2} \times {{9700}^4}}}{{{{5700}^4}}}\);
=170;
Accept answers that use T = 10000(K) to give an answer of 190.
X marked correctly within range shown;
Examiners report
Was very well done in general.
Many answered (b) well, but a large minority made mistakes with powers or tried to evaluate both luminosities then find the ratio and failed in the process. A lot of poor algebra and messy working was evident.
Was well done in general.
This question is about the Hertzsprung–Russell (HR) diagram and using it to determine some properties of stars.
The diagram below shows the grid of a HR diagram, on which the positions of selected stars are shown. (LS = luminosity of the Sun.)
(i) Draw a circle around the stars that are red giants. Label this circle R.
(ii) Draw a circle around the stars that are white dwarfs. Label this circle W.
(iii) Draw a line through the stars that are main sequence stars.
Explain, without doing any calculation, how astronomers can deduce that star B has a larger diameter than star A.
Using the following data and information from the HR diagram, show that star A is at a distance of about 800 pc from Earth.
Apparent brightness of the Sun =1.4×103Wm−2
Apparent brightness of star A = 4.9×10−9Wm−2
Mean distance of Sun from Earth =1.0 AU
1 pc = 2.1×105AU
Explain why the distance of star A from Earth cannot be determined by the method of stellar parallax.
Markscheme
(i) circle labelled R as shown above;
Accept answers that include the star B within the circle.
(ii) circle labelled W as shown above;
(iii) any line (not necessarily straight) going from top left to bottom right, through or near all or most of stars;
star B has lower temperature;
star B has (slightly) larger luminosity / stars have approximately same luminosity;
surface area calculated from L=σAT4, so star B has larger surface area/diameter / to give the same/similar luminosity at lower temperature, star B must have bigger diameter/surface area;
(from HR diagram) LA =105LS;
\(b = \frac{L}{{4\pi {d^2}}}\) used;
to give \(\frac{{{d_{\rm{A}}}}}{{{d_{\rm{S}}}}} = \sqrt {\frac{{{L_{\rm{A}}}}}{{{L_{\rm{S}}}}} \times \frac{{{b_{\rm{S}}}}}{{{b_{\rm{A}}}}}} = \sqrt {{{10}^5} \times \frac{{1.4 \times {{10}^3}}}{{4.9 \times {{10}^{ - 9}}}}} \);
hence dA =1.7×108 AU;
= 800 pc
Do not award a mark for the conversion from AU to pc.
the parallax angle is too small to be measured accurately / the distance is greater than the limit for stellar parallax, which is 100 pc;
Accept any value from 100–800 pc for limit. Do not accept “it’s too far away”.
Examiners report
Alpha Centauri A and B is a binary star system in the main sequence.
State what is meant by a binary star system.
(i) Calculate \(\frac{{{b_{\text{A}}}}}{{{b_{\text{B}}}}} = \frac{{{\text{apparent brightness of Alpha Centauri A}}}}{{{\text{apparent brightness of Alpha Centauri B}}}}\).
(ii) The luminosity of the Sun is 3.8 × 1026 W. Calculate the radius of Alpha Centauri A.
Show, without calculation, that the radius of Alpha Centauri B is smaller than the radius of Alpha Centauri A.
Alpha Centauri A is in equilibrium at constant radius. Explain how this equilibrium is maintained.
A standard Hertzsprung–Russell (HR) diagram is shown.
Using the HR diagram, draw the present position of Alpha Centauri A and its expected evolutionary path.
Markscheme
two stars orbiting about a common centre «of mass/gravity»
Do not accept two stars orbiting each other.
i
stars are roughly at the same distance from Earth
OR
d is constant for binaries
\(\frac{{{L_{\rm{A}}}}}{{{L_{\rm{B}}}}} = \frac{{1.5}}{{0.5}} = 3.0\)
Award [2] for a bald correct answer.
ii
\(r = \sqrt {\frac{{1.5 \times 3.8 \times {{10}^{26}}}}{{5.67 \times {{10}^{ - 8}} \times 4\pi \times {{5800}^4}}}} \)
= 8.4 × 108 «m»
Award [2] for a bald correct answer.
«A=\(\frac{L}{{\sigma {T^4}}}\)» B and A have similar temperatures
so areas are in ratio of luminosities
«so B radius is less than A»
radiation pressure/force outwards
gravitational pressure/force inwards
forces/pressures balance
Alpha Centauri A within allowable region
some indication of star moving right and up then left and down ending in white dwarf region as indicated
Examiners report
This question is about stars in the constellation Canis Minor.
(i) Using the data in (c), calculate, in parsecs, the distance from Earth to Gomeisa.
(ii) Gomeisa has a radius four times that of the Sun. Use the data in (c) to show that the ratio
\[\frac{{{\rm{luminosity of Gomeisa}}}}{{{\rm{luminosity of Sun}}}}\]
is about 200.
Gomeisa, Luyten’s star and the Sun are main sequence stars. On the grid of the Hertzsprung–Russell (HR) diagram, identify the position of
(i) Gomeisa, with the letter G.
(ii) Luyten’s star, with the letter L.
Markscheme
(i) \(2.9 = - 0.7 + 51{\rm{g}}\left( {\frac{d}{{10}}} \right)\);
\(\frac{d}{{10}} = {10^{\frac{{{\rm{3.6}}}}{{\rm{5}}}}}\);
52 (pc);
Award [2 max] ECF if magnitudes are reversed giving 1.9 (pc).
Award [2 max] if data for Lutyen’s star is used and no credit for the distance of 4 (pc) has already been given in (c)(i).
Award [3] for a bald correct answer.
(ii) \(\frac{{{L_{\rm{G}}}}}{{{L_{\rm{S}}}}} = {\left[ {\frac{{{R_{\rm{G}}}}}{{{R_{\rm{S}}}}}} \right]^2}{\left[ {\frac{{{T_{\rm{G}}}}}{{{T_{\rm{S}}}}}} \right]^4}\);
\( = {4^2} \times {\left[ {\frac{{11000}}{{5800}}} \right]^4}\);
=210; (must see this answer to better than 1 significant figure)
Approximate answer of 200 is given in the question so correct steps in the working are required to award any marks.
(i) G correct within region shown;
(ii) L correct within region shown;
Examiners report
Sirius is a binary star. It is composed of two stars, Sirius A and Sirius B. Sirius A is a main sequence star.
The Sun’s surface temperature is about 5800 K.
The image shows a Hertzsprung–Russell (HR) diagram.
The mass of Sirius A is twice the mass of the Sun. Using the Hertzsprung–Russell (HR) diagram,
State what is meant by a binary star.
The peak spectral line of Sirius B has a measured wavelength of 115 nm. Show that the surface temperature of Sirius B is about 25 000 K.
The mass of Sirius B is about the same mass as the Sun. The luminosity of Sirius B is 2.5 % of the luminosity of the Sun. Show, with a calculation, that Sirius B is not a main sequence star.
Determine the radius of Sirius B in terms of the radius of the Sun.
Identify the star type of Sirius B.
draw the approximate positions of Sirius A, labelled A and Sirius B, labelled B.
sketch the expected evolutionary path for Sirius A.
Markscheme
two stars orbiting a common centre «of mass»
Do not accept “stars which orbit each other”
«\(\lambda \) x T = 2.9 x 10–3»
T = \(\frac{{2.9 \times {{10}^{ - 3}}}}{{115 \times {{10}^{ - 9}}}}\) = 25217 «K»
use of the mass-luminosity relationship or \({\left( {\frac{{{M_{{\text{Sirius}}}}}}{{{M_{{\text{Sun}}}}}}} \right)^{3.5}}\) = 1
if Sirius B is on the main sequence then \(\left( {\frac{{{L_{\,{\text{Sirius}}\,{\text{B}}}}}}{{L{\,_{{\text{Sun}}}}}}} \right)\) = 1 «which it is not»
Conclusion is given, justification must be stated
Allow reverse argument beginning with luminosity
\(\left( {\frac{{{L_{\,{\text{Sirius}}\,{\text{B}}}}}}{{L{\,_{{\text{Sun}}}}}}} \right)\) = 0.025
r Sirius = «\(\sqrt {0.025 \times {{\left( {\frac{{5800}}{{25000}}} \right)}^4}} \) =» 0.0085 r Sun
white dwarf
Sirius A on the main sequence above and to the left of the Sun AND Sirius B on white dwarf area as shown
Both positions must be labelled
Allow the position anywhere within the limits shown.
arrow goes up and right and then loops to white dwarf area
Examiners report
This question is about the star Naos (Zeta Puppis).
The following data are available for the star Naos.
Surface temperature = 4.24×104K
Radius = 7.70×109m
Apparent magnitude = +2.21
Parallax angle = 3.36×10–3 arcseconds
The distance to Naos may be determined by the method of stellar parallax. The diagram shows the star Naos and the Earth in its orbit around the Sun.
(i) Draw lines on the diagram above in order to indicate the parallax angle of Naos.
(ii) Outline how the parallax angle of Naos may be measured.
Markscheme
(i) either angle p as shown;
(ii) the star’s position is observed at two times, six months apart;
the shift in the star’s position relative to the distant stars is (twice) the parallax angle;
Accept correct answers which are clear from annotations on the diagram.
Examiners report
This question is about stars.
The Hertzsprung–Russell (HR) diagram shows the Sun, a star labelled A and the main sequence.
Star A is part of a binary star system. The diagram shows the orbit of star A and the orbit of its companion, star B.
The temperature of star A is TA, the temperature of star B is TB and \(\frac{{{T_A}}}{{{T_B}}} = 0.60\). The radius of star A is RA, the radius of star B is RB and \(\frac{{{R_A}}}{{{R_B}}} = 270\).
Show that the luminosity of star A is 9.4×103 times greater than the luminosity of star B.
The diagram below shows the spectrum of the stars as observed from Earth. The spectrum shows one line from star A and one line from star B, when the stars are in the position shown in the diagram (b).
On the spectrum draw lines to show the approximate positions of these spectral lines after the stars have completed one quarter of a revolution.
Markscheme
\(\frac{{{L_{\rm{A}}}}}{{{L_{\rm{B}}}}} = \frac{{\sigma 4\pi R_{\rm{A}}^2T_{\rm{A}}^4}}{{\sigma 4\pi R_{\rm{B}}^2T_{\rm{B}}^4}}\);
\(\frac{{{L_{\rm{A}}}}}{{{L_{\rm{B}}}}} = {0.60^4} \times {270^2}\) or look for 3 or more sig fig eg 9.45×103;
\(\left( {\frac{{{L_{\rm{A}}}}}{{{L_{\rm{B}}}}} = 9.4 \times {{10}^3}} \right)\)
Award [1] for each correct line.
The shifted lines are light grey in the diagram above. Ignore magnitude of shift.
Award [0] if more than two lines are drawn unless it is clear which lines are to be marked.
Examiners report
This question is about stellar distances and stellar properties.
On the grid of the Hertzsprung–Russell (HR) diagram shown, draw a line to represent the approximate position of the main sequence.
Barnard’s star is a main sequence star that is 1.8 pc from Earth.
(i) Define the parsec.
(ii) Calculate the parallax angle of Barnard’s star as measured from Earth.
Outline, using your answer to (b)(ii) and a labelled diagram, how the distance of Barnard’s star from Earth is measured.
The apparent brightness of Barnard’s star is 3.6×10–12Wm–2 and its surface temperature is 3800 K.
Given that 1 pc=3.1×1016m, show for Barnard’s star
(i) that its luminosity is of the order of 1023W.
(ii) that its surface area is of the order of 1016m2.
Markscheme
any suitable line from anywhere in top left-hand quadrant; (accept a straight line)
to bottom right-hand quadrant;
The shaded areas are the limits within which the line must be drawn.
(i) distance at which 1 AU subtends an angle of 1 arcsec / distance at which the angle subtended by the radius of Earth’s orbit is 1 arcsec;
(ii) \(p = \left( {\frac{1}{d} = } \right)0.56{\mathop{\rm arcsec}\nolimits} \);
Labelled diagram should relate to the following points:
measure against the fixed stars the angle Barnard’s star subtends at Earth in June and again in December;
difference between the two angles is twice the parallax angle;
orbital radius of Earth about Sun is 1 AU so distance to star is computed from \(d = \frac{1}{p}\);
(i) L=4πbd2;
=4×3.14×3.6×10-12×[1.8×3.1]2×1032;
=1.4×1023W;
≈1023W
(ii) \(A = \frac{L}{{\sigma {T^4}}}\);
\( = \frac{{1.4 \times {{10}^{23}}}}{{5.67 \times {{10}^{ - 8}} \times {{3.8}^4} \times {{10}^{12}}}}\); (allow ECF from (d)(i))
=1.184×1016m\(^2\);
≈1016m2
Examiners report
This question is about the development of the universe.
The graph shows one possible way in which the universe is thought to change with time. This type of universe is known as a fl at universe.
On the graph, draw lines to show the variation with time of the size of the universe for both a closed universe and an open universe. Label your line for the closed universe C and your line for the open universe O.
Explain how the open and closed outcomes for the universe depend on the critical density of matter in the universe.
State one reason why it is difficult to determine the density of the universe.
Markscheme
after present, open universe curve drawn above flat curve and closed universe curve drawn under flat curve; (both needed for mark)
all meet at “present time”;
Ignore curves before present time.
if density less than critical density/too low the universe will expand forever;
if greater than critical density the universe contracts;
after an initial expansion;
If critical density not mentioned award [1 max].
presence of dark matter / WIMPS / MACHOS etc;
Examiners report
This question is about the properties of a star.
Describe what is meant by a
(i) constellation.
(ii) stellar cluster.
On the Hertzsprung–Russell diagram above,
(i) label the position of Betelgeuse with the letter B.
(ii) sketch the position of main sequence stars.
Markscheme
(i) a collection of stars that form a recognizable group (as viewed from Earth);
that need not be/are not close to each other/gravitationally bound;
(ii) stars that are gravitationally bound/forming an open arrangement/close to each other (in space);
(i) position labelled B within shaded area;
Award [1] if label B is missing but point is clear.
(ii) generally the correct shape; (allow broad line)
Examiners report
This question is about stars.
The Hertzsprung–Russell (HR) diagram shows the position of the Sun and three stars labelled A, B and C.
State the star type for A, B and C.
Determine the ratio \(\frac{{{\rm{radius of B}}}}{{{\rm{radius of A}}}}\)
The apparent brightness of C is 3.8 \( \times \) 10–10 Wm–2. The luminosity of the Sun is 3.9 \( \times \) 1026 W.
(i) State what is meant by apparent brightness and luminosity.
Apparent brightness:
Luminosity:
(ii) Determine the distance of C from Earth.
The graph shows the variation with wavelength λ of the intensity I of the radiation emitted by 1.0m2 of the surface of the Sun. The curve of the graph has been adjusted so that the maximum intensity is 1.
On the grid, draw a corresponding graph for star C. Your curve should have a maximum intensity of 1.
Markscheme
A: white dwarf;
B: main sequence / blue giant / blue supergiant;
C: red giant / red supergiant;
\(\frac{{{R_B}}}{{{R_A}}} = {10^3}\);
Award [2] for a bald correct answer.
(i) apparent brightness: (total) power received per unit area/per m2 } (accept luminosity for power)
luminosity: (total) power radiated;
Accept energy per second instead of power.
d=2.9 \( \times \) 1019 (m);
Award [1] for 2.9×1017 (misses factor of 10000).
Award [2] for a bald correct answer.
same shape as curve in graph and displaced to right;
peak at 10 ± 2 \( \times \) 10-7 m with intensity ≤1;
Examiners report
In part (a) nearly everyone could name the types of stars.
In (b) the ratio of star radii was usually correct, with the square root missed by many candidates.
The apparent brightness and power of a star in (c)(i) were usually correctly stated. Mistakes usually involved stating power per second or energy. Part (c)(ii) was done well also, although arithmetic errors were common. In (d) nearly all candidates found the star’s peak wavelength and drew a suitable graph. Overall a very well answered question.
In (d) nearly all candidates found the star’s peak wavelength and drew a suitable graph. Overall a very well answered question.