
HL Paper 2
This question is in two parts. Part 1 is about electric fields and radioactive decay. Part 2 is about waves.
Part 1 Electric fields and radioactive decay
An ionization chamber is a device which can be used to detect charged particles.
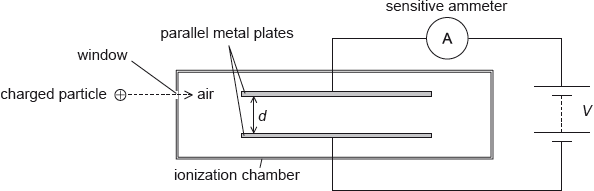
The charged particles enter the chamber through a thin window. They then ionize the air between the parallel metal plates. A high potential difference across the plates creates an electric field that causes the ions to move towards the plates. Charge now flows around the circuit and a current is detected by the sensitive ammeter.
The separation of the plates d is 12 mm and the potential difference \(V\) between the plates is 5.2 kV. An ionized air molecule M with charge \( + 2e\) is produced when a charged particle collides with an air molecule.
Radium-226 \({\text{(}}_{\;{\text{88}}}^{{\text{226}}}{\text{Ra)}}\) decays into an isotope of radon (Rn) by the emission of an alpha particle and a gamma-ray photon. The alpha particle may be detected using the ionization chamber but the gamma-ray photon is unlikely to be detected.
On the diagram, draw the shape of the electric field between the plates.
Calculate the electric field strength between the plates.
Calculate the force on M.
Determine the change in the electric potential energy of M as it moves from the positive to the negative plate.
Construct the nuclear equation for the decay of radium-226.

Radium-226 has a half-life of 1600 years. Determine the time, in years, it takes for the activity of radium-226 to fall to 5% of its original activity.
This question is in two parts. Part 1 is about gravitational force fields. Part 2 is about properties of a gas.
Part 1 Gravitational force fields
State Newton’s universal law of gravitation.
A satellite of mass m orbits a planet of mass M. Derive the following relationship between the period of the satellite T and the radius of its orbit R (Kepler’s third law).
\({T^2} = \frac{{4{\pi ^2}{R^3}}}{{GM}}\)
A polar orbiting satellite has an orbit which passes above both of the Earth’s poles. One polar orbiting satellite used for Earth observation has an orbital period of 6.00 × 103s.
Mass of Earth = 5.97 × 1024 kg
Average radius of Earth = 6.37 × 106 m
(i) Using the relationship in (b), show that the average height above the surface of the Earth for this satellite is about 800 km.
(ii) The satellite moves from an orbit of radius 1200 km above the Earth to one of radius 2500 km. The mass of the satellite is 45 kg.
Calculate the change in the gravitational potential energy of the satellite.
(iii) Explain whether the gravitational potential energy has increased, decreased or stayed the same when the orbit changes, as in (c)(ii).
This question is in two parts. Part 1 is about the use of renewable energy sources. Part 2 is about the gravitational potential of the Earth.
Part 2 Gravitational potential of the Earth
A satellite of mass 780 kg is put into circular orbit \(4.0 \times {10^3}{\text{ km}}\) above the surface of the Earth. It is then moved to a higher orbit \(3.2 \times {10^4}{\text{ km}}\) above the surface.
Calculate, for the satellite as it is moved from the lower orbit to the higher orbit, the change in
The table gives the gravitational potential V for various distances r from the surface of Earth. The radius of Earth is \(6.4 \times {10^3}{\text{ km}}\).
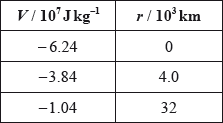
Show that the data are consistent with Earth acting as a point mass with its mass concentrated at its centre.
(i) the gravitational potential energy.
(ii) kinetic energy
(iii) total energy.
This question is in two parts. Part 1 is about collisions. Part 2 is about the gravitational field of Mars.
Part 1 Collisions
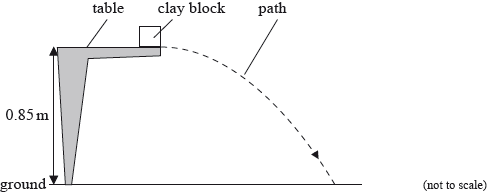
The experiment is repeated with the clay block placed at the edge of the table so that it is fired away from the table. The initial speed of the clay block is \({\text{4.3 m}}\,{{\text{s}}^{ - 1}}\) horizontally. The table surface is 0.85 m above the ground.
Part 2 Gravitational field of Mars
The graph shows the variation with distance \(r\) from the centre of Mars of the gravitational potential \(V\). \(R\) is the radius of Mars which is 3.3 Mm. (Values of \(V\) for \(r < R\) are not shown.)
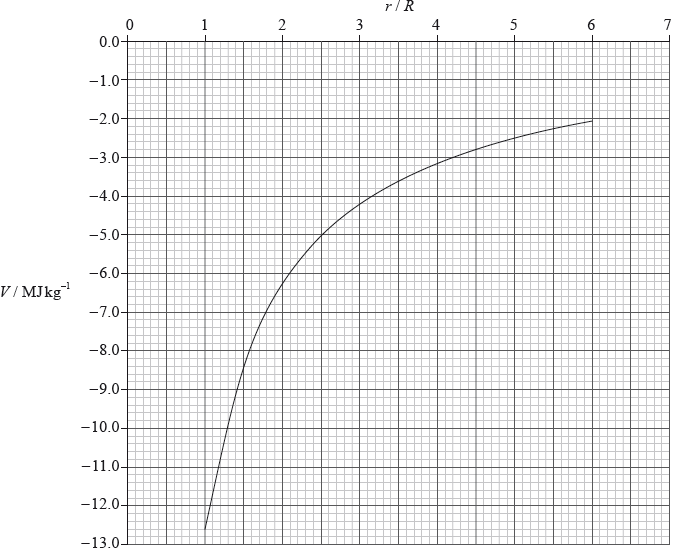
A rocket of mass \(1.2 \times {10^4}{\text{ kg}}\) lifts off from the surface of Mars. Use the graph to
(i) Ignoring air resistance, calculate the horizontal distance travelled by the clay block before it strikes the ground.
(ii) The diagram in (c) shows the path of the clay block neglecting air resistance. On the diagram, draw the approximate shape of the path that the clay block will take assuming that air resistance acts on the clay block.
Define gravitational potential energy of a mass at a point.
(i) calculate the change in gravitational potential energy of the rocket at a distance 4R from the centre of Mars.
(ii) show that the magnitude of the gravitational field strength at a distance 4R from the centre of Mars is \({\text{0.23 N}}\,{\text{k}}{{\text{g}}^{ - 1}}\).
The gravitational potential due to the Sun at its surface is –1.9 x 1011 J kg–1. The following data are available.
| Mass of Earth | = 6.0 x 1024 kg |
| Distance from Earth to Sun | = 1.5 x 1011 m |
| Radius of Sun | = 7.0 x 108 m |
Outline why the gravitational potential is negative.
The gravitational potential due to the Sun at a distance r from its centre is VS. Show that
rVS = constant.
Calculate the gravitational potential energy of the Earth in its orbit around the Sun. Give your answer to an appropriate number of significant figures.
Calculate the total energy of the Earth in its orbit.
An asteroid strikes the Earth and causes the orbital speed of the Earth to suddenly decrease. Suggest the ways in which the orbit of the Earth will change.
Outline, in terms of the force acting on it, why the Earth remains in a circular orbit around the Sun.
A planet has radius R. At a distance h above the surface of the planet the gravitational field strength is g and the gravitational potential is V.
State what is meant by gravitational field strength.
Show that V = –g(R + h).
Draw a graph, on the axes, to show the variation of the gravitational potential V of the planet with height h above the surface of the planet.
A planet has a radius of 3.1 × 106 m. At a point P a distance 2.4 × 107 m above the surface of the planet the gravitational field strength is 2.2 N kg–1. Calculate the gravitational potential at point P, include an appropriate unit for your answer.
The diagram shows the path of an asteroid as it moves past the planet.

When the asteroid was far away from the planet it had negligible speed. Estimate the speed of the asteroid at point P as defined in (b).
The mass of the asteroid is 6.2 × 1012 kg. Calculate the gravitational force experienced by the planet when the asteroid is at point P.
Hydrogen atoms in an ultraviolet (UV) lamp make transitions from the first excited state to the ground state. Photons are emitted and are incident on a photoelectric surface as shown.
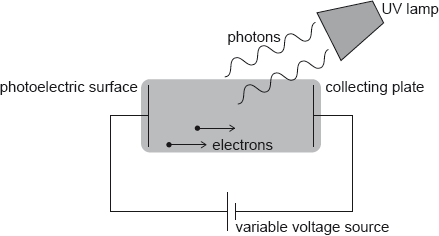
The photons cause the emission of electrons from the photoelectric surface. The work function of the photoelectric surface is 5.1 eV.
The electric potential of the photoelectric surface is 0 V. The variable voltage is adjusted so that the collecting plate is at –1.2 V.
Show that the energy of photons from the UV lamp is about 10 eV.
Calculate, in J, the maximum kinetic energy of the emitted electrons.
Suggest, with reference to conservation of energy, how the variable voltage source can be used to stop all emitted electrons from reaching the collecting plate.
The variable voltage can be adjusted so that no electrons reach the collecting plate. Write down the minimum value of the voltage for which no electrons reach the collecting plate.
On the diagram, draw and label the equipotential lines at –0.4 V and –0.8 V.
An electron is emitted from the photoelectric surface with kinetic energy 2.1 eV. Calculate the speed of the electron at the collecting plate.
Part 2 Motion of a rocket
A rocket is moving away from a planet within the gravitational field of the planet. When the rocket is at position P a distance of 1.30×107m from the centre of the planet, the engine is switched off. At P, the speed of the rocket is 4.38×103ms–1.
At a time of 60.0 s later, the rocket has reached position Q. The speed of the rocket at Q is 4.25×103ms–1. Air resistance is negligible.
Outline, with reference to the energy of the rocket, why the speed of the rocket is changing between P and Q.
Estimate the average gravitational field strength of the planet between P and Q.
(i) An object is a distance r from the centre of a planet. Show that the minimum speed required to escape the gravitational field is equal to
\[\sqrt {2g'r} \]
where g′ is the gravitational field strength at distance r from the centre of a planet.
(ii) Discuss, using a calculation, whether the rocket at P can completely escape the gravitational field of the planet without further use of the engine.
A space station is in orbit at a distance r from the centre of the planet in (e)(i). A satellite is launched from the space station so as just to escape from the gravitational field of the planet. The launch takes place in the same direction as the velocity of the space station. Outline why the launch velocity relative to the space station can be less than your answer to (e)(i).
There is a proposal to power a space satellite X as it orbits the Earth. In this model, X is connected by an electronically-conducting cable to another smaller satellite Y.
Satellite Y orbits closer to the centre of Earth than satellite X. Outline why
The cable acts as a spring. Satellite Y has a mass m of 3.5 x 102 kg. Under certain circumstances, satellite Y will perform simple harmonic motion (SHM) with a period T of 5.2 s.
Satellite X orbits 6600 km from the centre of the Earth.
Mass of the Earth = 6.0 x 1024 kg
Show that the orbital speed of satellite X is about 8 km s–1.
the orbital times for X and Y are different.
satellite Y requires a propulsion system.
The cable between the satellites cuts the magnetic field lines of the Earth at right angles.
Explain why satellite X becomes positively charged.
Satellite X must release ions into the space between the satellites. Explain why the current in the cable will become zero unless there is a method for transferring charge from X to Y.
The magnetic field strength of the Earth is 31 μT at the orbital radius of the satellites. The cable is 15 km in length. Calculate the emf induced in the cable.
Estimate the value of k in the following expression.
T = \(2\pi \sqrt {\frac{m}{k}} \)
Give an appropriate unit for your answer. Ignore the mass of the cable and any oscillation of satellite X.
Describe the energy changes in the satellite Y-cable system during one cycle of the oscillation.
This question is about the energy of an orbiting satellite.
A space shuttle of mass m is launched in the direction of the Earth’s South Pole.
The shuttle enters a circular orbit of radius \(R\) around the Earth.
The kinetic energy \({E_{\text{K}}}\) given to the shuttle at its launch is given by the expression
\[{E_{\text{K}}} = \frac{{7GMm}}{{8{R_{\text{E}}}}}\]
where \(G\) is the gravitational constant, \(M\) is mass of the Earth and \({R_{\text{E}}}\) is the radius of the Earth. Deduce that the shuttle cannot escape the gravitational field of the Earth.
Show that the total energy of the shuttle in its orbit is given by \( - \frac{{GMm}}{{2R}}\). Air resistance is negligible.
Using the expression for \({E_{\text{K}}}\) in (a) and your answer to (b)(i), determine \(R\) in terms of \({R_{\text{E}}}\).
In practice, the total energy of the shuttle decreases as it collides with air molecules in the upper atmosphere. Outline what happens to the speed of the shuttle when this occurs.
Outline what is meant by escape speed.
A probe is launched vertically upwards from the surface of a planet with a speed
\[v = \frac{3}{4}{v_{{\rm{esc}}}}\]
where vesc is the escape speed from the planet. The planet has no atmosphere.
Determine, in terms of the radius of the planet R, the maximum height from the surface of the planet reached by the probe.
The total energy of a probe in orbit around a planet of mass M is \(E = - \frac{{GMm}}{{2r}}\) where m is the mass of the probe and r is the orbit radius. A probe in low orbit experiences a small frictional force. Suggest the effect of this force on the speed of the probe.
This question is about escape speed and gravitational effects.
Explain what is meant by escape speed.
Titania is a moon that orbits the planet Uranus. The mass of Titania is 3.5×1021kg. The radius of Titania is 800 km.
(i) Use the data to calculate the gravitational potential at the surface of Titania.
(ii) Use your answer to (b)(i) to determine the escape speed for Titania.
An astronaut visiting Titania throws an object away from him with an initial horizontal velocity of 1.8 m s–1. The object is 1.5 m above the moon’s surface when it is thrown. The gravitational field strength at the surface of Titania is 0.37 N kg–1.
Calculate the distance from the astronaut at which the object first strikes the surface.
Explain what is meant by the gravitational potential at the surface of a planet.
An unpowered projectile is fired vertically upwards into deep space from the surface of planet Venus. Assume that the gravitational effects of the Sun and the other planets are negligible.
The following data are available.
| Mass of Venus | = 4.87×1024 kg |
| Radius of Venus | = 6.05×106 m |
| Mass of projectile | = 3.50×103 kg |
| Initial speed of projectile | = 1.10×escape speed |
(i) Determine the initial kinetic energy of the projectile.
(ii) Describe the subsequent motion of the projectile until it is effectively beyond the gravitational field of Venus.
This question is about a probe in orbit.
A probe of mass m is in a circular orbit of radius r around a spherical planet of mass M.
State why the work done by the gravitational force during one full revolution of the probe is zero.
Deduce for the probe in orbit that its
(i) speed is \(v = \sqrt {\frac{{GM}}{r}} \).
(ii) total energy is \(E = - \frac{{GMm}}{{2r}}\).
It is now required to place the probe in another circular orbit further away from the planet. To do this, the probe’s engines will be fired for a very short time.
State and explain whether the work done on the probe by the engines is positive, negative or zero.
This question is about electric potential.
Define electric potential at a point in an electric field.
A positive point charge is moving towards a small, charged metal sphere along a radial path.
At the position shown in the diagram, the point charge has a speed of 3.50 m s–1 and is at a distance of 2.78 m from the centre of the metal sphere. The charge on the sphere is +4.00 μC.
(i) State the direction of the velocity of the point charge with respect to an equipotential surface due to the metal sphere.
(ii) Show that the electric potential V due to the charged sphere at a distance of 2.78 m from its centre is 1.29 ×104 V.
(iii) The electric potential at the surface of the sphere is 7.20 ×104 V. The point charge has a charge of +0.0320 μC and its mass is 1.20 ×10– 4 kg. Determine if the point charge will collide with the metal sphere.
This question is in two parts. Part 1 is about electric charge and resistance. Part 2 is about orbital motion.
Part 1 Electric charge and resistance
Two plastic rods each have a positive charge +q situated at one end. The rods are arranged as shown.
Assume that the charge at the end of each rod behaves as a point charge. Draw, in the shaded area on the diagram
(i) the electric field pattern due to the two charges.
(ii) a line to represent an equipotential surface. Label the line with the letter V.
Part 2 Gravitational potential
Define gravitational potential at a point in a gravitational field.
The graph shows how the gravitational potential V of Earth varies with distance R from the centre of Earth in the range R=2.0×108 m to R=5.0×108 m.
The Moon is at a distance of 4.0×108 m from the centre of Earth. At some time in the past it was at a distance of 2.7×108 m from the centre of Earth.
Use the graph opposite to determine
(i) the present day magnitude of the acceleration of the Moon.
(ii) by how much the potential energy of the Moon has changed as a result of moving from R=2.7×108 m to R=4.0×108 m. The mass of the Moon is 7.4×1022 kg.
State why the change of potential energy in (f)(ii) is an increase.
Part 2 Orbital motion
A satellite, of mass m, is in orbit about Earth at a distance r from the centre of Earth. Deduce that the kinetic energy EK of the satellite is equal to half the magnitude of the potential energy EP of the satellite.
The graph shows the variation with distance r of the Earth’s gravitational potential V. Values of V for r<R, where R is the radius of Earth, are not shown.
The satellite in (a) has a mass of 8.2×102kg and it is in orbit at a distance of 1.0×107m from the centre of Earth. Using data from the graph and your answer to (a), calculate for the satellite
(i) its total energy.
(ii) its orbital speed.
(iii) the energy it must gain to move to an orbit a distance 2.0×107 m from the centre of the Earth.
This question is in two parts. Part 1 is about solar radiation and the greenhouse effect. Part 2 is about orbital motion.
Part 1 Solar radiation and the greenhouse effect
The following data are available.
Part 2 Orbital motion
A spaceship of mass m is moving at speed v in a circular orbit of radius r around a planet of mass M.
State the Stefan-Boltzmann law for a black body.
Deduce that the solar power incident per unit area at distance d from the Sun is given by
\(\frac{{\sigma {R^2}{T^4}}}{{{d^2}}}\).
Calculate, using the data given, the solar power incident per unit area at distance d from the Sun.
State two reasons why the solar power incident per unit area at a point on the surface of the Earth is likely to be different from your answer in (c).
The average power absorbed per unit area at the Earth’s surface is 240Wm–2. By treating the Earth’s surface as a black body, show that the average surface temperature of the Earth is approximately 250K.
Explain why the actual surface temperature of the Earth is greater than the value in (e).
(i) Identify the force that causes the centripetal acceleration of the spaceship.
(ii) Explain why astronauts inside the spaceship would feel “weightless”, even though there is a force acting on them.
Deduce that the speed of the spaceship is \(v = \sqrt {\frac{{GM}}{r}} \).
The table gives equations for the forms of energy of the orbiting spaceship.
The spaceship passes through a cloud of gas, so that a small frictional force acts on the spaceship.
(i) State and explain the effect that this force has on the total energy of the spaceship.
(ii) Outline the effect that this force has on the speed of the spaceship.
The diagram shows the gravitational field lines of planet X.
Outline how this diagram shows that the gravitational field strength of planet X decreases with distance from the surface.
The diagram shows part of the surface of planet X. The gravitational potential at the surface of planet X is –3V and the gravitational potential at point Y is –V.
Sketch on the grid the equipotential surface corresponding to a gravitational potential of –2V.
A meteorite, very far from planet X begins to fall to the surface with a negligibly small initial speed. The mass of planet X is 3.1 × 1021 kg and its radius is 1.2 × 106 m. The planet has no atmosphere. Calculate the speed at which the meteorite will hit the surface.
At the instant of impact the meteorite which is made of ice has a temperature of 0 °C. Assume that all the kinetic energy at impact gets transferred into internal energy in the meteorite. Calculate the percentage of the meteorite’s mass that melts. The specific latent heat of fusion of ice is 3.3 × 105 J kg–1.