
HL Paper 3
A positive pion decays into a positive muon and a neutrino.
\[{\pi ^ + } \to {\mu ^ + } + {v_\mu }\]
The momentum of the muon is measured to be 29.8 MeV c–1 in a laboratory reference frame in which the pion is at rest. The rest mass of the muon is 105.7 MeV c–2 and the mass of the neutrino can be assumed to be zero.
For the laboratory reference frame
write down the momentum of the neutrino.
show that the energy of the pion is about 140 MeV.
State the rest mass of the pion with an appropriate unit.
Markscheme
«–»29.8 «MeVc–1»
[1 mark]
Eπ = \(\sqrt {p_\mu ^2{c^2} + m_\mu ^2{c^4}} \) + pvc OR Eμ = 109.8 «MeV»
Eπ = «\(\sqrt {{{29.8}^2} + {{105.7}^2}} \) + 29.8 =» 139.6 «MeV»
Final value to at least 3 sig figs required for mark.
[2 marks]
139.6 MeVc–2
Units required.
Accept 140 MeVc–2.
[1 mark]
Examiners report
This question is about interactions and quarks.
For the lambda baryon \({\Lambda ^0}\), a student proposes a possible decay of \({\Lambda ^0}\) as shown.
\[{\Lambda ^0} \to p + {K^ - }\]
The quark content of the \({K^ - }\) meson is \({\rm{\bar us}}\).
A lambda baryon \({\Lambda ^0}\) is composed of the three quarks uds. Show that the charge is 0 and the strangeness is \( - 1\).
Discuss, with reference to strangeness and baryon number, why this proposal is feasible.
Strangeness:
Baryon number:
Another interaction is
\[{\Lambda ^0} \to p + {\pi ^ - }.\]
In this interaction strangeness is found not to be conserved. Deduce the nature of this interaction.
Markscheme
\( + \frac{2}{3} - \frac{1}{3} - \frac{1}{3} = 0\) for charge;
any particle containing a strange quark has strangeness of \( - 1\);
strangeness:
the \(p\) has a strangeness of 0;
the \({K^ - }\) particle has a strangeness of \( - 1\);
baryon number:
lambda and protons are baryons each having a baryon number of \( + 1\);
the \({K^ - }\) meson has a baryon number of 0;
only during the weak interaction strangeness is not conserved (therefore it is a weak interaction);
Examiners report
Well answered question, often very clearly and straightforward; some, even better candidates made mistakes in calculation in (b)(iii).
Well answered question, often very clearly and straightforward; some, even better candidates made mistakes in calculation in (b)(iii).
Well answered question, often very clearly and straightforward; some, even better candidates made mistakes in calculation in (b)(iii).
This question is about particle interactions.
An electron and a positron interact to produce a muon and antimuon through a weak interaction. The weak interaction involves one of the virtual particles \({{\text{W}}^ - }\), \({{\text{W}}^ + }\) or \({{\text{Z}}^{\text{0}}}\) boson.
Describe what is meant by a virtual particle.
Draw a Feynman diagram which represents this interaction.
Explain whether this interaction involves the \({{\text{W}}^ - }\), \({{\text{W}}^ + }\) or \({{\text{Z}}^{\text{0}}}\) boson.
Markscheme
a particle that mediates one of fundamental forces / a particle that appears as an intermediate particle in a Feynman diagram / a particle that is not observed and may violate energy and momentum conservation at a vertex;
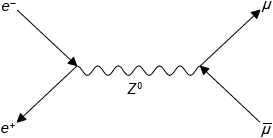
electron and positron directions and symbols shown correctly;
muon and antimuon directions and symbols shown correctly;
\({{\text{Z}}^0}\) boson, no charge has been transferred/neutral current;
Examiners report
Generally well answered.
Generally well answered.
Generally well answered.
This question is about particles and interactions.
When a free neutron decays to a proton, an electron is one of the decay products.
(i) State the name of the exchange particle and the interaction involved in this decay.
(ii) The interaction and the exchange particle in (a)(i) may arise when a quark decays. Describe the change in the quark structure of the neutron.
Markscheme
(i) W/intermediate vector boson and weak; (both needed for mark)
(ii) d in neutron changes to u (in proton);
Examiners report
This question is about a K meson decay.
The positive kaon K+ has a strangeness of +1. It can decay through the interaction
K+ → μ+ + νμ.
Charge, energy and momentum are conserved in this decay.
State the quark structure of the K+.
Deduce one further quantity in this decay that is
(i) conserved.
(ii) not conserved.
Markscheme
\(u\overline s \);
(i) baryon/lepton number / colour;
(ii) strangeness;
Examiners report
This question is about the standard model.
State what is meant by the standard model.
Use the conservation of lepton number and charge to deduce the nature of the particle x in the following reaction.
\[{v_{\text{e}}} + {\mu ^ - } \to {e^ - } + x\]
State what is meant by deep inelastic scattering.
Markscheme
the theory that describes the electromagnetic and weak (and strong) interaction of quarks and electrons/particles;
\({v_\mu }\) / muon neutrino;
scattering (of leptons by hadrons) in which large amounts of energy is transferred (to the hadrons);
Examiners report
A significant number of candidates left the question unanswered. Of those candidates who did attempt the question very few knew anything about deep inelastic scattering.
A significant number of candidates left the question unanswered. Of those candidates who did attempt the question very few knew anything about deep inelastic scattering.
A significant number of candidates left the question unanswered. Of those candidates who did attempt the question very few knew anything about deep inelastic scattering.
This question is about particle production.
In a particular experiment, moving kaon mesons collide with stationary protons. The following reaction takes place
\[p + {K^ - } \to {K^0} + {K^ + } + X\]
where X is an unknown particle. This process involves the strong interaction. The quark structure of the kaons is \({K^ - } = \bar us\), \({K^0} = d\bar s\), and \({K^ + } = \bar us\).
(i) State the strangeness of the unknown particle X.
(ii) Particle X is a hadron. State and explain whether X is a meson or a baryon.
Markscheme
(i) S = -3;
(ii) baryon;
to conserve baryon number / has structure sss;
Examiners report
(a)(i) a strangeness = -3 was usually correctly given, as was the identification of X as a baryon.
This question is about elementary particles.
The quark is said to be an elementary particle.
(i) State what is meant by the term elementary particle.
(ii) Identify another elementary particle other than the quark.
Markscheme
(i) particle with no internal structure / cannot be broken down further;
(ii) Electron / neutrino / any lepton / any named exchange particle;
Examiners report
Well answered although many answers just said “lepton” in (ii) without naming it.
This question is about linear accelerators.
A moving proton is incident on a stationary pion, producing a kaon (K meson) and an unknown hadron X according to the reaction given below.
p+π−→X+K−
(i) State, with a reason, the electric charge of X.
(ii) State, with a reason, if X is a baryon or a meson.
In a deep inelastic scattering experiment, protons of momentum 2.70 ×10–18 N s are scattered by gold nuclei.
Given that the diameter of nucleons is of the order 10–15 m and the diameter of quarks is less than 10–18 m, determine if these protons will be able to resolve
(i) nucleons within the gold nuclei.
(ii) quarks within the gold nuclei.
Outline how deep inelastic scattering experiments led to the conclusion that gluons exist.
Markscheme
(i) positive in order to satisfy electric charge conservation;
(ii) baryon in order to satisfy baryon number conservation/contains 3 quarks;
(i) the de Broglie wavelength is \(\lambda = \frac{{6.63 \times {{10}^{ - 34}}}}{{2.7 \times {{10}^{ - 18}}}} = 2.5 \times {10^{ - 16}}{\rm{m}}\);
this is less than the nucleon size so nucleons can be resolved;
Argument required for second mark.
(ii) but it is greater than the quark size so quarks cannot be resolved;
deep inelastic scattering experiments measure the (fraction of) momentum carried by electrically charged constituents of hadrons;
this is less than the total momentum of the hadron indicating the presence of neutral constituents;
Examiners report
This question is about deep inelastic scattering.
A student states that “the strong nuclear force is the strongest of the four fundamental interactions”. Explain why this statement is not correct.
Describe how deep inelastic scattering experiments support your answer to (a).
State two other conclusions that may be reached from deep inelastic scattering experiments.
Markscheme
the statement is true only for low energies;
at higher energies the strength of the strong interaction decreases;
in deep inelastic scattering experiments the energy transferred to the constituents of hadrons is very large;
the scattering pattern is consistent with quarks inside hadrons behaving as free particles / the interaction between the constituents is very weak (asymptotic freedom);
there are electrically neutral constituents inside hadrons / there are gluons within hadrons;
quarks come in (three) colours;
quarks are charged particles;
Examiners report
This question is about conservation laws and the standard model.
A muon decays into an electron and two other particles according to the reaction equation μ−→e−+?+?.
State the names of the two other particles that are produced in this decay explaining your answer.
Markscheme
muon neutrino;
electron antineutrino;
so that (family) lepton number is conserved;
Do not accept particle symbols only.
Examiners report
This question is about the standard model.
The Feynman diagrams show two electroweak interactions between electrons. The particle represented by the wavy line is a photon.
State
(i) the name of the exchange particle represented by the dotted line.
(ii) one difference between the two exchange particles.
Outline how the observation of the interaction represented by the diagram with the dotted line provides evidence for the standard model.
Markscheme
(i) Z (boson) / Z0 / boson;
(ii) Z is massive/has mass;
neutral current interaction (mentioned);
which is only observed with a weak/electroweak (interaction);
as predicted by the standard model;
Examiners report
This was generally well answered by well prepared candidates. Many identified the Z boson in (a)(i).
In (b), incorrect answers were rare. Candidates with sound knowledge answered well and others did not answer at all.
This question is about quarks.
State the name of a particle that is its own antiparticle.
The meson K0 consists of a d quark and an anti s quark. The K0 decays into two pions as shown in the Feynman diagram.
(i) State a reason why the kaon K0 cannot be its own antiparticle.
(ii) Explain how it may be deduced that this decay is a weak interaction process.
(iii) State the name of the particle denoted by the dotted line in the diagram.
(iv) The mass of the particle in (b)(iii) is approximately 1.6×10–25kg. Determine the range of the weak interaction.
Markscheme
photon / graviton / Z / Higgs;
(i) K0 has a strangeness of +1, its antiparticle has strangeness –1 and so are different;
the antiparticle is s, \(\overline d \) and so is different;
(ii) strangeness is violated in this decay;
this can only happen with the weak interaction;
(iii) Z0 / Z;
(iv) \(R = \left( {\frac{h}{{4\pi mc}} = } \right)\frac{{6.6 \times {{10}^{ - 34}}}}{{4 \times \pi \times 1.6 \times {{10}^{ - 25}} \times 3.0 \times {{10}^8}}}\);
R≈10−18m;
Award [2] for a bald correct answer.
Examiners report
This question is about hadrons.
The interaction in (a) can also occur via the weak interaction with neutral current mediation producing an up and anti-up quark pair.
Draw a labelled Feynman diagram for this interaction. Time on your diagram should go from left to right.
Markscheme
correct incoming and outgoing particles with correct arrow direction;
Z0 shown correctly;
Allow any consistent labelling for quark pair.
Examiners report
Were reasonably well answered
This question is about the early universe and the Higgs boson.
The graph shows the variation of the logarithm of the temperature T of the universe with the logarithm of the time t after the Big Bang.
Evidence for the Higgs boson might be discovered at the Large Hadron Collider (LHC) at CERN. Outline why such a discovery would be of crucial significance to the standard model.
Markscheme
the Higgs is the only undiscovered particle of the standard model;
the discovery would help to verify standard model / failure to discover it would necessitate a change in the model;
the Higgs is responsible for giving mass to particles / is linked to the problem of mass so its discovery would shed light on the problem of mass;
Examiners report
This question is about particles and interactions.
(i) State what is meant by an antiparticle.
(ii) Some particles are identical to their antiparticles. Discuss whether the neutron and the antineutron are identical.
The Feynman diagram represents the decay \({K^{\rm{ - }}} \to {\pi ^{\rm{ + }}}{\rm{ + }}{\pi ^{\rm{ - }}}{\rm{ + }}{\pi ^{\rm{ - }}}\).
Particles X and Y are exchange particles.
(i) Explain what is meant by an exchange particle.
(ii) Identify X.
(iii) Determine the electric charge of Y.
(iv) Calculate the change in strangeness in the decay of the K –.
Markscheme
(i) a particle with the same mass but opposite quantum numbers/charge;
(ii) the neutron has baryon number +1, so the antineutron has baryon number -1
so they are different;
or
the neutron consists of three quarks (udd) and the antineutron consists of three antiquarks \(\left( {{\rm{\bar u\bar d\bar d}}} \right)\);
so they are different;
Award [0] for a bald correct answer.
(i) a short lived/virtual particle/(gauge) boson;
that transfers energy/momentum/force between interacting particles;
(ii) W–;
(iii) zero;
(iv) \(\Delta S = 0 - \left( { - 1} \right) = + 1\)
Examiners report
In (a)(i) the fact that antiparticles have equal mass was often not mentioned. Most realised that antineutrons and neutrons were not identical as they had different quark structure or opposite baryon numbers.
Part (b)(i) was usually partially correct. Few mentioned that exchange particles were bosons. Parts (ii), (iii) and (iv) were answered correctly only if candidates knew the charges on the various quarks in the Feynman diagram. About half did know.
This question is about the standard model and the Pauli exclusion principle.
State one conservation law that would be violated, if the following reactions were to occur.
(i) \({\pi ^0} \to {e^ + } + {\mu ^ - }\)
(ii) \({p^ + } + \bar n \to {e^ + } + {e^ - } + {\bar v_e} + {v_e}\)
The reaction \({\bar v_\mu } + {e^ - } \to {\bar v_\mu } + {e^ - }\) is an example of a neutral current reaction. Draw a Feynman diagram for this reaction labelling all the particles involved. The arrow provided indicates the direction of time.
Markscheme
(i) electron lepton number/muon lepton number/family lepton number;
Do not accept just “lepton number” as this is conserved.
(ii) electric charge;
arrows for e– point forward in time and arrows for \({\bar v_\mu }\) point backwards in time;
vertices \({\bar v_\mu }Z{\bar v_\mu }\) and e–Ze– ; (inspect carefully, many draw \({e^ - }Z{\bar v_\mu }\) vertices)
Z particle;
Award each marking point independently.
Award [2 max] if the diagram is rotated 90º.
Allow particles to be expressed in words.
Examiners report
Part (a)(i) was poorly answered as many just stated lepton number is not conserved. They needed to be specific. In (ii) a common mistake was to think that baryon number is not conserved when in fact it is charge that is not conserved.
The Feynman diagram in (b) was rarely correct. Far too many candidates drew vertices that did not conserve charge. However partial marks were obtained for identifying the Z boson or for correct arrow directions.
This question is about the standard model.
Muons can decay via the weak interaction into electrons and neutrinos. One such decay is
\[{\mu ^ + } \to {e^ + } + {v_e} + {\bar v_\mu }\]
(i) Using the table provided, show that in this decay, lepton number L, electron lepton number Le and muon lepton number Lμ are all conserved.
(ii) Label the Feynman diagram below for the decay of a positive muon (μ+).