
SL Paper 3
This question is about the Doppler effect.
Georgia carries out an experiment to measure the speed of mosquitoes. She sets up a microphone to record the sounds of passing mosquitoes.

One mosquito is moving in a straight line with constant speed and passes very close to the microphone as seen in the diagram. The mosquito produces a sound of constant frequency.
The speed of sound in air is \({\text{340 m}}\,{{\text{s}}^{ - {\text{1}}}}\).
The maximum frequency recorded is 751 Hz and the minimum frequency recorded is 749 Hz. Explain this observation.
Determine the speed of the mosquito.
Markscheme
as the mosquito approaches the wavelength perceived by Georgia is shorter and therefore the perceived frequency is higher;
as the mosquito is moving away, the wavelength perceived is longer than the emitted and therefore the perceived frequency is lower;
due to the Doppler effect;
approaching \(751 = f \times \frac{{340}}{{340 - u}}\);
moving away \(749 = f \times \frac{{340}}{{340 + u}}\);
to produce \(u = 0.45{\text{ m}}\,{{\text{s}}^{ - 1}}\);
or
emitted frequency is \(\frac{{751 + 749}}{2} = 750{\text{ Hz}}\);
applying the Doppler effect for approach (or recession), \(751 = 750\frac{{340}}{{340 - u}}\)\(\,\,\,\)or\(\,\,\,\)\(749 = 750\frac{{340}}{{340 + u}}\);
to produce \(u = 0.45{\text{ m}}\,{{\text{s}}^{ - 1}}\);
Examiners report
In (a), many candidates drew the classic diagram with wavefronts closer in front of the source and further apart behind. However, very few related this to the situation and the values given.
(b) was a more difficult question with few working through to the solution.
This question is about the Doppler effect.
A child on a carousel (merry-go-round) moves with a speed of \({\text{6.5 m}}\,{{\text{s}}^{ - 1}}\) along a horizontal circular path ABCDA. A stationary observer is at a large distance from the carousel.
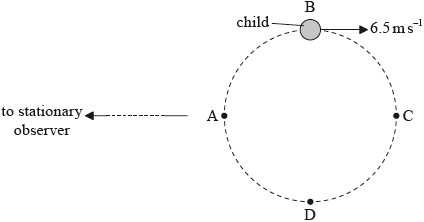
The child blows a whistle while moving from position B to position D. The whistle emits sound of frequency 850 Hz. The speed of sound in air is \({\text{330 m}}\,{{\text{s}}^{ - 1}}\).
Describe what is meant by the Doppler effect.
(i) Determine the minimum frequency of the sound heard by the observer.
(ii) Describe the variation of the frequency of the sound heard by the observer.
Markscheme
change in the observed/perceived frequency;
when there is relative motion between the source and the observer / when either the source or observer is moving;
(i) \(f = 850\left[ {\frac{{330}}{{330 + 6.5}}} \right]\);
\(f = 830{\text{ (Hz)}}\);
Award [1 max] for correct answer if moving observer equation is used with 6.5 in the numerator or if the approximate formula is used.
(ii) frequency increases;
(from 830 (Hz)) to 870 (Hz);
Examiners report
(a) was usually answered correctly, but it is worth emphasising that it is the perceived frequency that changes.
In (i) there were many correct answers, but sometimes the wrong Doppler equation was used or an incorrect sign convention chosen. Having found the minimum frequency (at position B) the vast majority then stated, in (ii), that frequency decreased from B to C. This is a question that needs careful discussion in class with future candidates.
This question is about interference.
Light from a laser is incident on two identical parallel slits. The light from the two slits produces a fringe pattern on a screen.

A central bright fringe is produced at C. The next bright fringe is produced at A. There is a dark fringe at B.
The light from the laser is coherent and monochromatic.
The distance from the two slits to the screen is 1.5 m. The distance BC is 1.8 mm and the distance between the slits is 0.30 mm.
Outline what is meant by the term
(i) coherent.
(ii) monochromatic.
State the phase difference between the light waves from the two slits that meet at B.
(i) Show that the laser produces light of wavelength equal to 720 nm.
(ii) State the path difference, in metres, between the waves that meet at B.
Determine the number of lines per metre of the diffraction grating.
Markscheme
(i) constant/zero phase difference (between the light waves);
(ii) single/same wavelength/frequency; (allow “narrow band” OWTTE)
Do not allow “single colour”.
\(180^\circ /\pi {\text{rad}}\);
Do not accept \(\frac{\lambda }{2}\).
(i) use of \(\lambda = \frac{{sd}}{D}\);
\(s = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{2} \times 1.8{\text{ (mm)}}\); (award this mark for any evidence for the factor of 2)
\(\lambda = \frac{{{\text{2}} \times {\text{1.8}} \times {\text{1}}{{\text{0}}^{ - 3}} \times {\text{0.30}} \times {\text{1}}{{\text{0}}^{ - 3}}}}{{{\text{1.5}}}}\) / OWTTE;
\({\text{(}} = 7.2 \times {10^{ - 7}}{\text{ m)}}\)
Exact answer is given, award marks for correct working.
(ii) \({\text{3.6}} \times {\text{1}}{{\text{0}}^{ - 7}}{\text{ m}}\)\(\,\,\,\)or\(\,\,\,\)360 nm;
Allow ECF from (c)(i).
use of \(d = \frac{{n\lambda }}{{\sin \theta }}\);
\(d = \frac{{3 \times 720 \times {{10}^{ - 9}}}}{{\sin 39^\circ }} = 3.4 \times {10^{ - 6}}{\text{ (m)}}\);
\(N = \left( {\frac{1}{{3.4 \times {{10}^{ - 6}}}} = } \right){\text{ }}2.9 \times {10^5}\);
Award [3] for a bald correct answer.
ECF examples:
Award [2 max] if n = 2 is used (gives 4.4 \( \times \) 105).
Award [2 max] if 78° is used (gives 4.5 \( \times \) 105).
Award [2 max] if 13° and n = 1 used (gives 3.1 \( \times \) 105).
Examiners report
This question is about diffraction and resolution.
A parallel beam of monochromatic light is incident on a narrow rectangular slit. After passing through the slit, the light is incident on a distant screen.
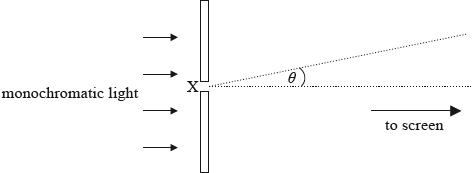
Point X is the midpoint of the slit.
(i) On the axes below, sketch a graph to show how the intensity of the light on the screen varies with the angle \(\theta \) shown in the diagram.
(ii) The wavelength of the light is 520 nm, the width of the slit is 0.04 mm and the screen is 1.2 m from the slit. Show that the width of the central maximum of intensity on the screen is about 3 cm.
Points P and Q are on the circumference of a planet as shown.
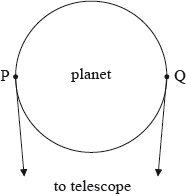
By considering the two points, outline why diffraction limits the ability of an astronomical telescope to resolve the image of the planet as a disc.
Markscheme
(i) 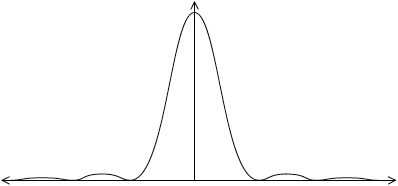
general correct shape touching axis and symmetric about \(\theta = 0\) (at least onesecondary maxima on each side); (judge by eye)
central maximum wider than secondary maxima;
secondary maxima at most one third intensity of central maximum;
(ii) \(\frac{d}{2} = \frac{{D\lambda }}{b}\);
\(d = \frac{{2.0 \times 1.2 \times 5.2 \times {{10}^{ - 7}}}}{{4.0 \times {{10}^{ - 5}}}} = 3.12 \times {10^{ - 2}}{\text{ m}}\);
\( \approx 3{\text{ cm}}\)
Award [2 max] for a sensible argument.
e.g. light from each point forms a diffraction pattern after being focussed by the eyepiece of the telescope;
if the diffraction patterns are not sufficiently well separated then the points will not be resolved as separate sources;
Award [1 max] for the conclusion.
e.g. if the points cannot be resolved as separate sources the planet cannot be seen as a disc;
Examiners report
Intensity distributions were often drawn well but quite a few candidates did not have their graphs in contact with the \(\theta \) axis. Candidates’ working was often difficult to follow in the calculation part of this question.
Very few candidates recognised the role played by diffraction in the resolution of the planet as a disc.
This question is about a diffraction grating.
For a particular grating, the distance between adjacent slits is \(2.0 \times {10^{ - 6}}{\text{ m}}\). Determine, for light of wavelength 520 nm, the maximum theoretical order of diffraction.
Markscheme
\(n = \left( {\frac{d}{\lambda } = } \right){\text{ }}\left( {\frac{{2.0 \times {{10}^{ - 6}}}}{{5.2 \times {{10}^{ - 7}}}} = } \right){\text{ 3.85}}\);
so \(\max = 3\);
Examiners report
The application of the formula in part (b) was often done well.
This question is about the Doppler effect.
Describe what is meant by the Doppler effect as it relates to sound.
An ambulance is travelling at a speed of 28.0 ms–1 along a straight road. Its siren emits a continuous sound of frequency 520 Hz. The ambulance is approaching a stationary observer. The observer measures the frequency of the note to be 566 Hz. Determine the speed of sound.
Markscheme
observed/perceived change in pitch/frequency;
when there is relative motion between source and observer;
recognize that \(f' = \left[ {\frac{v}{{v - {u_{\rm{s}}}}}} \right]f\);
\(566 = \left[ {\frac{v}{{v - 28}}} \right]520\);
to give v=345(ms-1) ;
Award [0] for use of the moving observer Doppler equation.
Award [2 max] for the use of +28 to give -345(ms-1).
Otherwise award only the first marking point for substitution of the incorrect values in the correct equation.
Examiners report
This question is about radio telescopes.
A distant galaxy emits radio waves of frequency 6.0×109 Hz and is moving with speed 6.0×106 ms–1 directly away from an observer on Earth.
Determine the wavelength of the radio wave as measured by the observer on Earth.
The radio signals from two stars on opposite sides of the galaxy are detected on Earth using a radio telescope. The telescope has a circular receiving dish.
(i) State the Rayleigh criterion for the images of two point sources to be just resolved.
(ii) The galaxy is 2.0×1021m from Earth and the stars are separated by 5.0×1019m. Determine the minimum size of the telescope dish required to resolve the images of the two stars at a wavelength of 5.1×10–2m.
Markscheme
\(\left( {{\rm{since}}\frac{v}{c} \ll 1} \right)\)\(\Delta f\left( { = \frac{v}{c}f} \right) = \frac{{6.0 \times {{10}^6}}}{{3.0 \times {{10}^8}}}6.0 \times {10^9}\left( { = 0.12 \times {{10}^9}{\rm{Hz}}} \right)\);
\(f' = f - \Delta f\left( { = 5.9 \times {{10}^9}{\rm{Hz}}} \right)\);
\(\lambda '\left( { = \frac{c}{{f'}} = \frac{{3.00 \times {{10}^8}}}{{5.9 \times {{10}^9}}}} \right) = 5.1 \times {10^{ - 2}}\left( {\rm{m}} \right)\);
Award [2 max] if ƒ'=ƒ+Δƒ used to give λ'=4.9x10-2(m).
(i) the two (point-like) sources generate diffraction patterns with central maxima;
the central maximum of one pattern overlaps with the first minimum of the second diffraction pattern;
(ii) \(\theta \approx \frac{d}{D} = \frac{{5.0 \times {{10}^{19}}}}{{2.0 \times {{10}^{21}}}} = 0.025({\rm{rad}})\)
\(\left( {b > 1.22\frac{{5.1 \times {{10}^{ - 2}}}}{{0.025}} = } \right)2.5\left( {\rm{m}} \right)\);
Allow [1 max] for solution that omits 1.22.
Examiners report
was well done by some, although many used the equation appropriate for sound not the approximation for light where c >> v.
In (b) (i) candidates often got the first mark by implication when gaining second mark. There was a lot of confused algebra in (b)(ii).
This question is about resolution and polarization.
A ship sails towards two stone towers built on land.
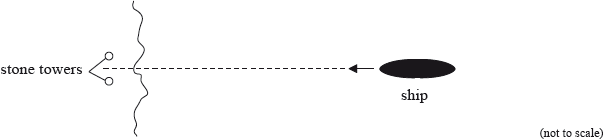
Emlyn, who is on the ship, views the towers. The pupils of Emlyn’s eyes are each of diameter 2.0 mm. The average wavelength of the sunlight is 550 nm.
State the Rayleigh criterion.
(i) Calculate the angular separation of the two towers when the images of the towers are just resolved by Emlyn.
(ii) Emlyn can just resolve the images of the two towers when his distance from the towers is 11 km. Determine the distance between the two towers.
Emlyn puts on a pair of polarizing sunglasses. Explain how these sunglasses reduce the intensity of the light, reflected from the sea, that enters Emlyn’s eyes.
Markscheme
for the images (of two sources) just to be resolved/distinguished/seen as separate;
central maximum of one diffraction pattern must coincide with first minimum of second / OWTTE;
Accept a suitably drawn diagram for the second marking point.
(i) \(\theta = \left( {\frac{{{\text{1.22}} \times {\text{550}} \times {\text{1}}{{\text{0}}^{ - 9}}}}{{{\text{2.0}} \times {\text{1}}{{\text{0}}^{ - 3}}}} = } \right){\text{ }}3.4 \times {10^{ - 4}}{\text{ (rad)}}\)\(\,\,\,\)or\(\,\,\,\)0.019°;
(ii) \(d = 11 \times {10^3} \times 3.4 \times {10^{ - 4}}\);
\( = {\text{3.7 (m)}}\);
Award [2] for a bald correct answer.
reflected light is (partially) polarized parallel to sea surface/horizontally polarized;
sunglasses have a transmission axis at 90° to reflected light/vertical transmission axis;
Examiners report
An improvement in the answers to (a) was noted.
In (b) very few omitted to use the factor of 1.22 and full marks were often scored for both calculations.
(d) was poorly answered with many being unable to make it clear that reflected light from the sea would be partially horizontally polarized. Some just referred to the darkness of the sunglasses' lens.
This question is about the Doppler effect.
The sound emitted by a car’s horn has frequency ƒ , as measured by the driver. An observer moves towards the stationary car at constant speed and measures the frequency of the sound to be ƒ '.
Explain, using a diagram, any difference between ƒ and ƒ'.
The frequency ƒ is 3.00×102Hz. An observer moves towards the stationary car at a constant speed of 15.0ms−1. Calculate the observed frequency ƒ' of the sound. The speed of sound in air is 3.30×102ms−1.
Markscheme
circular wavefronts around source, equally spaced;
moving observer intercepts more wavefronts per unit time / the time between intercepting successive wavefronts is less;
hence observes a higher frequency / ƒ′ > ƒ;
or
circular wavefronts around source, equally spaced;
the velocity of the sound waves with respect to the observer is greater;
since \(f' = \frac{{v'}}{\lambda }\), observed frequency is also greater;
\(f' = f\left( {\frac{{v + {u_o}}}{v}} \right) = 300\left( {\frac{{330 + 15}}{{330}}} \right)\);
=314 Hz;
Award [0] for use of moving source formula.
Award [1] for use of v-uo to give 286 Hz.
Examiners report
This question is about using a diffraction grating to view the emission spectrum of sodium.
Light from a sodium discharge tube is incident normally upon a diffraction grating having 8.00×105 lines per metre. The spectrum contains a double yellow line of wavelengths 589 nm and 590 nm.
Determine the angular separation of the two lines when viewed in the second order spectrum.
State why it is more difficult to observe the double yellow line when viewed in the first order spectrum.
Markscheme
\(d = \frac{1}{{8.00 \times {{10}^5}}} = 1.25 \times {10^{ - 6}}{\rm{m}}\);
\(d\sin \theta = n\lambda \Rightarrow \theta {\sin ^{ - 1}}\left[ {\frac{{n\lambda }}{d}} \right]\);
\({\sin ^{ - 1}}\left[ {\frac{{2 \times 589 \times {{10}^{ - 9}}}}{{1.25 \times {{10}^{ - 6}}}}} \right] = {\rm{ }}70.5^\circ {\rm{ }},{\sin ^{ - 1}}\left[ {\frac{{2 \times 590 \times {{10}^{ - 9}}}}{{1.25 \times {{10}^{ - 6}}}}} \right] = 70.7^\circ \);
70.7°−70.5°=0.2°;
the lines are closer together / not clearly separate in the first order spectrum;
Examiners report
This question is about the Doppler effect.
Describe the Doppler effect.
A spectral line from a source on Earth has a frequency of 4.672×1014 Hz. When this same line is observed from a distant galaxy it is found to have shifted to 4.669×1014 Hz.
(i) State the direction of the motion of the galaxy relative to Earth.
(ii) Deduce the speed of the galaxy relative to Earth.
Markscheme
(apparent) shift in frequency of wave;
when relative motion between source of waves and observer;
approach gives increase in frequency / recession decrease in frequency;
Allow answer in terms of red or blue shifts.
(i) galaxy moving away from Earth;
(ii) rearranges data book equation thus \(v \approx \frac{{\Delta f}}{f}c\);
\(v = \frac{{3.0 \times {{10}^{11}} \times 3 \times {{10}^8}}}{{4.672 \times {{10}^{14}}}}\);
\(v = 1.93 \times {10^5}{\rm{m}}{{\rm{s}}^{ - 1}}\);
Examiners report
This question is about diffraction and resolution.
Monochromatic light is incident normally on a single narrow slit and gives rise to a diffraction pattern on a screen.
Sketch, for the diffraction pattern produced, a graph showing the variation of the relative intensity of the light with the angle measured from the centre of the slit.
The single narrow slit is replaced by a double narrow slit. Explain, with reference to your answer to (a), how the Rayleigh criterion applies to the diffraction patterns produced by the light emerging from the two slits.
Two lamps emit light of wavelength 620 nm. The lights are observed through a circular aperture of diameter 1.5 mm from a distance of 850 m. Calculate the minimum distance between the lamps so that they are resolved.
Markscheme
large central peak and at least one subsidiary maximum on each side;
minima have intensity of zero and intensity of secondary maxima at most 25 % of central maximum; } (judge by eye)
explanation of resolving – seeing images as being from separate objects;
idea of diffraction patterns overlapping;
central maximum being at least as far from companion as the first minimum;
Marking points may be seen on graph in (a).
Marking points may be seen from diffraction pattern showing resultant intensity from two sources with a slight dip in the centre.
equating \(1.22\frac{\lambda }{b}\) to \(\frac{x}{D}\);
0.43 (m);
Examiners report
The majority could correctly sketch the diffraction pattern and only a few showed non-zero intensity at the minima. The definition of Rayleigh’s criterion was well known but candidates found it difficult to gain full marks explaining how the Rayleigh criterion applies to diffraction patterns, as asked. The calculation was well-attempted.
The majority could correctly sketch the diffraction pattern and only a few showed non-zero intensity at the minima. The definition of Rayleigh’s criterion was well known but candidates found it difficult to gain full marks explaining how the Rayleigh criterion applies to diffraction patterns, as asked. The calculation was well-attempted.
The majority could correctly sketch the diffraction pattern and only a few showed non-zero intensity at the minima. The definition of Rayleigh’s criterion was well known but candidates found it difficult to gain full marks explaining how the Rayleigh criterion applies to diffraction patterns, as asked. The calculation was well-attempted.
This question is about two-source interference.
Coherent light is incident at right angles to a double slit. An interference pattern is observed on a distant screen.
The number of slits is now increased. State and explain the effect, if any, this has on the appearance of the bright fringes.
Markscheme
brighter / more intense
sharper / more well-defined
Examiners report
This question is about a double-slit experiment.
Coherent monochromatic light is incident on two narrow rectangular slits. The diagram shows the fringes produced on a screen that is some distance from the slits. M is the middle of the central bright fringe and P is the middle of the third bright fringe.
Explain why an interference pattern is produced on the screen.
The two slits are separated by 2.2 mm and the distance from the slits to the screen is 1.8 m. The wavelength of the light is 650 nm. Calculate the distance MP.
Markscheme
reference to:
diffraction at slits / slits are coherent sources;
path/phase difference;
constructive and destructive interference;
Do not reward just “interference” as this is mentioned in the question.
for single fringe: \(s = \frac{{650 \times {{10}^{ - 9}} \times 1.8}}{{2.2 \times {{10}^{ - 3}}}}\left( { = 5.3 \times {{10}^{ - 4}}\left( {\rm{m}} \right)} \right)\); } (also award this mark if the factor of 3 is seen in the numerator)
distance \(MP = \left( {5.3 \times {{10}^{ - 4}} \times 3 = } \right)1.6 \times {10^{ - 3}}\left( {\rm{m}} \right)\);
Allow ECF from first marking point.
Award [2] for a bald correct answer.
Examiners report
In part (a) diffraction at each slit, followed by a path difference and subsequent constructive or destructive interference was very often given, but sometimes in a clumsy fashion. It is evident that not all candidates take 30s to plan the order in which they are going to present the steps in their argument.
Part (b) was not difficult, but many lost 1 mark for not using n = 3. Highlight this fact in the stem and these kind of careless errors can be avoided.
This question is about standing waves and the Doppler effect.
The horn of a train can be modeled as a pipe with one open end and one closed end. The speed of sound in air is 330ms–1.
On leaving the station, the train blows its horn. Both the first harmonic and the next highest harmonic are produced by the horn. The difference in frequency between the harmonics emitted by the horn is measured as 820 Hz.
(i) Deduce that the length of the horn is about 0.20 m.
(ii) Show that the frequency of the first harmonic is about 410 Hz.
(i) Describe what is meant by the Doppler effect.
(ii) The train approaches a stationary observer at a constant velocity of 50ms–1 and sounds its horn at the same frequency as in (a)(ii). Calculate the frequency of the sound as measured by the observer.
Markscheme
(i) \({f_1} = \frac{v}{{4L}}\), \({f_2} = 3{f_1} = \frac{{3v}}{{4L}}\);
\({f_2} - {f_1} = \frac{v}{{2L}} = 820\left( {{\rm{Hz}}} \right)\);
\(L = \frac{{330}}{{2 \times 820}}\);
(L=0.20m)
(ii) \(\lambda = 4L = 0.80\left( {\rm{m}} \right)\);
\(f = \left( {\frac{{330}}{{0.8}}} \right) = 413 {\rm{Hz}}\);
This is a question testing units for this option. Do not award second marking point for an incorrect or missing unit.
(i) a change in the observed frequency/wavelength of a wave;
when there is relative motion of observer and source;
(ii) \(f'\left( { = f\frac{v}{{v - {u_s}}}} \right) = 410 \times \frac{{330}}{{330 - 50}}\);
\(f' = 480\left( {{\rm{Hz}}} \right)\);
Allow ECF from (a)(ii).
Examiners report
This question is about the Doppler effect in sound.
A fire engine is travelling at a constant velocity towards a stationary observer. Its siren emits a note of constant frequency. As the engine passes close to the observer, the frequency of the note perceived by the observer decreases. Explain this decrease in terms of the wavefronts of the note emitted by the siren.
The frequency of the note emitted by the siren is 400 Hz. After the fire engine has passed, the frequency of the note detected by the observer is 360 Hz. Calculate the speed of the fire engine. (Take the speed of sound in air to be 340 ms–1.)
Markscheme
diagram showing (non concentric) wavefronts closer together in front/further apart behind source;
frequency is higher as source approaches (because more wavefronts are received per unit of time);
frequency is lower as source recedes (because fewer waverfronts are received per unit of time);
\(360 = 400\left( {\frac{{340}}{{340 + {u_{\rm{s}}}}}} \right)\);
us=38ms–1;
Award [2] for a bald correct answer.
Examiners report
This question is about resolution.
Light from two monochromatic point sources passes through a circular aperture and is observed on a screen.
The graph shows how the intensity I of the light on the screen varies with the angle θ .
The two sources are just resolved according to the Rayleigh criterion.
State what is meant by resolved in this context.
The wavelength of the light from the two sources is 528 nm. The distance of the two sources from the aperture is 1.60 m.
Using data from the graph opposite, determine the
(i) separation of the two sources.
(ii) diameter of the aperture.
Markscheme
the two sources are seen as two distinct sources / two distinct images are formed / the central maximum of one source coincides with the first minimum of the other;
(i) realization that the diffraction angle of the one source diffraction pattern is at 0.008 radians;
and so separation (=1.60×0.008=1.28)≈0.013m;
(ii) \(\left( {1.22\frac{{528 \times {{10}^{ - 9}}}}{b} = 0.008 \Rightarrow } \right)b = 0.081{\rm{mm}}\);
Examiners report
This question is about the Ω– particle.
The Ω– particle is a baryon which contains only strange quarks.
This question is about laser light.
Deduce the strangeness of the Ω– particle.
The Feynman diagram shows a quark change that gives rise to a possible decay of the Ω– particle.
(i) Identify X.
(ii) Identify Y.
The number of lines per millimetre in the diffraction grating in (b) is reduced. Describe the effects of this change on the fringe pattern in (b).
Markscheme
-3;
(i) anti u (quark) /\(\bar u\);
(ii) W–;
principal maxima broaden;
secondary maxima appear;
Examiners report
Many candidates knew about the idea of strangeness, but did not assign a numerical value.
Was reasonably well answered.
There were almost no correct answers. Candidates clearly need a lot of practice answering questions on the diffraction grating.
This question is about resolution.
A car is travelling along a straight road at night. To a distant observer the two headlamps of the car appear as a single point source. With the aid of an appropriately labelled sketch graph, explain this observation.
Markscheme
graph: [2 max]
correct single slit diffraction pattern with appropriate labelling (eg angle/θ) of horizontal axis;
identical diffraction pattern with peak separated by less than half the width of central maximum;
explanation: [2 max]
light from each lamp produces a diffraction pattern on retina of eye;
some statement/Rayleigh criterion quoted to the effect that because the minimum of one falls too close to the maximum of the other they cannot be resolved, so diffraction pattern looks the same as that from a single lamp/source;
Examiners report
This question is about two-source interference.
Light from a monochromatic source is incident at right angles to two slits. After passing through the slits the light is incident on a distant screen. Point M is the mid-point of the screen.
The separation of the slits is large compared to their width. A pattern of light and dark fringes is observed on the screen.
(i) State the phenomenon that enables light to reach point M on the screen.
(ii) On the axes below, sketch the intensity of light as observed on the screen as a function of the angle θ . (You do not have to put any numbers on the axes.)
(iii) The distance of the screen from the slits is 1.8 m and the slit separation is 0.12 mm. The wavelength of the light is 650 nm. Point Q on the screen shows the position of the first dark fringe.
Calculate the distance MQ.
Suggest why, even though there are dark fringes in the pattern, no energy is lost.
Markscheme
(i) diffraction;
(ii) correct general shape (cos2θ) touching the horizontal axis;
constant amplitude;
equally spaced maxima;
Diagram must have at least three fringes.
Award [0] for single slit diffraction pattern.
Award [3] for correct graph that shows modulation by single slit diffraction.
(iii) \({\rm{MQ}} = \frac{1}{2}\frac{{\lambda D}}{d}\);
\({\rm{MQ}} = \left( {\frac{{650 \times {{10}^{ - 9}} \times 1.80}}{{2 \times 0.12 \times {{10}^{ - 3}}}} = } \right)4.9{\rm{mm}}\);
the energy gets redistributed/the total energy in the pattern is the same as the total emitted energy;
the energy that would have appeared at minima now appears at the maxima;
Examiners report
This question is about interference of light at two parallel slits.
State the condition necessary to observe interference between two light sources.
The diagram below shows an arrangement for observing a double slit interference pattern. A parallel beam of coherent light of wavelength 410 nm is incident on two parallel narrow slits separated by 0.30 mm. A screen is placed 1.60 m beyond the slits.
Calculate the fringe spacing on the screen.
The slits in (b) are replaced by a large number of slits of the same width and separation as the double slit. Describe the effects that this change will have on the appearance of the fringes on the screen.
Markscheme
the light from the sources must be coherent / phase difference must be constant (allow “in phase”) / the electric fields must have the same polarization;
fringe spacing=\(\frac{{1.60{\rm{m}} \times {\rm{410nm}}}}{{0.30{\rm{mm}}}}\);
2.2 mm;
Award [2 max] for a response that makes use of nλ in the double slit formula
Award ECF [1 max] if answer is for a value of n greater than 1.
Award [2] for a bald correct answer.
sharper fringes / OWTTE;
brighter;
same spacing;
Examiners report
This question is about diffraction and polarization.
Light from a monochromatic point source S1 is incident on a narrow, rectangular slit.
After passing through the slit the light is incident on a screen. The distance between the slit and screen is very large compared with the width of the slit.
(i) On the axes below, sketch the variation with angle of diffraction θ of the relative intensity I of the light diffracted at the slit.
(ii) The wavelength of the light is 480 nm. The slit width is 0.1 mm and its distance from the screen is 1.2 m. Determine the width of the central diffraction maximum observed on the screen.
Judy looks at two point sources identical to the source S1 in (a). The distance between the sources is 8.0 mm and Judy’s eye is at a distance d from the sources.
Estimate the value of d for which the images of the two sources formed on the retina of Judy’s eye are just resolved.
The light from a point source is unpolarized. The light can be polarized by passing it through a polarizer.
Explain, with reference to the electric (field) vector of unpolarized light and polarized light, the term polarizer.
Markscheme
(i)
overall correct shape with central maxima at θ=0; { (only one secondary maximum required each side of θ=0)
secondary maximum no greater than ¼ intensity of central maximum; { (judge by eye)
(ii) \(\theta = \frac{\lambda }{b} = \frac{x}{D}\) (where x is the half width of central maximum);
\(2x = 2\frac{{D\lambda }}{b}\);
\(\left( {\frac{{2 \times 1.2 \times 4.8 \times {{10}^{ - 7}}}}{{{{10}^{ - 4}}}}} \right) = 12{\rm{mm}}\);
diameter of pupil =3.0 mm; (accept answers in the range of 2.0 mm to 5.0 mm)
\(\theta = \left( {1.22 \times \frac{\lambda }{b} = 1.22 \times \frac{{4.8 \times {{10}^{ - 7}}}}{{3.0 \times {{10}^{ - 3}}}} = } \right)1.95 \times {10^{ - 4}}\left( {{\rm{rad}}} \right)\);
\(d = \frac{{8.0 \times {{10}^{ - 3}}}}{{1.95 \times {{10}^{ - 4}}}} = 41{\rm{m}}\); (accept answer in the range of 20m to 70m)
in unpolarized light the plane of vibration of the electric (field) vector is continually changing / OWTTE;
in polarized light the electric vector vibrates in one plane only;
a polarizer is made of material that absorbs/transmits either the horizontal or vertical component/only one component of the electric vector;
Examiners report
This question is about resolution.
Two point sources S1 and S2 emit monochromatic light of the same wavelength. The light is incident on a small aperture A and is then brought to focus on a screen.
The images of the two sources on the screen are just resolved according to the Rayleigh criterion. Sketch, using the axes below, how the relative intensity I of light on the screen varies with distance along the screen d.
A car is travelling at night along a straight road. Diane is walking towards the car. She sees the headlights of the car as one single light. Estimate, using the data below, the separation d between Diane and the car at which, according to the Rayleigh criterion, Diane will just be able to see the headlights as two separate sources.
Distance between the headlights = 1.4 m
Average wavelength of light emitted by the headlights = 500 nm
Diameter of the pupils of Diane’s eyes = 1.9 mm
The light from the car headlights in (b) is not polarized. State what is meant by polarized light.
Markscheme
correct shape of two diffraction patterns showing central maximum and at least one secondary maximum each side of central maximum;
intensity of secondary maxima no greater than one third intensity of central maxima; } (judge by eye)
first minimum of one pattern coincident with central maximum of other pattern;
or
Allow just the approximate dotted resultant intensity patterns:
correct pattern of two symmetrical principal maxima;
with local minimum between them;
at least one secondary maximum on each side which are no more than \(\frac{1}{3}\) of the intensity of the principal maxima;
angular separation for resolution=\(1.22\frac{\lambda }{b} = 1.22 \times \frac{{5.0 \times {{10}^{ - 7}}}}{{1.9 \times {{10}^{ - 3}}}} = \left( {3.21 \times {{10}^{ - 4}}} \right)\left( {{\rm{rad}}} \right)\);
=\(\frac{{1.4}}{d}\);
d=4.4(km);
Award [2 max] if 1.22 not used and answer is 5.3 km.
Award [3] for a bald correct answer.
light in which the electric/magnetic field (vector) vibrates only in one plane/direction;
Examiners report
This question is about diffraction and resolution.
Monochromatic light is incident on a narrow rectangular slit.
The light is observed on a screen far from the slit. The graph shows the variation with angle θ of the relative intensity for light of wavelength 7.0×10–7m.
Estimate the width of the slit.
On the graph, sketch the variation of the relative intensity with θ when the wavelength of the light is reduced.
State and explain, with reference to your sketch in (b), whether it is easier to resolve two objects in blue light or in red light.
Markscheme
diffraction angle=0.05 rad;
\(b = \left( {\frac{\lambda }{\theta } = \frac{{7.0 \times {{10}^{ - 7}}}}{{0.050}} = } \right)1.4 \times {10^{ - 5}}\left( {\rm{m}} \right)\); (do not accept use of 1.22)
Award [2] for a bald correct answer.
same shape with narrower central maximum;
Ignore height of intensity peak.
blue light gives better resolution;
blue light has shorter wavelength than red light;
giving smaller angle of diffraction;
Allow reverse argument for red light.
Examiners report
Parts (a) and (b) on single slit diffraction were well answered.
Parts (a) and (b) on single slit diffraction were well answered.
However there were fewer correct answers for part (c) where effect of the different wavelengths of red and blue light were sometimes confused and the smaller θ interpreted as poorer resolution. Often the ability to resolve was explained incorrectly in terms of the intensity of the graphs drawn.
This question is about laser light.
Laser light is monochromatic and coherent. Explain what is meant by
(i) monochromatic.
(ii) coherent.
A beam of laser light is incident normally on a diffraction grating which has 600 lines per millimetre. A fringe pattern is formed on a screen 2.0 m from the diffraction grating.
The fringe pattern formed on the screen is shown below.
Determine the wavelength of the laser light.
Markscheme
(i) single frequency/wavelength / narrow range of frequencies/wavelengths;
(ii) in phase;
constant phase difference/relationship;
Award [2] for any correct reference to constant phase difference.
\(\theta = {\tan ^{ - 1}}\left[ {\frac{{0.65}}{{2.0}}} \right]\left( { = 18^\circ } \right)\);
recognition that n=1;
\(d = \frac{1}{{600}}\left( { = 0.0017{\rm{mm}}} \right)\);
λ=(=d sin θ = 0.0017 x sin18º) = 520(mm);
Examiners report
(i) was very well done.
Many candidates got one mark for “in phase” in (ii), but few got two marks for “constant phase difference” even though this is the standard definition for coherence. This is a standard question that has been in several papers over the last few years. Teachers and candidates should take note of the following clarification - there can be two sources which are in phase (that is, have exactly the same phase) and so are coherent. There can also be two sources which have different phases at any one instant but have a constant phase difference/relationship and so are coherent. Thus “constant phase difference” is a better answer than “in phase” because “in phase” is a special case of “constant phase difference” (that is, the constant phase difference is zero).
Most candidates used the equation for double-slit interference rather than the equation for diffraction grating. Candidates appear to be far more comfortable with the double-slit case than the diffraction grating case.
This question is about diffraction and resolution.
Two identical sources of electromagnetic radiation, S1 and S2, emit monochromatic coherent waves of wavelength 59 μm. The waves pass through a circular aperture and are incident on a screen.
S1 and S2 are at the same distance from the aperture. The diameter of the aperture is 0.18 mm. The angle between the lines joining the sources to the aperture is 0.25 rad.
S1 is turned on and S2 is turned off.
(i) Show that the angle at which the first minimum of the diffraction pattern occurs is 0.40 rad.
(ii) On the axes below, sketch a graph to show how the intensity I of the radiation from S1 varies with the diffraction angle θ.
Markscheme
(i) \(\theta = \frac{{1.22 \times 59 \times {{10}^{ - 6}}}}{{0.18 \times {{10}^{ - 3}}}}\);
(=0.40rad)
(ii) central symmetrical maximum;
at least one secondary maximum on each side, no more than one third the height of the central maximum; (judge by eye)
minima drawn to zero, ie touching axis at θ=±0.40 (and ±0.80);
Examiners report
This question is about the Doppler effect.
The diagram shows wavefronts in air produced by a stationary source S of sound. The distance between successive wavefronts is equal to the wavelength of the sound. The speed of sound is c.
On the diagram, sketch three successive wavefronts produced when S is moving to the left at a speed of 0.5c.
A source of X-rays rotates on a turntable. Radiation of wavelength 7.5 nm is emitted by the source and undergoes a maximum shift of 0.50 fm. The distance between the source and the detector is large in comparison to the diameter of the turntable.
(i) Determine the speed of a point on the edge of the turntable.
(ii) State the assumption you made in your answer to (b)(i).
Markscheme
3 circular wavefronts;
2 centres/sources of wavefronts move left (by one box);
Drawn circular wavefronts may be larger as in diagram here, or could be equal sized. Both are acceptable.
(i) \(v = \frac{{5 \times {{10}^{ - 16}} \times 3 \times {{10}^8}}}{{7.5 \times {{10}^{ - 9}}}}\);
20(ms-1);
Use of sound equation not acceptable.
(ii) assume speed of X-rays \( = \) c / assume speed of turntable << c;