 Close to the surface of a large mass (like Earth), the effects of gravitation are uniform. Further out, we realise the the gravitational field of a spherical mass is in fact radial. This has implications for how we calculate forces, field strength, potential and energies.
Close to the surface of a large mass (like Earth), the effects of gravitation are uniform. Further out, we realise the the gravitational field of a spherical mass is in fact radial. This has implications for how we calculate forces, field strength, potential and energies.
Key Concepts
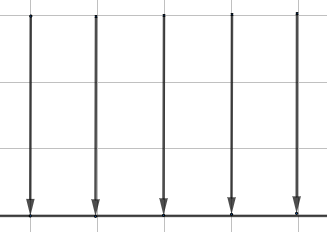
Close to the surface of a large spherical mass, the surface appears horizontal and the gravitational field is uniform. Gravitational field strength is constant (9.81 Nkg-1 on Earth) and field lines are equidistant and parallel.

The direction of field lines is towards the mass producing the field (gravitational forces are always attractive). Because field strength is constant, the force acting on a given mass is constant. We call this weight:
\(F_g=W=mg\)
- \(F_g\) is gravitational force (N)
- \(W\) is weight (N)
- \(m\) is mass (kg)
- \(g\) is gravitational field strength (9.81 Nkg-1 on Earth)
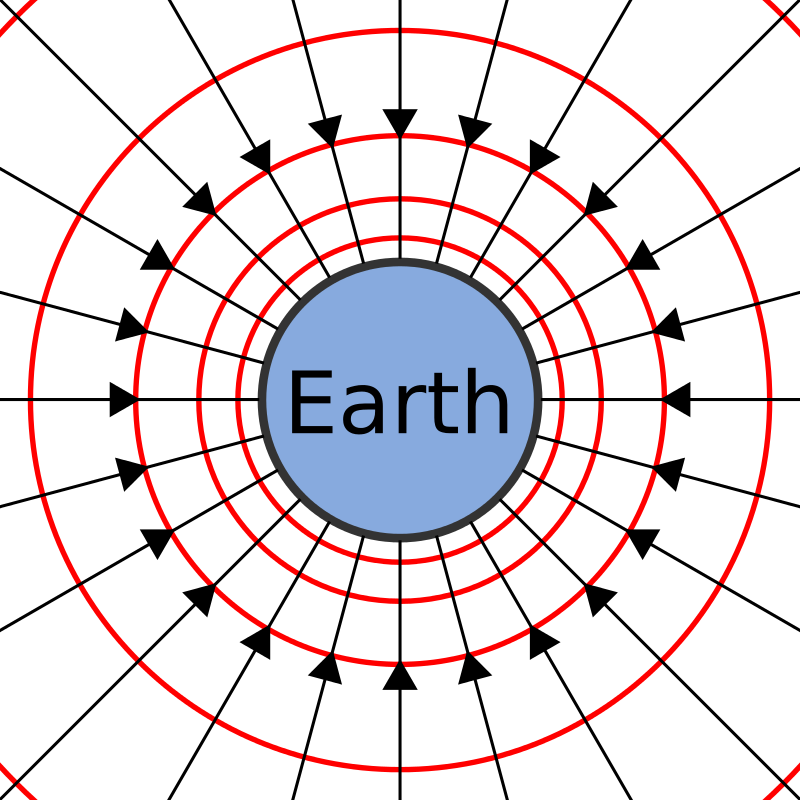
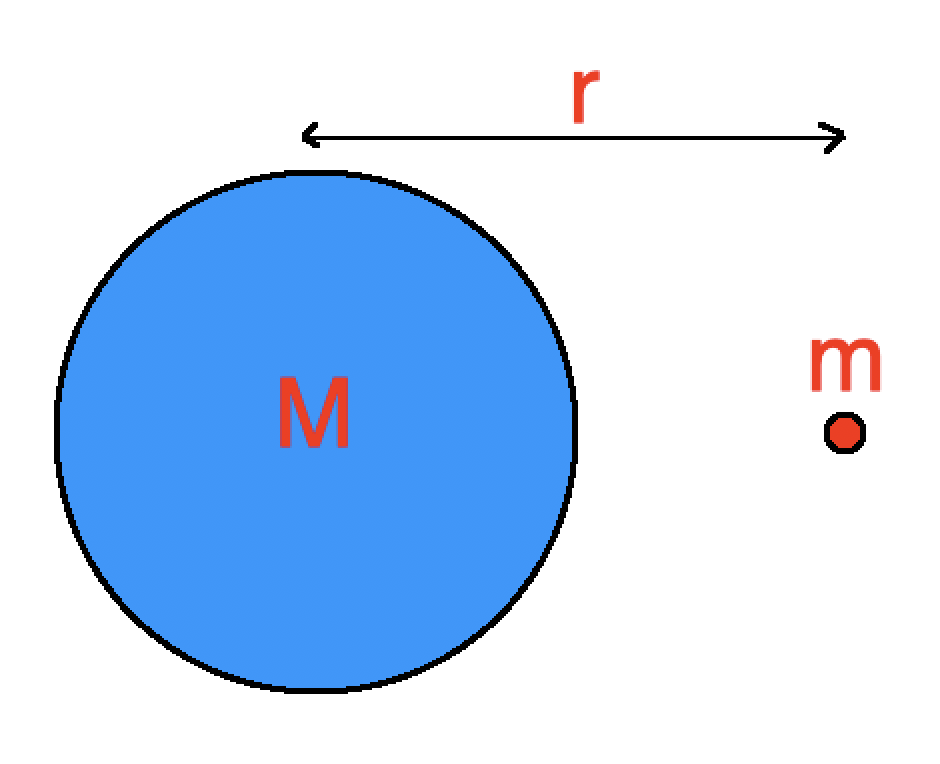
Beyond the distance from a mass at which fields can be assumed to be uniform, gravitational fields from point or spherical masses are radial.
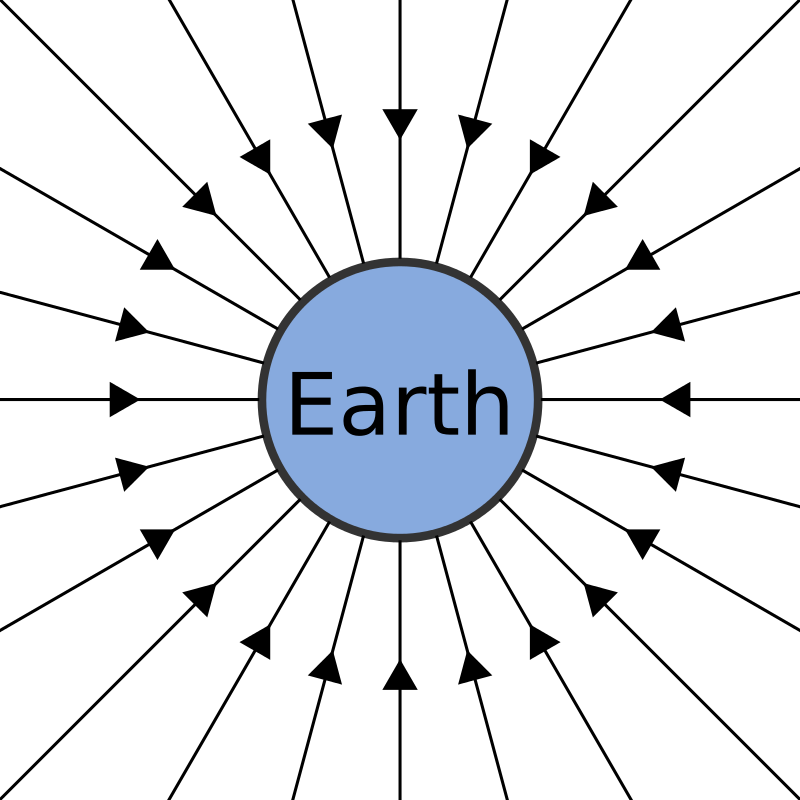
Gravitational force can be calculated from Newton's law:
\(F_g=G{Mm\over r^2}\)
Gravitational field strength is the force per unit mass for a test mass placed in the field:
\(g={F_g\over m}=G{M\over r^2}\)
- \(g\) is gravitational field strength (Nkg-1)
- \(F_g\) is gravitational force (N)
- \(m\) is the mass placed in the field (kg)
- \(G\) is the universal gravitational constant (6.67 × 10-11 m3kg-1s-2)
- \(M\) is the mass producing the field (kg)
- \(r\) is the distance between the centers of masses (m)
Both force and field strength are vector quantities that obey inverse-square law behaviour.
Gravity in space
How much of AHL Gravitational fields have you understood?


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn