IB Questionbank

User interface language: English | Español

Date	May 2018	Marks available	4	Reference code	18M.3.AHL.TZ0.Hca_3
Level	Additional Higher Level	Paper	Paper 3	Time zone	Time zone 0
Command term	Show and Show that	Question number	Hca_3	Adapted from	N/A

Question

Find the value of $\int\limits_4^\infty {\frac{1}{{{x^3}}}{\text{d}}x}$ .

[3]

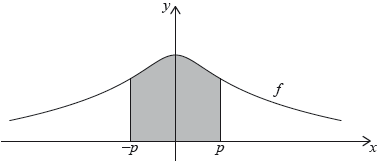
Illustrate graphically the inequality $\sum\limits_{n = 5}^\infty {\frac{1}{{{n^3}}}} < \int\limits_4^\infty {\frac{1}{{{x^3}}}{\text{d}}x} < \sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .

[4]

Hence write down a lower bound for $\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .

[1]

Find an upper bound for $\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\int\limits_4^\infty {\frac{1}{{{x^3}}}{\text{d}}x} = \mathop {{\text{lim}}}\limits_{R \to \infty } \int\limits_4^R {\frac{1}{{{x^3}}}{\text{d}}x}$ (A1)

Note: The above A1 for using a limit can be awarded at any stage.
Condone the use of $\mathop {{\text{lim}}}\limits_{x \to \infty }$ .

Do not award this mark to candidates who use $\infty$ as the upper limit throughout.

= $\mathop {{\text{lim}}}\limits_{R \to \infty } \left[ { - \frac{1}{2}{x^{ - 2}}} \right]_4^R\left( { = \left[ { - \frac{1}{2}{x^{ - 2}}} \right]_4^\infty } \right)$ M1

$= \mathop {{\text{lim}}}\limits_{R \to \infty } \left( { - \frac{1}{2}\left( {{R^{ - 2}} - {4^{ - 2}}} \right)} \right)$

$= \frac{1}{{32}}$ A1

[3 marks]

A1A1A1A1

A1 for the curve
A1 for rectangles starting at $x = 4$
A1 for at least three upper rectangles
A1 for at least three lower rectangles

Note: Award A0A1 for two upper rectangles and two lower rectangles.

sum of areas of the lower rectangles < the area under the curve < the sum of the areas of the upper rectangles so

$\sum\limits_{n = 5}^\infty {\frac{1}{{{n^3}}}} < \int\limits_4^\infty {\frac{1}{{{x^3}}}{\text{d}}x} < \sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ AG

[4 marks]

a lower bound is $\frac{1}{{32}}$ A1

Note: Allow FT from part (a).

[1 mark]

METHOD 1

$\sum\limits_{n = 5}^\infty {\frac{1}{{{n^3}}}} < \frac{1}{{32}}$ (M1)

$\frac{1}{{64}} + \sum\limits_{n = 5}^\infty {\frac{1}{{{n^3}}}} = \frac{1}{{32}} + \frac{1}{{64}}$ (M1)

$\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}} < \frac{3}{{64}}$ , an upper bound A1

Note: Allow FT from part (a).

METHOD 2

changing the lower limit in the inequality in part (b) gives

$\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}} < \int\limits_3^\infty {\frac{1}{{{x^3}}}{\text{d}}x} \left( { < \sum\limits_{n = 3}^\infty {\frac{1}{{{n^3}}}} } \right)$ (A1)

$\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}} < \mathop {{\text{lim}}}\limits_{R \to \infty } \left[ { - \frac{1}{2}{x^{ - 2}}} \right]_3^R$ (M1)

$\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}} < \frac{1}{{18}}$ , an upper bound A1

Note: Condone candidates who do not use a limit.

[3 marks]

Examiners report

[N/A]

Syllabus sections

Topic 5—Calculus » SL 5.5—Integration introduction, areas between curve and x axis

Show 85 related questions

22M.2.AHL.TZ1.6d.ii:
Find the area of the shaded region on the diagram.
18M.2.SL.TZ2.T_1a.i:
Write down the value of a.
17N.2.SL.TZ0.T_4c:
Copy and complete the tree diagram.
19M.2.SL.TZ2.T_1a:
Write down the null hypothesis, H₀, for this test.
22M.1.SL.TZ2.6b.ii:
Calculate the area of this region.
18M.2.SL.TZ1.S_4a:
Write down the coordinates of the vertex of the graph of g.
SPM.1.SL.TZ0.10c:
The three points A(0, 0) , B(3, 10) and C( $a$ , 0) define the vertices of a triangle.

Find the value of $a$ , the $x$ -coordinate of C, such that the area of the triangle is equal to the area of region R.
18M.1.SL.TZ1.S_5a:
Find $\int {{{\left( {f\left( x \right)} \right)}^2}{\text{d}}x}$ .
17N.2.SL.TZ0.T_4f:
Find the probability that the tested adult is allergic to nuts given that the liquid turned blue.
18M.2.SL.TZ2.T_1a.ii:
Write down the value of b.
21M.1.SL.TZ1.13b:
Sieun observes that when the angle is $40 °$ , the ball will travel a horizontal distance of $205.5 m$ .

Find an expression for the function $l (θ)$ .
EXN.2.SL.TZ0.3b.ii:
Hence write down the domain of $h$ .
22M.1.SL.TZ2.6b.i:
Write down an integral for the area of the shaded region in diagram 2.
22M.1.SL.TZ2.6c:
Hence, determine the area enclosed between $y = 6 - x$ and $y = 1.5 x^{2} - 2.5 x + 3$ .
22M.1.SL.TZ2.6a:
Calculate the area of the shaded region in diagram 1.
SPM.1.SL.TZ0.10a:
Write down an integral for the area of region R.
22M.1.SL.TZ1.12b:
One year after the company was founded, the profit was $4$ thousand dollars.

Find an expression for $P (t)$ , when $t \geq 0$ .
22M.1.SL.TZ1.6b:
Find the exact area of the shaded region in the painting.
22M.1.SL.TZ1.6c:
Find the area of the unshaded region in the painting.
22M.2.AHL.TZ1.2d:
The goat is tied in the field for $8$ hours.

Find the total volume of grass eaten by the goat during this time.
22M.2.AHL.TZ1.6d.i:
Find the area enclosed by $y = f (x)$ , the $x$ -axis and the line $x = 0.5$ .
21N.1.SL.TZ0.13a.iii:
Hence find the equation of the quadratic curve.
21N.1.SL.TZ0.13a.ii:
Hence form two equations in terms of $a$ and $b$ .
16N.2.SL.TZ0.T_6b:
Express this volume in ${\text{c}}{{\text{m}}^3}$ .
17M.2.SL.TZ2.S_8b.i:
Write down the coordinates of A.
19M.2.SL.TZ2.T_1b:
State the number of degrees of freedom.
19M.2.SL.TZ2.T_1c.i:
the expected frequency of female students who chose to take the Chinese class.
19M.2.SL.TZ2.T_1d:
State whether or not H₀ should be rejected. Justify your statement.
18M.2.SL.TZ1.S_4b:
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
17M.2.SL.TZ2.S_8b.ii:
Write down the rate of change of $f$ at A.
17N.2.SL.TZ0.T_4d:
Find the probability that this adult is allergic to nuts and the liquid turns blue.
SPM.1.SL.TZ0.10b:
Find the area of region R.
19M.1.SL.TZ1.T_12c:
Write down the probability that the second spin is yellow, given that the first spin is blue.
17N.2.SL.TZ0.T_4g:
Estimate the number of employees, from this 38, who are allergic to nuts.
17M.2.SL.TZ2.S_8c.i:
Find the coordinates of B.
18M.3.AHL.TZ0.Hca_3c:
Hence write down a lower bound for $\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .
19M.2.SL.TZ2.T_1e.iii:
Find the probability that at least one of the two students is female.
19M.1.SL.TZ1.T_12a:
Find the probability that both spins are yellow.
16N.2.SL.TZ0.S_6b:
The empty barrel is being filled with water. The volume $V{\text{ }}{{\text{m}}^3}$ of water in the barrel after $t$ minutes is given by $V = 0.8(1 - {{\text{e}}^{ - 0.1t}})$ . How long will it take for the barrel to be half-full?
18M.2.SL.TZ2.S_3b:
The region enclosed by the graph of $f$ , the y-axis and the x-axis is rotated 360° about the x-axis.

Find the volume of the solid formed.
19M.2.SL.TZ2.S_2b:
The region enclosed by the graph of $f$ , the $x$ -axis and the $y$ -axis is rotated 360º about the $x$ -axis. Find the volume of the solid formed.
19M.1.SL.TZ1.T_12b:
Find the probability that at least one of the spins is yellow.
19M.2.SL.TZ2.T_1e.i:
Find the probability that the student does not take the Spanish class.
17N.2.SL.TZ0.T_4a:
Find the probability that this person is not allergic to nuts.
18M.2.SL.TZ1.S_4c:
Find the area of the region enclosed by the graphs of f and g.
17N.2.SL.TZ0.S_5a:
Find the value of $p$ .
17N.2.SL.TZ0.T_4b:
Find the probability that both people chosen are not allergic to nuts.
19M.2.SL.TZ2.S_2a:
Find the $x$ -intercept of the graph of $f$ .
18M.2.SL.TZ2.T_1b.i:
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
18N.2.SL.TZ0.S_10c:
When $t$ = 0, the volume of water in the container is 2.3 m³. It is known that the container is never completely full of water during the 4 hour period.

Find the minimum volume of empty space in the container during the 4 hour period.
19M.2.SL.TZ2.T_1e.ii:
Find the probability that neither of the two students take the Spanish class.
18M.3.AHL.TZ0.Hca_3d:
Find an upper bound for $\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .
17M.2.SL.TZ2.S_8d:
Let $R$ be the region enclosed by the graph of $f$ , the $x$ -axis, the line $x = b$ and the line $x = a$ . The region $R$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
17M.2.SL.TZ2.S_8a:
Find the value of $p$ .
EXN.1.AHL.TZ0.10a.ii:
State in context what this value represents.
EXN.2.SL.TZ0.3c:
Find the range of $h$ .
18N.2.SL.TZ0.S_10a:
Find the volume of the container.
EXN.1.AHL.TZ0.10a.i:
Find $\int_{0}^{5} \frac{1000}{2 + t} d t$ .
18M.1.SL.TZ1.S_5b:
Part of the graph of f is shown in the following diagram.

The shaded region R is enclosed by the graph of f, the x-axis, and the lines x = 1 and x = 9 . Find the volume of the solid formed when R is revolved 360° about the x-axis.
17N.2.SL.TZ0.T_4e:
Find the probability that the liquid turns blue.
18M.3.AHL.TZ0.Hca_3a:
Find the value of $\int\limits_4^\infty {\frac{1}{{{x^3}}}{\text{d}}x}$ .
18M.2.SL.TZ2.S_3a:
Find the x-intercept of the graph of $f$ .
18M.1.SL.TZ2.S_2a:
Find $\int {\left( {6{x^2} - 3x} \right){\text{d}}x}$ .
18N.2.SL.TZ0.S_10b.ii:
During the interval $p$ < $t$ < $q$ , he volume of water in the container increases by $k$ m³. Find the value of $k$ .
17N.2.SL.TZ0.S_5b:
The following diagram shows part of the graph of $f$ .

The region enclosed by the graph of $f$ , the $x$ -axis and the lines $x = - p$ and $x = p$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
21M.1.SL.TZ2.13a:
Find an expression for $P$ in terms of $x$ .
18M.1.SL.TZ2.T_7c:
Two girls are selected at random.

Calculate the probability that one girl answered questions in Mandarin and the other answered questions in Hindi.
21M.1.SL.TZ1.13a:
Determine whether the graph of $l$ against $θ$ is increasing or decreasing at $θ = 50 °$ .
21M.2.SL.TZ1.5a.i:
Find $\frac{d y}{d x}$ .
18M.1.SL.TZ2.S_2b:
Find the area of the region enclosed by the graph of $f$ , the x-axis and the lines x = 1 and x = 2 .
16N.2.SL.TZ0.S_6a:
Use the model to find the volume of the barrel.
21M.2.AHL.TZ1.2d.ii:
Hence find the cross-sectional area of the tunnel.
18N.2.SL.TZ0.S_10b.i:
Find the value of $p$ and of $q$ .
21M.1.SL.TZ2.13b:
The company regularly increases the number of cars it produces.

Describe how their profit changes if they increase production to over $30$ cars per month and up to $50$ cars per month. Justify your answer.
17M.2.SL.TZ2.S_8c.ii:
Find the the rate of change of $f$ at B.
21M.2.SL.TZ1.5c.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
21M.2.SL.TZ1.5c.ii:
Hence find the cross-sectional area of the tunnel.
21M.2.AHL.TZ1.2d.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
21N.1.SL.TZ0.13b:
Find the area of the shaded region in Irina’s design.
EXN.2.SL.TZ0.3b.i:
Find the value of $t$ at which the ball hits the ground.
EXN.1.AHL.TZ0.10c:
Determine $\int_{0}^{365} P (t) d t$ and state what it represents.
EXN.1.AHL.TZ0.10b:
Find an expression for $P$ in terms of $t$ .
EXN.2.SL.TZ0.3a:
Find an expression for the height $h$ of the ball at time $t$ .
EXN.2.SL.TZ0.6g:
Use the expression found in (f) to calculate a value for $A$ .
21N.1.SL.TZ0.13a.i:
Write down the value of $c$ .

Hide related questions

Topic 5—Calculus

Question

Markscheme

Examiners report

Syllabus sections

View options