IB Questionbank

User interface language: English | Español

Date	May 2022	Marks available	2	Reference code	22M.1.SL.TZ2.6
Level	Standard Level	Paper	Paper 1	Time zone	Time zone 2
Command term	Write down	Question number	6	Adapted from	N/A

Question

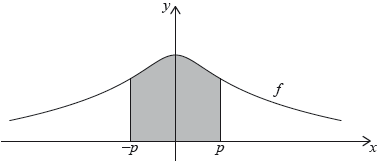
The graphs of $y = 6 - x$ and $y = 1.5 x^{2} - 2.5 x + 3$ intersect at $(2, 4)$ and $(- 1, 7)$ , as shown in the following diagrams.

In diagram 1, the region enclosed by the lines $y = 6 - x$ , $x = - 1$ , $x = 2$ and the $x$ -axis has been shaded.

In diagram 2, the region enclosed by the curve $y = 1.5 x^{2} - 2.5 x + 3$ , and the lines $x = - 1$ , $x = 2$ and the $x$ -axis has been shaded.

Calculate the area of the shaded region in diagram 1.

[2]

Write down an integral for the area of the shaded region in diagram 2.

[2]

b.i.

Calculate the area of this region.

[1]

b.ii.

Hence, determine the area enclosed between $y = 6 - x$ and $y = 1.5 x^{2} - 2.5 x + 3$ .

[2]

Markscheme

EITHER

attempt to substitute $3, 4$ and $7$ into area of a trapezoid formula (M1)

$(A =) \frac{1}{2} (7 + 4) (3)$

given line expressed as an integral (M1)

$(A =) \int_{- 1}^{2} (6 - x) d x$

attempt to sum area of rectangle and area of triangle (M1)

$(A =) 4 \times 3 + \frac{1}{2} (3) (3)$

THEN

$16.5$ (square units) A1

[3 marks]

$(A =) \int_{- 1}^{2} 1.5 x^{2} - 2.5 x + 3 d x$ A1A1

Note: Award A1 for the limits $x = - 1$ , $x = 2$ in correct location. Award A1 for an integral of the quadratic function, $d x$ must be included. Do not accept “ $y$ ” in place of the function, given that two equations are in the question.

[2 marks]

b.i.

$9.75$ (square units) A1

[1 mark]

b.ii.

$16.5 - 9.75$ (M1)

$6.75$ (square units) A1

[2 marks]

Examiners report

There were a variety of methods used or attempted – area of trapezoid, integration, area of triangle plus area of rectangle, area of large rectangle minus area of top triangle, trapezoidal rule. All these methods, except for trapezoidal rule, proved successful for candidates, with the most common being the use of integration.

This was reasonably well done except for a few notation issues such as not including dx with their integrand. Those who attempted integration manually were not successful.

b.i.

[N/A]

b.ii.

Recognition that areas had to be subtracted was very evident.

Syllabus sections

Topic 5—Calculus » SL 5.5—Integration introduction, areas between curve and x axis

Show 85 related questions

22M.2.AHL.TZ1.6d.ii:
Find the area of the shaded region on the diagram.
18M.2.SL.TZ2.T_1a.i:
Write down the value of a.
17N.2.SL.TZ0.T_4c:
Copy and complete the tree diagram.
19M.2.SL.TZ2.T_1a:
Write down the null hypothesis, H₀, for this test.
22M.1.SL.TZ2.6b.ii:
Calculate the area of this region.
18M.2.SL.TZ1.S_4a:
Write down the coordinates of the vertex of the graph of g.
SPM.1.SL.TZ0.10c:
The three points A(0, 0) , B(3, 10) and C( $a$ , 0) define the vertices of a triangle.

Find the value of $a$ , the $x$ -coordinate of C, such that the area of the triangle is equal to the area of region R.
18M.1.SL.TZ1.S_5a:
Find $\int {{{\left( {f\left( x \right)} \right)}^2}{\text{d}}x}$ .
17N.2.SL.TZ0.T_4f:
Find the probability that the tested adult is allergic to nuts given that the liquid turned blue.
18M.2.SL.TZ2.T_1a.ii:
Write down the value of b.
21M.1.SL.TZ1.13b:
Sieun observes that when the angle is $40 °$ , the ball will travel a horizontal distance of $205.5 m$ .

Find an expression for the function $l (θ)$ .
EXN.2.SL.TZ0.3b.ii:
Hence write down the domain of $h$ .
22M.1.SL.TZ2.6c:
Hence, determine the area enclosed between $y = 6 - x$ and $y = 1.5 x^{2} - 2.5 x + 3$ .
22M.1.SL.TZ2.6a:
Calculate the area of the shaded region in diagram 1.
SPM.1.SL.TZ0.10a:
Write down an integral for the area of region R.
22M.1.SL.TZ1.12b:
One year after the company was founded, the profit was $4$ thousand dollars.

Find an expression for $P (t)$ , when $t \geq 0$ .
22M.1.SL.TZ1.6b:
Find the exact area of the shaded region in the painting.
22M.1.SL.TZ1.6c:
Find the area of the unshaded region in the painting.
22M.2.AHL.TZ1.2d:
The goat is tied in the field for $8$ hours.

Find the total volume of grass eaten by the goat during this time.
22M.2.AHL.TZ1.6d.i:
Find the area enclosed by $y = f (x)$ , the $x$ -axis and the line $x = 0.5$ .
21N.1.SL.TZ0.13a.iii:
Hence find the equation of the quadratic curve.
21N.1.SL.TZ0.13a.ii:
Hence form two equations in terms of $a$ and $b$ .
16N.2.SL.TZ0.T_6b:
Express this volume in ${\text{c}}{{\text{m}}^3}$ .
17M.2.SL.TZ2.S_8b.i:
Write down the coordinates of A.
19M.2.SL.TZ2.T_1b:
State the number of degrees of freedom.
19M.2.SL.TZ2.T_1c.i:
the expected frequency of female students who chose to take the Chinese class.
19M.2.SL.TZ2.T_1d:
State whether or not H₀ should be rejected. Justify your statement.
18M.2.SL.TZ1.S_4b:
On the grid above, sketch the graph of g for −2 ≤ x ≤ 4.
17M.2.SL.TZ2.S_8b.ii:
Write down the rate of change of $f$ at A.
17N.2.SL.TZ0.T_4d:
Find the probability that this adult is allergic to nuts and the liquid turns blue.
SPM.1.SL.TZ0.10b:
Find the area of region R.
19M.1.SL.TZ1.T_12c:
Write down the probability that the second spin is yellow, given that the first spin is blue.
17N.2.SL.TZ0.T_4g:
Estimate the number of employees, from this 38, who are allergic to nuts.
17M.2.SL.TZ2.S_8c.i:
Find the coordinates of B.
18M.3.AHL.TZ0.Hca_3c:
Hence write down a lower bound for $\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .
19M.2.SL.TZ2.T_1e.iii:
Find the probability that at least one of the two students is female.
19M.1.SL.TZ1.T_12a:
Find the probability that both spins are yellow.
16N.2.SL.TZ0.S_6b:
The empty barrel is being filled with water. The volume $V{\text{ }}{{\text{m}}^3}$ of water in the barrel after $t$ minutes is given by $V = 0.8(1 - {{\text{e}}^{ - 0.1t}})$ . How long will it take for the barrel to be half-full?
18M.2.SL.TZ2.S_3b:
The region enclosed by the graph of $f$ , the y-axis and the x-axis is rotated 360° about the x-axis.

Find the volume of the solid formed.
19M.2.SL.TZ2.S_2b:
The region enclosed by the graph of $f$ , the $x$ -axis and the $y$ -axis is rotated 360º about the $x$ -axis. Find the volume of the solid formed.
19M.1.SL.TZ1.T_12b:
Find the probability that at least one of the spins is yellow.
19M.2.SL.TZ2.T_1e.i:
Find the probability that the student does not take the Spanish class.
17N.2.SL.TZ0.T_4a:
Find the probability that this person is not allergic to nuts.
18M.2.SL.TZ1.S_4c:
Find the area of the region enclosed by the graphs of f and g.
17N.2.SL.TZ0.S_5a:
Find the value of $p$ .
17N.2.SL.TZ0.T_4b:
Find the probability that both people chosen are not allergic to nuts.
19M.2.SL.TZ2.S_2a:
Find the $x$ -intercept of the graph of $f$ .
18M.2.SL.TZ2.T_1b.i:
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
18N.2.SL.TZ0.S_10c:
When $t$ = 0, the volume of water in the container is 2.3 m³. It is known that the container is never completely full of water during the 4 hour period.

Find the minimum volume of empty space in the container during the 4 hour period.
19M.2.SL.TZ2.T_1e.ii:
Find the probability that neither of the two students take the Spanish class.
18M.3.AHL.TZ0.Hca_3d:
Find an upper bound for $\sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .
17M.2.SL.TZ2.S_8d:
Let $R$ be the region enclosed by the graph of $f$ , the $x$ -axis, the line $x = b$ and the line $x = a$ . The region $R$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
17M.2.SL.TZ2.S_8a:
Find the value of $p$ .
EXN.1.AHL.TZ0.10a.ii:
State in context what this value represents.
EXN.2.SL.TZ0.3c:
Find the range of $h$ .
18N.2.SL.TZ0.S_10a:
Find the volume of the container.
EXN.1.AHL.TZ0.10a.i:
Find $\int_{0}^{5} \frac{1000}{2 + t} d t$ .
18M.1.SL.TZ1.S_5b:
Part of the graph of f is shown in the following diagram.

The shaded region R is enclosed by the graph of f, the x-axis, and the lines x = 1 and x = 9 . Find the volume of the solid formed when R is revolved 360° about the x-axis.
17N.2.SL.TZ0.T_4e:
Find the probability that the liquid turns blue.
18M.3.AHL.TZ0.Hca_3a:
Find the value of $\int\limits_4^\infty {\frac{1}{{{x^3}}}{\text{d}}x}$ .
18M.2.SL.TZ2.S_3a:
Find the x-intercept of the graph of $f$ .
18M.1.SL.TZ2.S_2a:
Find $\int {\left( {6{x^2} - 3x} \right){\text{d}}x}$ .
18N.2.SL.TZ0.S_10b.ii:
During the interval $p$ < $t$ < $q$ , he volume of water in the container increases by $k$ m³. Find the value of $k$ .
17N.2.SL.TZ0.S_5b:
The following diagram shows part of the graph of $f$ .

The region enclosed by the graph of $f$ , the $x$ -axis and the lines $x = - p$ and $x = p$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
21M.1.SL.TZ2.13a:
Find an expression for $P$ in terms of $x$ .
18M.3.AHL.TZ0.Hca_3b:
Illustrate graphically the inequality $\sum\limits_{n = 5}^\infty {\frac{1}{{{n^3}}}} < \int\limits_4^\infty {\frac{1}{{{x^3}}}{\text{d}}x} < \sum\limits_{n = 4}^\infty {\frac{1}{{{n^3}}}}$ .
18M.1.SL.TZ2.T_7c:
Two girls are selected at random.

Calculate the probability that one girl answered questions in Mandarin and the other answered questions in Hindi.
21M.1.SL.TZ1.13a:
Determine whether the graph of $l$ against $θ$ is increasing or decreasing at $θ = 50 °$ .
21M.2.SL.TZ1.5a.i:
Find $\frac{d y}{d x}$ .
18M.1.SL.TZ2.S_2b:
Find the area of the region enclosed by the graph of $f$ , the x-axis and the lines x = 1 and x = 2 .
16N.2.SL.TZ0.S_6a:
Use the model to find the volume of the barrel.
21M.2.AHL.TZ1.2d.ii:
Hence find the cross-sectional area of the tunnel.
18N.2.SL.TZ0.S_10b.i:
Find the value of $p$ and of $q$ .
21M.1.SL.TZ2.13b:
The company regularly increases the number of cars it produces.

Describe how their profit changes if they increase production to over $30$ cars per month and up to $50$ cars per month. Justify your answer.
17M.2.SL.TZ2.S_8c.ii:
Find the the rate of change of $f$ at B.
21M.2.SL.TZ1.5c.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
21M.2.SL.TZ1.5c.ii:
Hence find the cross-sectional area of the tunnel.
21M.2.AHL.TZ1.2d.i:
Write down the integral which can be used to find the cross-sectional area of the tunnel.
21N.1.SL.TZ0.13b:
Find the area of the shaded region in Irina’s design.
EXN.2.SL.TZ0.3b.i:
Find the value of $t$ at which the ball hits the ground.
EXN.1.AHL.TZ0.10c:
Determine $\int_{0}^{365} P (t) d t$ and state what it represents.
EXN.1.AHL.TZ0.10b:
Find an expression for $P$ in terms of $t$ .
EXN.2.SL.TZ0.3a:
Find an expression for the height $h$ of the ball at time $t$ .
EXN.2.SL.TZ0.6g:
Use the expression found in (f) to calculate a value for $A$ .
21N.1.SL.TZ0.13a.i:
Write down the value of $c$ .

Hide related questions

Topic 5—Calculus

Question

Markscheme

Examiners report

Syllabus sections

View options