| Syllabus sections » |
3.2 – Modelling a gas
Description
Nature of science:
Collaboration: Scientists in the 19th century made valuable progress on the modern theories that form the basis of thermodynamics, making important links with other sciences, especially chemistry. The scientific method was in evidence with contrasting but complementary statements of some laws derived by different scientists. Empirical and theoretical thinking both have their place in science and this is evident in the comparison between the unattainable ideal gas and real gases. (4.1)
Understandings:
- Pressure
- Equation of state for an ideal gas
- Kinetic model of an ideal gas
- Mole, molar mass and the Avogadro constant
- Differences between real and ideal gases
Applications and skills:
- Solving problems using the equation of state for an ideal gas and gas laws
- Sketching and interpreting changes of state of an ideal gas on pressure–volume, pressure–temperature and volume–temperature diagrams
- Investigating at least one gas law experimentally
Guidance:
- Students should be aware of the assumptions that underpin the molecular kinetic theory of ideal gases
- Gas laws are limited to constant volume, constant temperature, constant pressure and the ideal gas law
- Students should understand that a real gas approximates to an ideal gas at conditions of low pressure, moderate temperature and low density
Data booklet reference:
Theory of knowledge:
- When does modelling of “ideal” situations become “good enough” to count as knowledge?
Utilization:
- Transport of gases in liquid form or at high pressures/densities is common practice across the globe. Behaviour of real gases under extreme conditions needs to be carefully considered in these situations.
- Consideration of thermodynamic processes is essential to many areas of chemistry (see Chemistry sub-topic 1.3)
- Respiration processes (see Biology sub-topic D.6)
Aims:
- Aim 3: this is a good topic to make comparisons between empirical and theoretical thinking in science
- Aim 6: experiments could include (but are not limited to): verification of gas laws; calculation of the Avogadro constant; virtual investigation of gas law parameters not possible within a school laboratory setting
Directly related questions
- 21M.2.SL.TZ1.3a.ii: State one assumption of the kinetic model of an ideal gas.
- 21M.2.SL.TZ1.3a.ii: State one assumption of the kinetic model of an ideal gas.
- 21M.2.SL.TZ1.a.ii: State one assumption of the kinetic model of an ideal gas.
- 21M.1.SL.TZ1.10: Which aspect of thermal physics is best explained by the molecular kinetic model? A. The...
- 21M.1.SL.TZ1.10: Which aspect of thermal physics is best explained by the molecular kinetic model? A. The...
- 21M.1.SL.TZ1.12: A quantity of 2.00 mol of an ideal gas is maintained at a temperature of 127 ºC in a container of...
- 21M.1.SL.TZ1.12: A quantity of 2.00 mol of an ideal gas is maintained at a temperature of 127 ºC in a container of...
-
21M.1.SL.TZ2.11:
Two identical containers X and Y each contain an ideal gas. X has N molecules of gas at an absolute temperature of T and Y has 3N molecules of gas at an absolute temperature of What is the ratio of the pressures ?
A.
B.
C.
D.
-
21M.1.SL.TZ2.11:
Two identical containers X and Y each contain an ideal gas. X has N molecules of gas at an absolute temperature of T and Y has 3N molecules of gas at an absolute temperature of What is the ratio of the pressures ?
A.
B.
C.
D.
-
18M.2.SL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ1.c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.b.i:
Calculate, in Pa, the new pressure of the gas.
-
21N.1.HL.TZ0.10:
The molar mass of an ideal gas is . A fixed mass of the gas expands at a constant pressure . The graph shows the variation with temperature T of the gas volume V.
What is the gradient of the graph?
A.B.
C.
D.
-
21N.1.HL.TZ0.10:
The molar mass of an ideal gas is . A fixed mass of the gas expands at a constant pressure . The graph shows the variation with temperature T of the gas volume V.
What is the gradient of the graph?
A.B.
C.
D.
-
21N.2.SL.TZ0.2c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.SL.TZ0.2c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.SL.TZ0.c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.SL.TZ0.2b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.SL.TZ0.2b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.SL.TZ0.b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
18M.2.HL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.HL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.HL.TZ2.a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.HL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ2.b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ2.a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.HL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.HL.TZ1.c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
- 18N.2.SL.TZ0.7c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.SL.TZ0.7c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.SL.TZ0.c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.HL.TZ0.9c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.HL.TZ0.9c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.HL.TZ0.c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
-
18N.2.HL.TZ0.9b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
-
18N.2.HL.TZ0.9b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
-
18N.2.HL.TZ0.b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
-
22M.1.SL.TZ1.12:
An ideal gas is maintained at a temperature of 100 K. The variation of the pressure P and of the gas is shown.
What is the quantity of the gas?
A.
B.
C.
D.
-
22M.1.SL.TZ1.12:
An ideal gas is maintained at a temperature of 100 K. The variation of the pressure P and of the gas is shown.
What is the quantity of the gas?
A.
B.
C.
D.
-
22M.2.HL.TZ1.9b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
-
22M.2.HL.TZ1.9b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
-
22M.2.HL.TZ1.b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
- 22M.1.SL.TZ2.12: Which assumption is part of the molecular kinetic model of ideal gases? A. The work done on a...
- 22M.1.SL.TZ2.12: Which assumption is part of the molecular kinetic model of ideal gases? A. The work done on a...
-
22M.1.SL.TZ2.10:
A quantity of an ideal gas is at a temperature T in a cylinder with a movable piston that traps a length L of the gas. The piston is moved so that the length of the trapped gas is reduced to and the pressure of the gas doubles.
What is the temperature of the gas at the end of the change?
A.
B.
C.
D. -
22M.1.SL.TZ2.10:
A quantity of an ideal gas is at a temperature T in a cylinder with a movable piston that traps a length L of the gas. The piston is moved so that the length of the trapped gas is reduced to and the pressure of the gas doubles.
What is the temperature of the gas at the end of the change?
A.
B.
C.
D. - 22M.1.SL.TZ2.11: What is true for an ideal gas? A. nRT = NkBT B. nRT = kBT C. RT = NkBT D. RT = kBT
- 22M.1.SL.TZ2.11: What is true for an ideal gas? A. nRT = NkBT B. nRT = kBT C. RT = NkBT D. RT = kBT
-
22M.2.SL.TZ2.2a:
Calculate the number of gas particles in the cylinder.
-
22M.2.SL.TZ2.2a:
Calculate the number of gas particles in the cylinder.
-
22M.2.SL.TZ2.a:
Calculate the number of gas particles in the cylinder.
- 22M.2.SL.TZ2.2b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.2b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22M.2.SL.TZ2.b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
-
19M.2.HL.TZ2.2ci:
Calculate the ratio .
-
19M.2.HL.TZ2.2ci:
Calculate the ratio .
-
19M.2.HL.TZ2.ci:
Calculate the ratio .
-
19M.2.HL.TZ2.2cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
-
19M.2.HL.TZ2.2cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
-
19M.2.HL.TZ2.cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.2.HL.TZ2.dii: Suggest, in terms of conservation of energy, the cause for the above change.
-
19M.2.HL.TZ2.2b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.HL.TZ2.2b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.HL.TZ2.b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.SL.TZ1.4a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.4a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.4b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.2.SL.TZ1.4b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.2.SL.TZ1.b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.2.SL.TZ2.2b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.2b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.2dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
-
19M.2.SL.TZ2.2dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
-
19M.2.SL.TZ2.dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
-
19M.1.SL.TZ2.11:
The temperature of a fixed mass of an ideal gas changes from 200 °C to 400 °C.
What is ?
A. 0.50
B. 0.70
C. 1.4
D. 2.0
-
19M.1.SL.TZ2.11:
The temperature of a fixed mass of an ideal gas changes from 200 °C to 400 °C.
What is ?
A. 0.50
B. 0.70
C. 1.4
D. 2.0
-
19M.2.SL.TZ2.2di:
Calculate the ratio .
-
19M.2.SL.TZ2.2di:
Calculate the ratio .
-
19M.2.SL.TZ2.di:
Calculate the ratio .
-
19M.2.SL.TZ2.2c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19M.2.SL.TZ2.2c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19M.2.SL.TZ2.c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19N.2.SL.TZ0.2b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.2b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.2b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
-
19N.2.SL.TZ0.2b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
-
19N.2.SL.TZ0.b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
-
19N.2.SL.TZ0.2a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
19N.2.SL.TZ0.2a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
19N.2.SL.TZ0.a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
22N.1.SL.TZ0.10:
Three statements about Boltzmann’s constant kB are:
I. kB has a unit of J K−1
II. kB
III. kB
Which statements are correct?
A. I and II onlyB. I and III only
C. II and III only
D. I, II and III
-
22N.1.SL.TZ0.10:
Three statements about Boltzmann’s constant kB are:
I. kB has a unit of J K−1
II. kB
III. kB
Which statements are correct?
A. I and II onlyB. I and III only
C. II and III only
D. I, II and III
-
22N.1.HL.TZ0.11:
Gases in the atmosphere are compounds of , , and .
Four of these gases are CO2, N2O, CH4 and H2O. A pure sample of each gas is produced. Each sample has the same mass.
Which sample contains the greatest number of molecules?
A. N2OB. H2O
C. CO2
D. CH4
-
22N.1.HL.TZ0.11:
Gases in the atmosphere are compounds of , , and .
Four of these gases are CO2, N2O, CH4 and H2O. A pure sample of each gas is produced. Each sample has the same mass.
Which sample contains the greatest number of molecules?
A. N2OB. H2O
C. CO2
D. CH4
- 22N.2.HL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.HL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.HL.TZ0.b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.HL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.HL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.HL.TZ0.b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 17N.1.SL.TZ0.9: What does the constant n represent in the equation of state for an ideal gas pV = nRT? A. The...
- 17N.1.SL.TZ0.9: What does the constant n represent in the equation of state for an ideal gas pV = nRT? A. The...
- 17N.1.SL.TZ0.11: Under what conditions of pressure and temperature does a real gas approximate to an ideal gas?
- 17N.1.SL.TZ0.11: Under what conditions of pressure and temperature does a real gas approximate to an ideal gas?
-
17N.1.HL.TZ0.12:
Unpolarized light of intensity I0 is incident on a polarizing filter. Light from this filter is incident on a second filter, which has its axis of polarization at 30˚ to that of the first filter.
The value of cos 30˚ is . What is the intensity of the light emerging through the second filter?
A. I0
B. I0
C. I0
D. I0
-
17N.1.HL.TZ0.12:
Unpolarized light of intensity I0 is incident on a polarizing filter. Light from this filter is incident on a second filter, which has its axis of polarization at 30˚ to that of the first filter.
The value of cos 30˚ is . What is the intensity of the light emerging through the second filter?
A. I0
B. I0
C. I0
D. I0
- 18M.1.SL.TZ1.10: A fixed mass of an ideal gas is trapped in a cylinder of constant volume and its temperature is...
- 18M.1.SL.TZ1.10: A fixed mass of an ideal gas is trapped in a cylinder of constant volume and its temperature is...
-
18M.1.SL.TZ1.12:
A sealed cylinder of length l and cross-sectional area A contains N molecules of an ideal gas at kelvin temperature T.
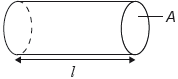
What is the force acting on the area of the cylinder marked A due to the gas?
A.
B.
C.
D.
-
18M.1.SL.TZ1.12:
A sealed cylinder of length l and cross-sectional area A contains N molecules of an ideal gas at kelvin temperature T.

What is the force acting on the area of the cylinder marked A due to the gas?
A.
B.
C.
D.
-
18M.2.SL.TZ1.2a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.2a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.SL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.SL.TZ2.b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ1.2b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.2.HL.TZ1.2b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.2.HL.TZ1.b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.1.HL.TZ2.9:
Q and R are two rigid containers of volume 3V and V respectively containing molecules of the same ideal gas initially at the same temperature. The gas pressures in Q and R are p and 3p respectively. The containers are connected through a valve of negligible volume that is initially closed.

The valve is opened in such a way that the temperature of the gases does not change. What is the change of pressure in Q?
A. +p
B.
C.
D. –p
-
18M.1.HL.TZ2.9:
Q and R are two rigid containers of volume 3V and V respectively containing molecules of the same ideal gas initially at the same temperature. The gas pressures in Q and R are p and 3p respectively. The containers are connected through a valve of negligible volume that is initially closed.

The valve is opened in such a way that the temperature of the gases does not change. What is the change of pressure in Q?
A. +p
B.
C.
D. –p
-
18N.1.SL.TZ0.11:
A container is filled with a mixture of helium and oxygen at the same temperature. The molar mass of helium is 4 g mol–1 and that of oxygen is 32 g mol–1.
What is the ratio ?
A.
B.
C.
D. 8
-
18N.1.SL.TZ0.11:
A container is filled with a mixture of helium and oxygen at the same temperature. The molar mass of helium is 4 g mol–1 and that of oxygen is 32 g mol–1.
What is the ratio ?
A.
B.
C.
D. 8
-
18N.1.SL.TZ0.12:
Container X contains 1.0 mol of an ideal gas. Container Y contains 2.0 mol of the ideal gas. Y has four times the volume of X. The pressure in X is twice that in Y.
What is ?
A.
B.
C. 1
D. 2
-
18N.1.SL.TZ0.12:
Container X contains 1.0 mol of an ideal gas. Container Y contains 2.0 mol of the ideal gas. Y has four times the volume of X. The pressure in X is twice that in Y.
What is ?
A.
B.
C. 1
D. 2
-
18N.2.SL.TZ0.7b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
-
18N.2.SL.TZ0.7b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
-
18N.2.SL.TZ0.b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
-
19M.2.HL.TZ2.2a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.2a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.1.SL.TZ1.13:
A gas storage tank of fixed volume V contains N molecules of an ideal gas at temperature T. The pressure at kelvin temperature T is 20 MPa. molecules are removed and the temperature changed to 2T. What is the new pressure of the gas?
A. 10 MPa
B. 15 MPa
C. 30 MPa
D. 40 MPa
-
19M.1.SL.TZ1.13:
A gas storage tank of fixed volume V contains N molecules of an ideal gas at temperature T. The pressure at kelvin temperature T is 20 MPa. molecules are removed and the temperature changed to 2T. What is the new pressure of the gas?
A. 10 MPa
B. 15 MPa
C. 30 MPa
D. 40 MPa
-
19M.1.HL.TZ2.14:
Cylinder X has a volume and contains 3.0 mol of an ideal gas. Cylinder Y has a volume and contains 2.0 mol of the same gas.
The gases in X and Y are at the same temperature . The containers are joined by a valve which is opened so that the temperatures do not change.
What is the change in pressure in X?
A.
B.
C.
D.
-
19M.1.HL.TZ2.14:
Cylinder X has a volume and contains 3.0 mol of an ideal gas. Cylinder Y has a volume and contains 2.0 mol of the same gas.
The gases in X and Y are at the same temperature . The containers are joined by a valve which is opened so that the temperatures do not change.
What is the change in pressure in X?
A.
B.
C.
D.
-
19M.1.SL.TZ2.12:
A container holds 20 g of argon-40() and 40 g of neon-20 () .
What is in the container?
A. 0.25
B. 0.5
C. 2
D. 4
-
19M.1.SL.TZ2.12:
A container holds 20 g of argon-40() and 40 g of neon-20 () .
What is in the container?
A. 0.25
B. 0.5
C. 2
D. 4
-
19M.2.SL.TZ2.2a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.2a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
- 19N.1.SL.TZ0.10: An ideal gas is in a closed container. Which changes to its volume and temperature when taken...
- 19N.1.SL.TZ0.10: An ideal gas is in a closed container. Which changes to its volume and temperature when taken...
-
19N.1.SL.TZ0.11:
Two flasks P and Q contain an ideal gas and are connected with a tube of negligible volume compared to that of the flasks. The volume of P is twice the volume of Q.
P is held at a temperature of 200 K and Q is held at a temperature of 400 K.
What is mass of ?
A.
B.
C. 4
D. 8
-
19N.1.SL.TZ0.11:
Two flasks P and Q contain an ideal gas and are connected with a tube of negligible volume compared to that of the flasks. The volume of P is twice the volume of Q.
P is held at a temperature of 200 K and Q is held at a temperature of 400 K.
What is mass of ?
A.
B.
C. 4
D. 8
- 19N.1.HL.TZ0.9: Under which conditions of pressure and density will a real gas approximate to an ideal gas?
- 19N.1.HL.TZ0.9: Under which conditions of pressure and density will a real gas approximate to an ideal gas?
- 20N.1.SL.TZ0.11: An ideal gas of constant mass is heated in a container of constant volume. What is the reason...
- 20N.1.SL.TZ0.11: An ideal gas of constant mass is heated in a container of constant volume. What is the reason...
-
20N.1.SL.TZ0.12:
A substance in the gas state has a density about times less than when it is in the liquid state. The diameter of a molecule is . What is the best estimate of the average distance between molecules in the gas state?
A.
B.
C.
D.
-
20N.1.SL.TZ0.12:
A substance in the gas state has a density about times less than when it is in the liquid state. The diameter of a molecule is . What is the best estimate of the average distance between molecules in the gas state?
A.
B.
C.
D.
- 20N.1.HL.TZ0.7: What is not an assumption of the kinetic model of an ideal gas? A. Attractive forces between...
- 20N.1.HL.TZ0.7: What is not an assumption of the kinetic model of an ideal gas? A. Attractive forces between...
-
20N.1.HL.TZ0.9:
Two containers X and Y are maintained at the same temperature. X has volume and Y has volume . They both hold an ideal gas. The pressure in X is and the pressure in Y is . The containers are then joined by a tube of negligible volume. What is the final pressure in the containers?
A.
B.
C.
D.
-
20N.1.HL.TZ0.9:
Two containers X and Y are maintained at the same temperature. X has volume and Y has volume . They both hold an ideal gas. The pressure in X is and the pressure in Y is . The containers are then joined by a tube of negligible volume. What is the final pressure in the containers?
A.
B.
C.
D.
-
21M.2.SL.TZ1.3a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
-
21M.2.SL.TZ1.3a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
-
21M.2.SL.TZ1.a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
-
21M.2.SL.TZ2.2a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.2a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.2b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.2b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.2c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
-
21M.2.SL.TZ2.2c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
-
21M.2.SL.TZ2.c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
- 21M.1.HL.TZ1.10: Two ideal gases X and Y are at the same temperature. The mass of a particle of gas X is larger...
- 21M.1.HL.TZ1.10: Two ideal gases X and Y are at the same temperature. The mass of a particle of gas X is larger...
- 21M.1.SL.TZ1.25: What is the relation between the value of the unified atomic mass unit in grams and the value of...
- 21M.1.SL.TZ1.25: What is the relation between the value of the unified atomic mass unit in grams and the value of...
-
21M.1.SL.TZ2.10:
A sample of oxygen gas with a volume of is at . The gas is heated so that it expands at a constant pressure to a final volume of . What is the final temperature of the gas?
A.
B.
C.
D.
-
21M.1.SL.TZ2.10:
A sample of oxygen gas with a volume of is at . The gas is heated so that it expands at a constant pressure to a final volume of . What is the final temperature of the gas?
A.
B.
C.
D.
-
21N.1.SL.TZ0.12:
A fixed mass of an ideal gas has a volume of , a pressure of p and a temperature of . The gas is compressed to the volume of and its pressure increases to 12p. What is the new temperature of the gas?
A.B.
C.
D.
-
21N.1.SL.TZ0.12:
A fixed mass of an ideal gas has a volume of , a pressure of p and a temperature of . The gas is compressed to the volume of and its pressure increases to 12p. What is the new temperature of the gas?
A.B.
C.
D.
-
21N.2.SL.TZ0.2b.i:
Calculate the pressure of the gas.
-
21N.2.SL.TZ0.2b.i:
Calculate the pressure of the gas.
-
21N.2.SL.TZ0.b.i:
Calculate the pressure of the gas.
-
21N.2.HL.TZ0.6d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
21N.2.HL.TZ0.6d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
21N.2.HL.TZ0.d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
- 22N.2.SL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.SL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.SL.TZ0.b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.SL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.SL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.SL.TZ0.b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
23M.1.HL.TZ1.25:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.29:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.29:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.HL.TZ1.25:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.30:
Light of intensity 500 W m−2 is incident on concrete and on snow. 300 W m−2 is reflected from the
concrete and 400 W m−2 is reflected from the snow.What is ?
A.B.
C.
D. 2
-
23M.1.SL.TZ1.30:
Light of intensity 500 W m−2 is incident on concrete and on snow. 300 W m−2 is reflected from the
concrete and 400 W m−2 is reflected from the snow.What is ?
A.B.
C.
D. 2
- 23M.1.SL.TZ2.12: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.10: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.SL.TZ2.12: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.10: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.9: A fixed mass of an ideal gas expands slowly at constant temperature in a container. Three...
- 23M.1.HL.TZ2.9: A fixed mass of an ideal gas expands slowly at constant temperature in a container. Three...
-
23M.1.SL.TZ2.11:
A vessel contains a mass X of helium gas and a mass 2X of oxygen gas.
Molar mass of helium = 4 g
Molar mass of oxygen = 32 g
What is the ?
A.B.
C. 4
D. 8
-
23M.1.SL.TZ2.11:
A vessel contains a mass X of helium gas and a mass 2X of oxygen gas.
Molar mass of helium = 4 g
Molar mass of oxygen = 32 g
What is the ?
A.B.
C. 4
D. 8
- 23M.2.SL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.HL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.HL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.HL.TZ2.a: State the unit for pV in fundamental SI units.
- 23M.2.SL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.SL.TZ2.a: State the unit for pV in fundamental SI units.
- 23M.1.HL.TZ2.27: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
- 23M.1.HL.TZ2.27: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
- 23M.1.SL.TZ2.30: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
- 23M.1.SL.TZ2.30: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
