| Syllabus sections » |
Topic 3: Thermal physics
Description
Overview of the essential ideas for this topic
3.1: Thermal physics deftly demonstrates the links between the macroscopic measurements essential to many scientific models with the microscopic properties that underlie these models.
3.2: The properties of ideal gases allow scientists to make predictions of the behaviour of real gases.
Directly related questions
- 20N.1.SL.TZ0.11: An ideal gas of constant mass is heated in a container of constant volume. What is the reason...
- 20N.1.SL.TZ0.11: An ideal gas of constant mass is heated in a container of constant volume. What is the reason...
-
20N.1.SL.TZ0.12:
A substance in the gas state has a density about times less than when it is in the liquid state. The diameter of a molecule is . What is the best estimate of the average distance between molecules in the gas state?
A.
B.
C.
D.
-
20N.1.SL.TZ0.12:
A substance in the gas state has a density about times less than when it is in the liquid state. The diameter of a molecule is . What is the best estimate of the average distance between molecules in the gas state?
A.
B.
C.
D.
-
20N.1.SL.TZ0.13:
A bicycle of mass comes to rest from speed using the back brake. The brake has a specific heat capacity of and a mass . Half of the kinetic energy is absorbed by the brake.
What is the change in temperature of the brake?
A.
B.
C.
D.
-
20N.1.SL.TZ0.13:
A bicycle of mass comes to rest from speed using the back brake. The brake has a specific heat capacity of and a mass . Half of the kinetic energy is absorbed by the brake.
What is the change in temperature of the brake?
A.
B.
C.
D.
- 20N.1.HL.TZ0.7: What is not an assumption of the kinetic model of an ideal gas? A. Attractive forces between...
- 20N.1.HL.TZ0.7: What is not an assumption of the kinetic model of an ideal gas? A. Attractive forces between...
- 20N.2.SL.TZ0.3b: The sample begins to freeze during the thermal energy transfer. Explain, in terms of the...
- 20N.2.SL.TZ0.3b: The sample begins to freeze during the thermal energy transfer. Explain, in terms of the...
- 20N.2.SL.TZ0.b: The sample begins to freeze during the thermal energy transfer. Explain, in terms of the...
-
20N.2.SL.TZ0.3a(i):
Calculate the thermal energy transferred from the sample during the first minutes.
-
20N.2.SL.TZ0.3a(i):
Calculate the thermal energy transferred from the sample during the first minutes.
-
20N.2.SL.TZ0.a(i):
Calculate the thermal energy transferred from the sample during the first minutes.
-
20N.2.SL.TZ0.3a(ii):
Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer.
-
20N.2.SL.TZ0.3a(ii):
Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer.
-
20N.2.SL.TZ0.a(ii):
Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer.
-
17N.2.SL.TZ0.4b.i:
Determine the energy required to melt all of the ice from –20 °C to water at a temperature of 0 °C.
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3 -
17N.2.SL.TZ0.4b.i:
Determine the energy required to melt all of the ice from –20 °C to water at a temperature of 0 °C.
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3 -
17N.2.SL.TZ0.b.i:
Determine the energy required to melt all of the ice from –20 °C to water at a temperature of 0 °C.
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3 - 17N.1.SL.TZ0.10: A 1.0 kW heater supplies energy to a liquid of mass 0.50 kg. The temperature of the liquid...
- 17N.1.SL.TZ0.10: A 1.0 kW heater supplies energy to a liquid of mass 0.50 kg. The temperature of the liquid...
- 17N.1.SL.TZ0.11: Under what conditions of pressure and temperature does a real gas approximate to an ideal gas?
- 17N.1.SL.TZ0.11: Under what conditions of pressure and temperature does a real gas approximate to an ideal gas?
-
17N.1.HL.TZ0.12:
Unpolarized light of intensity I0 is incident on a polarizing filter. Light from this filter is incident on a second filter, which has its axis of polarization at 30˚ to that of the first filter.
The value of cos 30˚ is . What is the intensity of the light emerging through the second filter?
A. I0
B. I0
C. I0
D. I0
-
17N.1.HL.TZ0.12:
Unpolarized light of intensity I0 is incident on a polarizing filter. Light from this filter is incident on a second filter, which has its axis of polarization at 30˚ to that of the first filter.
The value of cos 30˚ is . What is the intensity of the light emerging through the second filter?
A. I0
B. I0
C. I0
D. I0
-
17N.3.SL.TZ0.1c.ii:
Using an appropriate error calculation, justify the number of significant figures that should be used for your answer to (c)(i).
-
17N.3.SL.TZ0.1c.ii:
Using an appropriate error calculation, justify the number of significant figures that should be used for your answer to (c)(i).
-
17N.3.SL.TZ0.c.ii:
Using an appropriate error calculation, justify the number of significant figures that should be used for your answer to (c)(i).
- 17N.3.SL.TZ0.1c.i: Calculate the energy required to raise the temperature of the water from 75 °C to 85 °C.
- 17N.3.SL.TZ0.1c.i: Calculate the energy required to raise the temperature of the water from 75 °C to 85 °C.
- 17N.3.SL.TZ0.c.i: Calculate the energy required to raise the temperature of the water from 75 °C to 85 °C.
-
17N.2.SL.TZ0.4b.ii:
Outline the difference between the molecular structure of a solid and a liquid.
-
17N.2.SL.TZ0.4b.ii:
Outline the difference between the molecular structure of a solid and a liquid.
-
17N.2.SL.TZ0.b.ii:
Outline the difference between the molecular structure of a solid and a liquid.
- 17N.3.SL.TZ0.1b.i: Determine the gradient of the line at a temperature of 80 °C.
- 17N.3.SL.TZ0.1b.i: Determine the gradient of the line at a temperature of 80 °C.
- 17N.3.SL.TZ0.b.i: Determine the gradient of the line at a temperature of 80 °C.
-
21M.2.SL.TZ1.3b.i:
Estimate the specific latent heat of vaporization of water. State an appropriate unit for your answer.
-
21M.2.SL.TZ1.3b.i:
Estimate the specific latent heat of vaporization of water. State an appropriate unit for your answer.
-
21M.2.SL.TZ1.b.i:
Estimate the specific latent heat of vaporization of water. State an appropriate unit for your answer.
- 21M.2.SL.TZ1.3b.ii: Explain why the temperature of water remains at 100 °C during this time.
- 21M.2.SL.TZ1.3b.ii: Explain why the temperature of water remains at 100 °C during this time.
- 21M.2.SL.TZ1.b.ii: Explain why the temperature of water remains at 100 °C during this time.
-
21M.2.SL.TZ1.3c:
The heater is removed and a mass of 0.30 kg of pasta at −10 °C is added to the boiling water.
Determine the equilibrium temperature of the pasta and water after the pasta is added. Other heat transfers are negligible.
Specific heat capacity of pasta = 1.8 kJ kg−1 K−1
Specific heat capacity of water = 4.2 kJ kg−1 K−1 -
21M.2.SL.TZ1.3c:
The heater is removed and a mass of 0.30 kg of pasta at −10 °C is added to the boiling water.
Determine the equilibrium temperature of the pasta and water after the pasta is added. Other heat transfers are negligible.
Specific heat capacity of pasta = 1.8 kJ kg−1 K−1
Specific heat capacity of water = 4.2 kJ kg−1 K−1 -
21M.2.SL.TZ1.c:
The heater is removed and a mass of 0.30 kg of pasta at −10 °C is added to the boiling water.
Determine the equilibrium temperature of the pasta and water after the pasta is added. Other heat transfers are negligible.
Specific heat capacity of pasta = 1.8 kJ kg−1 K−1
Specific heat capacity of water = 4.2 kJ kg−1 K−1 -
21M.2.SL.TZ1.3a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
-
21M.2.SL.TZ1.3a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
-
21M.2.SL.TZ1.a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
- 21M.2.SL.TZ1.3a.ii: State one assumption of the kinetic model of an ideal gas.
- 21M.2.SL.TZ1.3a.ii: State one assumption of the kinetic model of an ideal gas.
- 21M.2.SL.TZ1.a.ii: State one assumption of the kinetic model of an ideal gas.
- 21M.1.SL.TZ1.10: Which aspect of thermal physics is best explained by the molecular kinetic model? A. The...
- 21M.1.SL.TZ1.10: Which aspect of thermal physics is best explained by the molecular kinetic model? A. The...
-
21M.1.SL.TZ1.11:
When 40 kJ of energy is transferred to a quantity of a liquid substance, its temperature increases by 20 K. When 600 kJ of energy is transferred to the same quantity of the liquid at its boiling temperature, it vaporizes completely at constant temperature. What is
for this substance?
A. 15 K−1
B. 15 K
C. 300 K−1
D. 300 K
-
21M.1.SL.TZ1.11:
When 40 kJ of energy is transferred to a quantity of a liquid substance, its temperature increases by 20 K. When 600 kJ of energy is transferred to the same quantity of the liquid at its boiling temperature, it vaporizes completely at constant temperature. What is
for this substance?
A. 15 K−1
B. 15 K
C. 300 K−1
D. 300 K
- 21M.1.HL.TZ1.10: Two ideal gases X and Y are at the same temperature. The mass of a particle of gas X is larger...
- 21M.1.HL.TZ1.10: Two ideal gases X and Y are at the same temperature. The mass of a particle of gas X is larger...
- 21M.1.SL.TZ1.25: What is the relation between the value of the unified atomic mass unit in grams and the value of...
- 21M.1.SL.TZ1.25: What is the relation between the value of the unified atomic mass unit in grams and the value of...
- 21M.1.SL.TZ1.12: A quantity of 2.00 mol of an ideal gas is maintained at a temperature of 127 ºC in a container of...
- 21M.1.SL.TZ1.12: A quantity of 2.00 mol of an ideal gas is maintained at a temperature of 127 ºC in a container of...
-
21M.1.SL.TZ2.11:
Two identical containers X and Y each contain an ideal gas. X has N molecules of gas at an absolute temperature of T and Y has 3N molecules of gas at an absolute temperature of What is the ratio of the pressures ?
A.
B.
C.
D.
-
21M.1.SL.TZ2.11:
Two identical containers X and Y each contain an ideal gas. X has N molecules of gas at an absolute temperature of T and Y has 3N molecules of gas at an absolute temperature of What is the ratio of the pressures ?
A.
B.
C.
D.
-
21M.1.SL.TZ2.12:
A piece of metal at a temperature of is dropped into an equal mass of water at a temperature of in a container of negligible mass. The specific heat capacity of water is four times that of the metal. What is the final temperature of the mixture?
A.
B.
C.
D.
-
21M.1.SL.TZ2.12:
A piece of metal at a temperature of is dropped into an equal mass of water at a temperature of in a container of negligible mass. The specific heat capacity of water is four times that of the metal. What is the final temperature of the mixture?
A.
B.
C.
D.
- 18M.1.SL.TZ1.10: A fixed mass of an ideal gas is trapped in a cylinder of constant volume and its temperature is...
- 18M.1.SL.TZ1.10: A fixed mass of an ideal gas is trapped in a cylinder of constant volume and its temperature is...
-
18M.1.SL.TZ1.11:
What are the units of the ratio ?
A. no units
B. k
C. k–1
D. k–2
-
18M.1.SL.TZ1.11:
What are the units of the ratio ?
A. no units
B. k
C. k–1
D. k–2
-
18M.2.SL.TZ1.2b.i:
Calculate, in kg, the mass of the gas.
-
18M.2.SL.TZ1.2b.i:
Calculate, in kg, the mass of the gas.
-
18M.2.SL.TZ1.b.i:
Calculate, in kg, the mass of the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.2a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.2a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ1.c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.1.SL.TZ1.12:
A sealed cylinder of length l and cross-sectional area A contains N molecules of an ideal gas at kelvin temperature T.
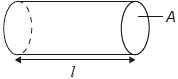
What is the force acting on the area of the cylinder marked A due to the gas?
A.
B.
C.
D.
-
18M.1.SL.TZ1.12:
A sealed cylinder of length l and cross-sectional area A contains N molecules of an ideal gas at kelvin temperature T.

What is the force acting on the area of the cylinder marked A due to the gas?
A.
B.
C.
D.
-
18M.2.HL.TZ1.2b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.2.HL.TZ1.2b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.2.HL.TZ1.b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
- 18M.1.SL.TZ2.13: A sealed container contains water at 5 °C and ice at 0 °C. This system is thermally isolated from...
- 18M.1.SL.TZ2.13: A sealed container contains water at 5 °C and ice at 0 °C. This system is thermally isolated from...
- 18M.1.SL.TZ2.12: A container that contains a fixed mass of an ideal gas is at rest on a truck. The truck now moves...
- 18M.1.SL.TZ2.12: A container that contains a fixed mass of an ideal gas is at rest on a truck. The truck now moves...
-
18M.1.SL.TZ2.11:
The graph shows how the temperature of a liquid varies with time when energy is supplied to the liquid at a constant rate P. The gradient of the graph is K and the liquid has a specific heat capacity c.

What is the mass of the liquid?
A.
B.
C.
D.
-
18M.1.SL.TZ2.11:
The graph shows how the temperature of a liquid varies with time when energy is supplied to the liquid at a constant rate P. The gradient of the graph is K and the liquid has a specific heat capacity c.

What is the mass of the liquid?
A.
B.
C.
D.
-
18M.1.HL.TZ2.9:
Q and R are two rigid containers of volume 3V and V respectively containing molecules of the same ideal gas initially at the same temperature. The gas pressures in Q and R are p and 3p respectively. The containers are connected through a valve of negligible volume that is initially closed.

The valve is opened in such a way that the temperature of the gases does not change. What is the change of pressure in Q?
A. +p
B.
C.
D. –p
-
18M.1.HL.TZ2.9:
Q and R are two rigid containers of volume 3V and V respectively containing molecules of the same ideal gas initially at the same temperature. The gas pressures in Q and R are p and 3p respectively. The containers are connected through a valve of negligible volume that is initially closed.

The valve is opened in such a way that the temperature of the gases does not change. What is the change of pressure in Q?
A. +p
B.
C.
D. –p
-
18M.2.SL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.SL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.SL.TZ2.b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
21N.1.SL.TZ0.11:
A mass of a liquid of specific heat capacity flows every second through a heater of power . What is the difference in temperature between the liquid entering and leaving the heater?
A.B.
C.
D.
-
21N.1.SL.TZ0.11:
A mass of a liquid of specific heat capacity flows every second through a heater of power . What is the difference in temperature between the liquid entering and leaving the heater?
A.B.
C.
D.
-
21N.1.SL.TZ0.12:
A fixed mass of an ideal gas has a volume of , a pressure of p and a temperature of . The gas is compressed to the volume of and its pressure increases to 12p. What is the new temperature of the gas?
A.B.
C.
D.
-
21N.1.SL.TZ0.12:
A fixed mass of an ideal gas has a volume of , a pressure of p and a temperature of . The gas is compressed to the volume of and its pressure increases to 12p. What is the new temperature of the gas?
A.B.
C.
D.
-
21N.1.HL.TZ0.9:
An insulated container of negligible mass contains a mass 2M of a liquid. A piece of a metal of mass M is dropped into the liquid. The temperature of the liquid increases by 10 °C and the temperature of the metal decreases by 80 °C in the same time.
What is ?
A. 2B. 4
C. 8
D. 16
-
21N.1.HL.TZ0.9:
An insulated container of negligible mass contains a mass 2M of a liquid. A piece of a metal of mass M is dropped into the liquid. The temperature of the liquid increases by 10 °C and the temperature of the metal decreases by 80 °C in the same time.
What is ?
A. 2B. 4
C. 8
D. 16
-
21N.1.HL.TZ0.10:
The molar mass of an ideal gas is . A fixed mass of the gas expands at a constant pressure . The graph shows the variation with temperature T of the gas volume V.
What is the gradient of the graph?
A.B.
C.
D.
-
21N.1.HL.TZ0.10:
The molar mass of an ideal gas is . A fixed mass of the gas expands at a constant pressure . The graph shows the variation with temperature T of the gas volume V.
What is the gradient of the graph?
A.B.
C.
D.
-
21N.2.SL.TZ0.2c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.SL.TZ0.2c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.SL.TZ0.c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.SL.TZ0.2b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.SL.TZ0.2b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.SL.TZ0.b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.HL.TZ0.5d.ii:
The mass of the wire is 18 g. The specific heat capacity of copper is 385 J kg−1 K−1. Estimate the increase in temperature of the wire.
-
21N.2.HL.TZ0.5d.ii:
The mass of the wire is 18 g. The specific heat capacity of copper is 385 J kg−1 K−1. Estimate the increase in temperature of the wire.
-
21N.2.HL.TZ0.d.ii:
The mass of the wire is 18 g. The specific heat capacity of copper is 385 J kg−1 K−1. Estimate the increase in temperature of the wire.
-
21N.2.HL.TZ0.6d.i:
Show that the mass of a nitrogen molecule is 4.7 × 10−26 kg.
-
21N.2.HL.TZ0.6d.i:
Show that the mass of a nitrogen molecule is 4.7 × 10−26 kg.
-
21N.2.HL.TZ0.d.i:
Show that the mass of a nitrogen molecule is 4.7 × 10−26 kg.
-
21N.2.HL.TZ0.6d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
21N.2.HL.TZ0.6d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
21N.2.HL.TZ0.d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
18M.2.HL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.HL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.HL.TZ2.a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.HL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ2.b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ2.a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.HL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.HL.TZ1.c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18N.2.SL.TZ0.7a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
-
18N.2.SL.TZ0.7a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
-
18N.2.SL.TZ0.a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.1.SL.TZ0.10: A 700 W electric heater is used to heat 1 kg of water without energy losses. The specific...
- 18N.1.SL.TZ0.10: A 700 W electric heater is used to heat 1 kg of water without energy losses. The specific...
- 18N.1.HL.TZ0.8: A solid substance has just reached its melting point. Thermal energy is supplied to the...
- 18N.1.HL.TZ0.8: A solid substance has just reached its melting point. Thermal energy is supplied to the...
- 18N.2.SL.TZ0.7b.i: Calculate, in kW, the heater power required.
- 18N.2.SL.TZ0.7b.i: Calculate, in kW, the heater power required.
- 18N.2.SL.TZ0.b.i: Calculate, in kW, the heater power required.
- 18N.2.SL.TZ0.7c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.SL.TZ0.7c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.SL.TZ0.c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.HL.TZ0.9c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.HL.TZ0.9c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
- 18N.2.HL.TZ0.c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
-
18N.2.HL.TZ0.9a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
-
18N.2.HL.TZ0.9a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
-
18N.2.HL.TZ0.a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.2.HL.TZ0.9b.i: Calculate, in kW, the heater power required.
- 18N.2.HL.TZ0.9b.i: Calculate, in kW, the heater power required.
- 18N.2.HL.TZ0.b.i: Calculate, in kW, the heater power required.
-
18N.2.HL.TZ0.9b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
-
18N.2.HL.TZ0.9b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
-
18N.2.HL.TZ0.b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
- 22M.1.SL.TZ1.10: A driver uses the brakes on a car to descend a hill at constant speed. What is correct about the...
- 22M.1.SL.TZ1.10: A driver uses the brakes on a car to descend a hill at constant speed. What is correct about the...
-
22M.1.SL.TZ1.11:
Two blocks, X and Y, are placed in contact with each other. Data for the blocks are provided.
X has a mass . What is the mass of Y?
A.
B.
C.
D.
-
22M.1.SL.TZ1.11:
Two blocks, X and Y, are placed in contact with each other. Data for the blocks are provided.
X has a mass . What is the mass of Y?
A.
B.
C.
D.
-
22M.1.SL.TZ1.12:
An ideal gas is maintained at a temperature of 100 K. The variation of the pressure P and of the gas is shown.
What is the quantity of the gas?
A.
B.
C.
D.
-
22M.1.SL.TZ1.12:
An ideal gas is maintained at a temperature of 100 K. The variation of the pressure P and of the gas is shown.
What is the quantity of the gas?
A.
B.
C.
D.
-
22M.2.SL.TZ1.2a:
Estimate the power input to the heating element. State an appropriate unit for your answer.
-
22M.2.SL.TZ1.2a:
Estimate the power input to the heating element. State an appropriate unit for your answer.
-
22M.2.SL.TZ1.a:
Estimate the power input to the heating element. State an appropriate unit for your answer.
-
22M.2.SL.TZ1.2b:
Outline whether your answer to (a) is likely to overestimate or underestimate the power input.
-
22M.2.SL.TZ1.2b:
Outline whether your answer to (a) is likely to overestimate or underestimate the power input.
-
22M.2.SL.TZ1.b:
Outline whether your answer to (a) is likely to overestimate or underestimate the power input.
-
22M.2.SL.TZ1.2c:
Discuss, with reference to the molecules in the liquid, the difference between milk at 11 °C and milk at 84 °C.
-
22M.2.SL.TZ1.2c:
Discuss, with reference to the molecules in the liquid, the difference between milk at 11 °C and milk at 84 °C.
-
22M.2.SL.TZ1.c:
Discuss, with reference to the molecules in the liquid, the difference between milk at 11 °C and milk at 84 °C.
-
22M.2.HL.TZ1.9b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
-
22M.2.HL.TZ1.9b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
-
22M.2.HL.TZ1.b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
- 22M.1.SL.TZ2.12: Which assumption is part of the molecular kinetic model of ideal gases? A. The work done on a...
- 22M.1.SL.TZ2.12: Which assumption is part of the molecular kinetic model of ideal gases? A. The work done on a...
- 22M.1.SL.TZ2.13: System X is at a temperature of 40 °C. Thermal energy is provided to system X until it reaches a...
- 22M.1.SL.TZ2.13: System X is at a temperature of 40 °C. Thermal energy is provided to system X until it reaches a...
-
22M.1.SL.TZ2.10:
A quantity of an ideal gas is at a temperature T in a cylinder with a movable piston that traps a length L of the gas. The piston is moved so that the length of the trapped gas is reduced to and the pressure of the gas doubles.
What is the temperature of the gas at the end of the change?
A.
B.
C.
D. -
22M.1.SL.TZ2.10:
A quantity of an ideal gas is at a temperature T in a cylinder with a movable piston that traps a length L of the gas. The piston is moved so that the length of the trapped gas is reduced to and the pressure of the gas doubles.
What is the temperature of the gas at the end of the change?
A.
B.
C.
D. - 22M.1.SL.TZ2.11: What is true for an ideal gas? A. nRT = NkBT B. nRT = kBT C. RT = NkBT D. RT = kBT
- 22M.1.SL.TZ2.11: What is true for an ideal gas? A. nRT = NkBT B. nRT = kBT C. RT = NkBT D. RT = kBT
- 22M.1.HL.TZ2.11: Water at room temperature is placed in a freezer. The specific heat capacity of water is twice...
- 22M.1.HL.TZ2.11: Water at room temperature is placed in a freezer. The specific heat capacity of water is twice...
-
22M.2.SL.TZ2.2a:
Calculate the number of gas particles in the cylinder.
-
22M.2.SL.TZ2.2a:
Calculate the number of gas particles in the cylinder.
-
22M.2.SL.TZ2.a:
Calculate the number of gas particles in the cylinder.
- 22M.2.SL.TZ2.2b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.2b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.b.i: Discuss, for this process, the changes that occur in the density of the gas.
-
19M.2.HL.TZ2.2ci:
Calculate the ratio .
-
19M.2.HL.TZ2.2ci:
Calculate the ratio .
-
19M.2.HL.TZ2.ci:
Calculate the ratio .
-
19M.2.HL.TZ2.2a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.2a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.2cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
-
19M.2.HL.TZ2.2cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
-
19M.2.HL.TZ2.cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.2.HL.TZ2.dii: Suggest, in terms of conservation of energy, the cause for the above change.
-
19M.2.HL.TZ2.2b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.HL.TZ2.2b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.HL.TZ2.b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.SL.TZ1.4a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.4a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.1.HL.TZ2.14:
Cylinder X has a volume and contains 3.0 mol of an ideal gas. Cylinder Y has a volume and contains 2.0 mol of the same gas.
The gases in X and Y are at the same temperature . The containers are joined by a valve which is opened so that the temperatures do not change.
What is the change in pressure in X?
A.
B.
C.
D.
-
19M.1.HL.TZ2.14:
Cylinder X has a volume and contains 3.0 mol of an ideal gas. Cylinder Y has a volume and contains 2.0 mol of the same gas.
The gases in X and Y are at the same temperature . The containers are joined by a valve which is opened so that the temperatures do not change.
What is the change in pressure in X?
A.
B.
C.
D.
-
19M.2.SL.TZ1.4b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.2.SL.TZ1.4b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.2.SL.TZ1.b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.1.SL.TZ2.12:
A container holds 20 g of argon-40() and 40 g of neon-20 () .
What is in the container?
A. 0.25
B. 0.5
C. 2
D. 4
-
19M.1.SL.TZ2.12:
A container holds 20 g of argon-40() and 40 g of neon-20 () .
What is in the container?
A. 0.25
B. 0.5
C. 2
D. 4
- 19M.1.SL.TZ2.10: A substance changes from the solid phase to the gas phase without becoming a liquid and without a...
- 19M.1.SL.TZ2.10: A substance changes from the solid phase to the gas phase without becoming a liquid and without a...
-
19M.1.HL.TZ2.12:
A liquid of mass m and specific heat capacity c cools. The rate of change of the temperature of the liquid is k. What is the rate at which thermal energy is transferred from the liquid?
A.
B.
C.
D. kmc
-
19M.1.HL.TZ2.12:
A liquid of mass m and specific heat capacity c cools. The rate of change of the temperature of the liquid is k. What is the rate at which thermal energy is transferred from the liquid?
A.
B.
C.
D. kmc
-
19M.2.SL.TZ2.2b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.2b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.b:
Estimate the average speed of the helium atoms in the container.
- 19M.1.SL.TZ1.10: Energy is transferred to water in a flask at a rate P. The water reaches boiling point and then P...
- 19M.1.SL.TZ1.10: Energy is transferred to water in a flask at a rate P. The water reaches boiling point and then P...
-
19M.2.SL.TZ2.2dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
-
19M.2.SL.TZ2.2dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
-
19M.2.SL.TZ2.dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
-
19M.1.SL.TZ2.11:
The temperature of a fixed mass of an ideal gas changes from 200 °C to 400 °C.
What is ?
A. 0.50
B. 0.70
C. 1.4
D. 2.0
-
19M.1.SL.TZ2.11:
The temperature of a fixed mass of an ideal gas changes from 200 °C to 400 °C.
What is ?
A. 0.50
B. 0.70
C. 1.4
D. 2.0
-
19M.2.SL.TZ2.2a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.2a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.2di:
Calculate the ratio .
-
19M.2.SL.TZ2.2di:
Calculate the ratio .
-
19M.2.SL.TZ2.di:
Calculate the ratio .
-
19M.1.SL.TZ1.11:
An insulated tube is filled with a large number n of lead spheres, each of mass m. The tube is inverted s times so that the spheres completely fall through an average distance L each time. The temperature of the spheres is measured before and after the inversions and the resultant change in temperature is ΔT.
What is the specific heat capacity of lead?
A.
B.
C.
D.
-
19M.1.SL.TZ1.11:
An insulated tube is filled with a large number n of lead spheres, each of mass m. The tube is inverted s times so that the spheres completely fall through an average distance L each time. The temperature of the spheres is measured before and after the inversions and the resultant change in temperature is ΔT.
What is the specific heat capacity of lead?
A.
B.
C.
D.
-
19M.2.SL.TZ2.2c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19M.2.SL.TZ2.2c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19M.2.SL.TZ2.c:
Show that the number of helium atoms in the container is about 4 × 1020.
- 19N.1.HL.TZ0.9: Under which conditions of pressure and density will a real gas approximate to an ideal gas?
- 19N.1.HL.TZ0.9: Under which conditions of pressure and density will a real gas approximate to an ideal gas?
-
19N.1.SL.TZ0.9:
A mass of water is at a temperature of 290 K. The specific heat capacity of water is . Ice, at its melting point, is added to the water to reduce the water temperature to the freezing point. The specific latent heat of fusion for ice is . What is the minimum mass of ice that is required?
A.
B.
C.
D.
-
19N.1.SL.TZ0.9:
A mass of water is at a temperature of 290 K. The specific heat capacity of water is . Ice, at its melting point, is added to the water to reduce the water temperature to the freezing point. The specific latent heat of fusion for ice is . What is the minimum mass of ice that is required?
A.
B.
C.
D.
-
19N.1.SL.TZ0.11:
Two flasks P and Q contain an ideal gas and are connected with a tube of negligible volume compared to that of the flasks. The volume of P is twice the volume of Q.
P is held at a temperature of 200 K and Q is held at a temperature of 400 K.
What is mass of ?
A.
B.
C. 4
D. 8
-
19N.1.SL.TZ0.11:
Two flasks P and Q contain an ideal gas and are connected with a tube of negligible volume compared to that of the flasks. The volume of P is twice the volume of Q.
P is held at a temperature of 200 K and Q is held at a temperature of 400 K.
What is mass of ?
A.
B.
C. 4
D. 8
-
19N.2.SL.TZ0.2b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.2b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.b(i):
Determine the pressure of the air inside the refrigerator.
- 19N.1.SL.TZ0.10: An ideal gas is in a closed container. Which changes to its volume and temperature when taken...
- 19N.1.SL.TZ0.10: An ideal gas is in a closed container. Which changes to its volume and temperature when taken...
-
19N.2.SL.TZ0.2b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
-
19N.2.SL.TZ0.2b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
-
19N.2.SL.TZ0.b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
-
19N.2.SL.TZ0.2a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
19N.2.SL.TZ0.2a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
19N.2.SL.TZ0.a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
- 22N.1.SL.TZ0.8: A block of glass of mass 5 kg and temperature 30°C is brought into contact with a block of...
- 22N.1.SL.TZ0.8: A block of glass of mass 5 kg and temperature 30°C is brought into contact with a block of...
-
22N.1.SL.TZ0.10:
Three statements about Boltzmann’s constant kB are:
I. kB has a unit of J K−1
II. kB
III. kB
Which statements are correct?
A. I and II onlyB. I and III only
C. II and III only
D. I, II and III
-
22N.1.SL.TZ0.10:
Three statements about Boltzmann’s constant kB are:
I. kB has a unit of J K−1
II. kB
III. kB
Which statements are correct?
A. I and II onlyB. I and III only
C. II and III only
D. I, II and III
- 22N.1.SL.TZ0.9: A solid mass gains energy at a constant rate until it reaches its liquid phase. The specific heat...
- 22N.1.SL.TZ0.9: A solid mass gains energy at a constant rate until it reaches its liquid phase. The specific heat...
-
22N.1.HL.TZ0.10:
Three samples of the same liquid are mixed in an insulated container. The masses and initial temperatures of the samples are:
What is the equilibrium temperature of the mixture?
A. 45 °CB. 36 °C
C. 30 °C
D. 24 °C
-
22N.1.HL.TZ0.10:
Three samples of the same liquid are mixed in an insulated container. The masses and initial temperatures of the samples are:
What is the equilibrium temperature of the mixture?
A. 45 °CB. 36 °C
C. 30 °C
D. 24 °C
-
22N.1.HL.TZ0.11:
Gases in the atmosphere are compounds of , , and .
Four of these gases are CO2, N2O, CH4 and H2O. A pure sample of each gas is produced. Each sample has the same mass.
Which sample contains the greatest number of molecules?
A. N2OB. H2O
C. CO2
D. CH4
-
22N.1.HL.TZ0.11:
Gases in the atmosphere are compounds of , , and .
Four of these gases are CO2, N2O, CH4 and H2O. A pure sample of each gas is produced. Each sample has the same mass.
Which sample contains the greatest number of molecules?
A. N2OB. H2O
C. CO2
D. CH4
-
22N.2.SL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.SL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.SL.TZ0.a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
- 22N.2.HL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.HL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.HL.TZ0.b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.HL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.HL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.HL.TZ0.b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 17N.1.SL.TZ0.9: What does the constant n represent in the equation of state for an ideal gas pV = nRT? A. The...
- 17N.1.SL.TZ0.9: What does the constant n represent in the equation of state for an ideal gas pV = nRT? A. The...
- 17N.1.HL.TZ0.9: The fraction of the internal energy that is due to molecular vibration varies in the different...
- 17N.1.HL.TZ0.9: The fraction of the internal energy that is due to molecular vibration varies in the different...
-
17N.3.SL.TZ0.1b.ii:
State the unit for the quantity represented by the gradient in your answer to (b)(i).
-
17N.3.SL.TZ0.1b.ii:
State the unit for the quantity represented by the gradient in your answer to (b)(i).
-
17N.3.SL.TZ0.b.ii:
State the unit for the quantity represented by the gradient in your answer to (b)(i).
-
18M.2.SL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.a.i:
State what is meant by an ideal gas.
-
18N.1.SL.TZ0.11:
A container is filled with a mixture of helium and oxygen at the same temperature. The molar mass of helium is 4 g mol–1 and that of oxygen is 32 g mol–1.
What is the ratio ?
A.
B.
C.
D. 8
-
18N.1.SL.TZ0.11:
A container is filled with a mixture of helium and oxygen at the same temperature. The molar mass of helium is 4 g mol–1 and that of oxygen is 32 g mol–1.
What is the ratio ?
A.
B.
C.
D. 8
-
18N.1.SL.TZ0.12:
Container X contains 1.0 mol of an ideal gas. Container Y contains 2.0 mol of the ideal gas. Y has four times the volume of X. The pressure in X is twice that in Y.
What is ?
A.
B.
C. 1
D. 2
-
18N.1.SL.TZ0.12:
Container X contains 1.0 mol of an ideal gas. Container Y contains 2.0 mol of the ideal gas. Y has four times the volume of X. The pressure in X is twice that in Y.
What is ?
A.
B.
C. 1
D. 2
-
18N.2.SL.TZ0.7b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
-
18N.2.SL.TZ0.7b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
-
18N.2.SL.TZ0.b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
- 19M.1.SL.TZ1.12: Boiling water is heated in a 2 kW electric kettle. The initial mass of water is 0.4 kg. Assume...
- 19M.1.SL.TZ1.12: Boiling water is heated in a 2 kW electric kettle. The initial mass of water is 0.4 kg. Assume...
-
19M.1.SL.TZ1.13:
A gas storage tank of fixed volume V contains N molecules of an ideal gas at temperature T. The pressure at kelvin temperature T is 20 MPa. molecules are removed and the temperature changed to 2T. What is the new pressure of the gas?
A. 10 MPa
B. 15 MPa
C. 30 MPa
D. 40 MPa
-
19M.1.SL.TZ1.13:
A gas storage tank of fixed volume V contains N molecules of an ideal gas at temperature T. The pressure at kelvin temperature T is 20 MPa. molecules are removed and the temperature changed to 2T. What is the new pressure of the gas?
A. 10 MPa
B. 15 MPa
C. 30 MPa
D. 40 MPa
-
19M.2.SL.TZ1.4b.ii:
Determine the atmospheric pressure. Give a suitable unit for your answer.
-
19M.2.SL.TZ1.4b.ii:
Determine the atmospheric pressure. Give a suitable unit for your answer.
-
19M.2.SL.TZ1.b.ii:
Determine the atmospheric pressure. Give a suitable unit for your answer.
-
20N.1.HL.TZ0.9:
Two containers X and Y are maintained at the same temperature. X has volume and Y has volume . They both hold an ideal gas. The pressure in X is and the pressure in Y is . The containers are then joined by a tube of negligible volume. What is the final pressure in the containers?
A.
B.
C.
D.
-
20N.1.HL.TZ0.9:
Two containers X and Y are maintained at the same temperature. X has volume and Y has volume . They both hold an ideal gas. The pressure in X is and the pressure in Y is . The containers are then joined by a tube of negligible volume. What is the final pressure in the containers?
A.
B.
C.
D.
-
20N.2.SL.TZ0.3c:
Calculate the mass of the oil that remains unfrozen after minutes.
-
20N.2.SL.TZ0.3c:
Calculate the mass of the oil that remains unfrozen after minutes.
-
20N.2.SL.TZ0.c:
Calculate the mass of the oil that remains unfrozen after minutes.
-
21M.2.SL.TZ2.2a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.2a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.2b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.2b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.2c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
-
21M.2.SL.TZ2.2c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
-
21M.2.SL.TZ2.c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
-
21M.1.SL.TZ2.10:
A sample of oxygen gas with a volume of is at . The gas is heated so that it expands at a constant pressure to a final volume of . What is the final temperature of the gas?
A.
B.
C.
D.
-
21M.1.SL.TZ2.10:
A sample of oxygen gas with a volume of is at . The gas is heated so that it expands at a constant pressure to a final volume of . What is the final temperature of the gas?
A.
B.
C.
D.
- 21N.1.SL.TZ0.10: A liquid is vaporized to a gas at a constant temperature. Three quantities of the substance are...
- 21N.1.SL.TZ0.10: A liquid is vaporized to a gas at a constant temperature. Three quantities of the substance are...
- 21N.2.SL.TZ0.2a: State what is meant by the internal energy of an ideal gas.
- 21N.2.SL.TZ0.2a: State what is meant by the internal energy of an ideal gas.
- 21N.2.SL.TZ0.a: State what is meant by the internal energy of an ideal gas.
-
21N.2.SL.TZ0.2b.i:
Calculate the pressure of the gas.
-
21N.2.SL.TZ0.2b.i:
Calculate the pressure of the gas.
-
21N.2.SL.TZ0.b.i:
Calculate the pressure of the gas.
-
21N.2.HL.TZ0.4c.i:
Estimate the power, in kW, that is available from the plutonium at launch.
-
21N.2.HL.TZ0.4c.i:
Estimate the power, in kW, that is available from the plutonium at launch.
-
21N.2.HL.TZ0.c.i:
Estimate the power, in kW, that is available from the plutonium at launch.
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22M.2.SL.TZ2.b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22N.2.SL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.SL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
- 22N.2.SL.TZ0.b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.SL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.SL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.SL.TZ0.b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
-
22N.2.HL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.HL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.HL.TZ0.a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
23M.1.HL.TZ1.25:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.29:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.29:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.HL.TZ1.25:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.30:
Light of intensity 500 W m−2 is incident on concrete and on snow. 300 W m−2 is reflected from the
concrete and 400 W m−2 is reflected from the snow.What is ?
A.B.
C.
D. 2
-
23M.1.SL.TZ1.30:
Light of intensity 500 W m−2 is incident on concrete and on snow. 300 W m−2 is reflected from the
concrete and 400 W m−2 is reflected from the snow.What is ?
A.B.
C.
D. 2
- 23M.1.SL.TZ2.12: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.10: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.SL.TZ2.12: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.10: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.9: A fixed mass of an ideal gas expands slowly at constant temperature in a container. Three...
- 23M.1.HL.TZ2.9: A fixed mass of an ideal gas expands slowly at constant temperature in a container. Three...
-
23M.1.SL.TZ2.11:
A vessel contains a mass X of helium gas and a mass 2X of oxygen gas.
Molar mass of helium = 4 g
Molar mass of oxygen = 32 g
What is the ?
A.B.
C. 4
D. 8
-
23M.1.SL.TZ2.11:
A vessel contains a mass X of helium gas and a mass 2X of oxygen gas.
Molar mass of helium = 4 g
Molar mass of oxygen = 32 g
What is the ?
A.B.
C. 4
D. 8
- 23M.2.SL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.HL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.HL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.HL.TZ2.a: State the unit for pV in fundamental SI units.
- 23M.2.SL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.SL.TZ2.a: State the unit for pV in fundamental SI units.
- 23M.1.HL.TZ2.27: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
- 23M.1.HL.TZ2.27: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
-
23M.1.HL.TZ2.33:
An ac generator produces a root mean square (rms) voltage V. What is the peak output voltage when the frequency is doubled?
A.B.
C.
D.
-
23M.1.HL.TZ2.33:
An ac generator produces a root mean square (rms) voltage V. What is the peak output voltage when the frequency is doubled?
A.B.
C.
D.
- 23M.1.SL.TZ2.30: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
- 23M.1.SL.TZ2.30: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
Sub sections and their related questions
3.1 – Thermal concepts
- 17N.1.SL.TZ0.10: A 1.0 kW heater supplies energy to a liquid of mass 0.50 kg. The temperature of the liquid...
- 17N.1.HL.TZ0.9: The fraction of the internal energy that is due to molecular vibration varies in the different...
-
17N.2.SL.TZ0.4b.i:
Determine the energy required to melt all of the ice from –20 °C to water at a temperature of 0 °C.
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3 -
17N.2.SL.TZ0.4b.ii:
Outline the difference between the molecular structure of a solid and a liquid.
- 17N.3.SL.TZ0.1b.i: Determine the gradient of the line at a temperature of 80 °C.
-
17N.3.SL.TZ0.1b.ii:
State the unit for the quantity represented by the gradient in your answer to (b)(i).
- 17N.3.SL.TZ0.1c.i: Calculate the energy required to raise the temperature of the water from 75 °C to 85 °C.
-
17N.3.SL.TZ0.1c.ii:
Using an appropriate error calculation, justify the number of significant figures that should be used for your answer to (c)(i).
-
18M.1.SL.TZ1.11:
What are the units of the ratio ?
A. no units
B. k
C. k–1
D. k–2
-
18M.2.SL.TZ1.2b.i:
Calculate, in kg, the mass of the gas.
-
18M.1.SL.TZ2.11:
The graph shows how the temperature of a liquid varies with time when energy is supplied to the liquid at a constant rate P. The gradient of the graph is K and the liquid has a specific heat capacity c.

What is the mass of the liquid?
A.
B.
C.
D.
- 18M.1.SL.TZ2.12: A container that contains a fixed mass of an ideal gas is at rest on a truck. The truck now moves...
- 18M.1.SL.TZ2.13: A sealed container contains water at 5 °C and ice at 0 °C. This system is thermally isolated from...
- 18N.1.SL.TZ0.10: A 700 W electric heater is used to heat 1 kg of water without energy losses. The specific...
- 18N.1.HL.TZ0.8: A solid substance has just reached its melting point. Thermal energy is supplied to the...
-
18N.2.SL.TZ0.7a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.2.SL.TZ0.7b.i: Calculate, in kW, the heater power required.
-
18N.2.HL.TZ0.9a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.2.HL.TZ0.9b.i: Calculate, in kW, the heater power required.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.1.SL.TZ1.10: Energy is transferred to water in a flask at a rate P. The water reaches boiling point and then P...
-
19M.1.SL.TZ1.11:
An insulated tube is filled with a large number n of lead spheres, each of mass m. The tube is inverted s times so that the spheres completely fall through an average distance L each time. The temperature of the spheres is measured before and after the inversions and the resultant change in temperature is ΔT.
What is the specific heat capacity of lead?
A.
B.
C.
D.
- 19M.1.SL.TZ1.12: Boiling water is heated in a 2 kW electric kettle. The initial mass of water is 0.4 kg. Assume...
-
19M.2.SL.TZ1.4b.ii:
Determine the atmospheric pressure. Give a suitable unit for your answer.
- 19M.1.SL.TZ2.10: A substance changes from the solid phase to the gas phase without becoming a liquid and without a...
-
19M.1.HL.TZ2.12:
A liquid of mass m and specific heat capacity c cools. The rate of change of the temperature of the liquid is k. What is the rate at which thermal energy is transferred from the liquid?
A.
B.
C.
D. kmc
-
19N.1.SL.TZ0.9:
A mass of water is at a temperature of 290 K. The specific heat capacity of water is . Ice, at its melting point, is added to the water to reduce the water temperature to the freezing point. The specific latent heat of fusion for ice is . What is the minimum mass of ice that is required?
A.
B.
C.
D.
-
20N.1.SL.TZ0.13:
A bicycle of mass comes to rest from speed using the back brake. The brake has a specific heat capacity of and a mass . Half of the kinetic energy is absorbed by the brake.
What is the change in temperature of the brake?
A.
B.
C.
D.
-
20N.2.SL.TZ0.3a(i):
Calculate the thermal energy transferred from the sample during the first minutes.
-
20N.2.SL.TZ0.3a(ii):
Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer.
- 20N.2.SL.TZ0.3b: The sample begins to freeze during the thermal energy transfer. Explain, in terms of the...
-
20N.2.SL.TZ0.3c:
Calculate the mass of the oil that remains unfrozen after minutes.
-
21M.2.SL.TZ1.3b.i:
Estimate the specific latent heat of vaporization of water. State an appropriate unit for your answer.
- 21M.2.SL.TZ1.3b.ii: Explain why the temperature of water remains at 100 °C during this time.
-
21M.2.SL.TZ1.3c:
The heater is removed and a mass of 0.30 kg of pasta at −10 °C is added to the boiling water.
Determine the equilibrium temperature of the pasta and water after the pasta is added. Other heat transfers are negligible.
Specific heat capacity of pasta = 1.8 kJ kg−1 K−1
Specific heat capacity of water = 4.2 kJ kg−1 K−1 -
21M.1.SL.TZ1.11:
When 40 kJ of energy is transferred to a quantity of a liquid substance, its temperature increases by 20 K. When 600 kJ of energy is transferred to the same quantity of the liquid at its boiling temperature, it vaporizes completely at constant temperature. What is
for this substance?
A. 15 K−1
B. 15 K
C. 300 K−1
D. 300 K
-
21M.1.SL.TZ2.12:
A piece of metal at a temperature of is dropped into an equal mass of water at a temperature of in a container of negligible mass. The specific heat capacity of water is four times that of the metal. What is the final temperature of the mixture?
A.
B.
C.
D.
- 21N.1.SL.TZ0.10: A liquid is vaporized to a gas at a constant temperature. Three quantities of the substance are...
-
21N.1.SL.TZ0.11:
A mass of a liquid of specific heat capacity flows every second through a heater of power . What is the difference in temperature between the liquid entering and leaving the heater?
A.B.
C.
D.
-
21N.1.HL.TZ0.9:
An insulated container of negligible mass contains a mass 2M of a liquid. A piece of a metal of mass M is dropped into the liquid. The temperature of the liquid increases by 10 °C and the temperature of the metal decreases by 80 °C in the same time.
What is ?
A. 2B. 4
C. 8
D. 16
- 21N.2.SL.TZ0.2a: State what is meant by the internal energy of an ideal gas.
-
21N.2.HL.TZ0.4c.i:
Estimate the power, in kW, that is available from the plutonium at launch.
-
21N.2.HL.TZ0.5d.ii:
The mass of the wire is 18 g. The specific heat capacity of copper is 385 J kg−1 K−1. Estimate the increase in temperature of the wire.
-
21N.2.HL.TZ0.6d.i:
Show that the mass of a nitrogen molecule is 4.7 × 10−26 kg.
- 22M.1.SL.TZ2.13: System X is at a temperature of 40 °C. Thermal energy is provided to system X until it reaches a...
- 22M.1.HL.TZ2.11: Water at room temperature is placed in a freezer. The specific heat capacity of water is twice...
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22M.1.SL.TZ1.10: A driver uses the brakes on a car to descend a hill at constant speed. What is correct about the...
-
22M.1.SL.TZ1.11:
Two blocks, X and Y, are placed in contact with each other. Data for the blocks are provided.
X has a mass . What is the mass of Y?
A.
B.
C.
D.
-
22M.2.SL.TZ1.2a:
Estimate the power input to the heating element. State an appropriate unit for your answer.
-
22M.2.SL.TZ1.2b:
Outline whether your answer to (a) is likely to overestimate or underestimate the power input.
-
22M.2.SL.TZ1.2c:
Discuss, with reference to the molecules in the liquid, the difference between milk at 11 °C and milk at 84 °C.
- 22N.1.SL.TZ0.8: A block of glass of mass 5 kg and temperature 30°C is brought into contact with a block of...
- 22N.1.SL.TZ0.9: A solid mass gains energy at a constant rate until it reaches its liquid phase. The specific heat...
-
22N.1.HL.TZ0.10:
Three samples of the same liquid are mixed in an insulated container. The masses and initial temperatures of the samples are:
What is the equilibrium temperature of the mixture?
A. 45 °CB. 36 °C
C. 30 °C
D. 24 °C
-
22N.2.SL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.HL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
23M.1.HL.TZ2.33:
An ac generator produces a root mean square (rms) voltage V. What is the peak output voltage when the frequency is doubled?
A.B.
C.
D.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.2.HL.TZ2.dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.1.SL.TZ1.10: Energy is transferred to water in a flask at a rate P. The water reaches boiling point and then P...
-
19M.1.SL.TZ1.11:
An insulated tube is filled with a large number n of lead spheres, each of mass m. The tube is inverted s times so that the spheres completely fall through an average distance L each time. The temperature of the spheres is measured before and after the inversions and the resultant change in temperature is ΔT.
What is the specific heat capacity of lead?
A.
B.
C.
D.
- 19M.1.SL.TZ1.12: Boiling water is heated in a 2 kW electric kettle. The initial mass of water is 0.4 kg. Assume...
-
19M.2.SL.TZ1.4b.ii:
Determine the atmospheric pressure. Give a suitable unit for your answer.
-
19M.2.SL.TZ1.b.ii:
Determine the atmospheric pressure. Give a suitable unit for your answer.
- 19M.1.SL.TZ2.10: A substance changes from the solid phase to the gas phase without becoming a liquid and without a...
-
19M.1.HL.TZ2.12:
A liquid of mass m and specific heat capacity c cools. The rate of change of the temperature of the liquid is k. What is the rate at which thermal energy is transferred from the liquid?
A.
B.
C.
D. kmc
-
19N.1.SL.TZ0.9:
A mass of water is at a temperature of 290 K. The specific heat capacity of water is . Ice, at its melting point, is added to the water to reduce the water temperature to the freezing point. The specific latent heat of fusion for ice is . What is the minimum mass of ice that is required?
A.
B.
C.
D.
-
20N.1.SL.TZ0.13:
A bicycle of mass comes to rest from speed using the back brake. The brake has a specific heat capacity of and a mass . Half of the kinetic energy is absorbed by the brake.
What is the change in temperature of the brake?
A.
B.
C.
D.
-
20N.2.SL.TZ0.3a(i):
Calculate the thermal energy transferred from the sample during the first minutes.
-
20N.2.SL.TZ0.3a(ii):
Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer.
- 20N.2.SL.TZ0.3b: The sample begins to freeze during the thermal energy transfer. Explain, in terms of the...
-
20N.2.SL.TZ0.3c:
Calculate the mass of the oil that remains unfrozen after minutes.
-
20N.2.SL.TZ0.a(i):
Calculate the thermal energy transferred from the sample during the first minutes.
-
20N.2.SL.TZ0.a(ii):
Estimate the specific heat capacity of the oil in its liquid phase. State an appropriate unit for your answer.
- 20N.2.SL.TZ0.b: The sample begins to freeze during the thermal energy transfer. Explain, in terms of the...
-
20N.2.SL.TZ0.c:
Calculate the mass of the oil that remains unfrozen after minutes.
-
21M.2.SL.TZ1.3b.i:
Estimate the specific latent heat of vaporization of water. State an appropriate unit for your answer.
- 21M.2.SL.TZ1.3b.ii: Explain why the temperature of water remains at 100 °C during this time.
-
21M.2.SL.TZ1.3c:
The heater is removed and a mass of 0.30 kg of pasta at −10 °C is added to the boiling water.
Determine the equilibrium temperature of the pasta and water after the pasta is added. Other heat transfers are negligible.
Specific heat capacity of pasta = 1.8 kJ kg−1 K−1
Specific heat capacity of water = 4.2 kJ kg−1 K−1 -
21M.2.SL.TZ1.b.i:
Estimate the specific latent heat of vaporization of water. State an appropriate unit for your answer.
- 21M.2.SL.TZ1.b.ii: Explain why the temperature of water remains at 100 °C during this time.
-
21M.2.SL.TZ1.c:
The heater is removed and a mass of 0.30 kg of pasta at −10 °C is added to the boiling water.
Determine the equilibrium temperature of the pasta and water after the pasta is added. Other heat transfers are negligible.
Specific heat capacity of pasta = 1.8 kJ kg−1 K−1
Specific heat capacity of water = 4.2 kJ kg−1 K−1 -
21M.1.SL.TZ1.11:
When 40 kJ of energy is transferred to a quantity of a liquid substance, its temperature increases by 20 K. When 600 kJ of energy is transferred to the same quantity of the liquid at its boiling temperature, it vaporizes completely at constant temperature. What is
for this substance?
A. 15 K−1
B. 15 K
C. 300 K−1
D. 300 K
-
21M.1.SL.TZ2.12:
A piece of metal at a temperature of is dropped into an equal mass of water at a temperature of in a container of negligible mass. The specific heat capacity of water is four times that of the metal. What is the final temperature of the mixture?
A.
B.
C.
D.
- 21N.1.SL.TZ0.10: A liquid is vaporized to a gas at a constant temperature. Three quantities of the substance are...
-
21N.1.SL.TZ0.11:
A mass of a liquid of specific heat capacity flows every second through a heater of power . What is the difference in temperature between the liquid entering and leaving the heater?
A.B.
C.
D.
-
21N.1.HL.TZ0.9:
An insulated container of negligible mass contains a mass 2M of a liquid. A piece of a metal of mass M is dropped into the liquid. The temperature of the liquid increases by 10 °C and the temperature of the metal decreases by 80 °C in the same time.
What is ?
A. 2B. 4
C. 8
D. 16
- 21N.2.SL.TZ0.2a: State what is meant by the internal energy of an ideal gas.
- 21N.2.SL.TZ0.a: State what is meant by the internal energy of an ideal gas.
-
21N.2.HL.TZ0.4c.i:
Estimate the power, in kW, that is available from the plutonium at launch.
-
21N.2.HL.TZ0.c.i:
Estimate the power, in kW, that is available from the plutonium at launch.
-
21N.2.HL.TZ0.5d.ii:
The mass of the wire is 18 g. The specific heat capacity of copper is 385 J kg−1 K−1. Estimate the increase in temperature of the wire.
-
21N.2.HL.TZ0.d.ii:
The mass of the wire is 18 g. The specific heat capacity of copper is 385 J kg−1 K−1. Estimate the increase in temperature of the wire.
-
21N.2.HL.TZ0.6d.i:
Show that the mass of a nitrogen molecule is 4.7 × 10−26 kg.
-
21N.2.HL.TZ0.d.i:
Show that the mass of a nitrogen molecule is 4.7 × 10−26 kg.
- 22M.1.SL.TZ2.13: System X is at a temperature of 40 °C. Thermal energy is provided to system X until it reaches a...
- 22M.1.HL.TZ2.11: Water at room temperature is placed in a freezer. The specific heat capacity of water is twice...
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22M.2.SL.TZ2.b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
- 22M.1.SL.TZ1.10: A driver uses the brakes on a car to descend a hill at constant speed. What is correct about the...
-
22M.1.SL.TZ1.11:
Two blocks, X and Y, are placed in contact with each other. Data for the blocks are provided.
X has a mass . What is the mass of Y?
A.
B.
C.
D.
-
22M.2.SL.TZ1.2a:
Estimate the power input to the heating element. State an appropriate unit for your answer.
-
22M.2.SL.TZ1.2b:
Outline whether your answer to (a) is likely to overestimate or underestimate the power input.
-
22M.2.SL.TZ1.2c:
Discuss, with reference to the molecules in the liquid, the difference between milk at 11 °C and milk at 84 °C.
-
22M.2.SL.TZ1.a:
Estimate the power input to the heating element. State an appropriate unit for your answer.
-
22M.2.SL.TZ1.b:
Outline whether your answer to (a) is likely to overestimate or underestimate the power input.
-
22M.2.SL.TZ1.c:
Discuss, with reference to the molecules in the liquid, the difference between milk at 11 °C and milk at 84 °C.
- 22N.1.SL.TZ0.8: A block of glass of mass 5 kg and temperature 30°C is brought into contact with a block of...
- 22N.1.SL.TZ0.9: A solid mass gains energy at a constant rate until it reaches its liquid phase. The specific heat...
-
22N.1.HL.TZ0.10:
Three samples of the same liquid are mixed in an insulated container. The masses and initial temperatures of the samples are:
What is the equilibrium temperature of the mixture?
A. 45 °CB. 36 °C
C. 30 °C
D. 24 °C
-
22N.2.SL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.SL.TZ0.a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.HL.TZ0.2a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
-
22N.2.HL.TZ0.a.i:
Determine the minimum area of the solar heating panel required to increase the temperature of all the water in the tank to 30°C during a time of 1.0 hour.
- 17N.1.SL.TZ0.10: A 1.0 kW heater supplies energy to a liquid of mass 0.50 kg. The temperature of the liquid...
- 17N.1.HL.TZ0.9: The fraction of the internal energy that is due to molecular vibration varies in the different...
-
17N.2.SL.TZ0.4b.i:
Determine the energy required to melt all of the ice from –20 °C to water at a temperature of 0 °C.
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3 -
17N.2.SL.TZ0.4b.ii:
Outline the difference between the molecular structure of a solid and a liquid.
-
17N.2.SL.TZ0.b.i:
Determine the energy required to melt all of the ice from –20 °C to water at a temperature of 0 °C.
Specific latent heat of fusion of ice = 330 kJ kg–1
Specific heat capacity of ice = 2.1 kJ kg–1 k–1
Density of ice = 920 kg m–3 -
17N.2.SL.TZ0.b.ii:
Outline the difference between the molecular structure of a solid and a liquid.
- 17N.3.SL.TZ0.1b.i: Determine the gradient of the line at a temperature of 80 °C.
-
17N.3.SL.TZ0.1b.ii:
State the unit for the quantity represented by the gradient in your answer to (b)(i).
- 17N.3.SL.TZ0.1c.i: Calculate the energy required to raise the temperature of the water from 75 °C to 85 °C.
-
17N.3.SL.TZ0.1c.ii:
Using an appropriate error calculation, justify the number of significant figures that should be used for your answer to (c)(i).
- 17N.3.SL.TZ0.b.i: Determine the gradient of the line at a temperature of 80 °C.
-
17N.3.SL.TZ0.b.ii:
State the unit for the quantity represented by the gradient in your answer to (b)(i).
- 17N.3.SL.TZ0.c.i: Calculate the energy required to raise the temperature of the water from 75 °C to 85 °C.
-
17N.3.SL.TZ0.c.ii:
Using an appropriate error calculation, justify the number of significant figures that should be used for your answer to (c)(i).
-
23M.1.HL.TZ2.33:
An ac generator produces a root mean square (rms) voltage V. What is the peak output voltage when the frequency is doubled?
A.B.
C.
D.
-
18M.1.SL.TZ1.11:
What are the units of the ratio ?
A. no units
B. k
C. k–1
D. k–2
-
18M.2.SL.TZ1.2b.i:
Calculate, in kg, the mass of the gas.
-
18M.2.SL.TZ1.b.i:
Calculate, in kg, the mass of the gas.
-
18M.1.SL.TZ2.11:
The graph shows how the temperature of a liquid varies with time when energy is supplied to the liquid at a constant rate P. The gradient of the graph is K and the liquid has a specific heat capacity c.

What is the mass of the liquid?
A.
B.
C.
D.
- 18M.1.SL.TZ2.12: A container that contains a fixed mass of an ideal gas is at rest on a truck. The truck now moves...
- 18M.1.SL.TZ2.13: A sealed container contains water at 5 °C and ice at 0 °C. This system is thermally isolated from...
- 18N.1.SL.TZ0.10: A 700 W electric heater is used to heat 1 kg of water without energy losses. The specific...
- 18N.1.HL.TZ0.8: A solid substance has just reached its melting point. Thermal energy is supplied to the...
-
18N.2.SL.TZ0.7a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.2.SL.TZ0.7b.i: Calculate, in kW, the heater power required.
-
18N.2.SL.TZ0.a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.2.SL.TZ0.b.i: Calculate, in kW, the heater power required.
-
18N.2.HL.TZ0.9a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.2.HL.TZ0.9b.i: Calculate, in kW, the heater power required.
-
18N.2.HL.TZ0.a:
Distinguish between the internal energy of the oxygen at the boiling point when it is in its liquid phase and when it is in its gas phase.
- 18N.2.HL.TZ0.b.i: Calculate, in kW, the heater power required.
3.2 – Modelling a gas
- 17N.1.SL.TZ0.9: What does the constant n represent in the equation of state for an ideal gas pV = nRT? A. The...
- 17N.1.SL.TZ0.11: Under what conditions of pressure and temperature does a real gas approximate to an ideal gas?
-
17N.1.HL.TZ0.12:
Unpolarized light of intensity I0 is incident on a polarizing filter. Light from this filter is incident on a second filter, which has its axis of polarization at 30˚ to that of the first filter.
The value of cos 30˚ is . What is the intensity of the light emerging through the second filter?
A. I0
B. I0
C. I0
D. I0
- 18M.1.SL.TZ1.10: A fixed mass of an ideal gas is trapped in a cylinder of constant volume and its temperature is...
-
18M.1.SL.TZ1.12:
A sealed cylinder of length l and cross-sectional area A contains N molecules of an ideal gas at kelvin temperature T.

What is the force acting on the area of the cylinder marked A due to the gas?
A.
B.
C.
D.
-
18M.2.SL.TZ1.2a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ1.2b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.2.HL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.1.HL.TZ2.9:
Q and R are two rigid containers of volume 3V and V respectively containing molecules of the same ideal gas initially at the same temperature. The gas pressures in Q and R are p and 3p respectively. The containers are connected through a valve of negligible volume that is initially closed.

The valve is opened in such a way that the temperature of the gases does not change. What is the change of pressure in Q?
A. +p
B.
C.
D. –p
-
18M.2.HL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.HL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18N.1.SL.TZ0.11:
A container is filled with a mixture of helium and oxygen at the same temperature. The molar mass of helium is 4 g mol–1 and that of oxygen is 32 g mol–1.
What is the ratio ?
A.
B.
C.
D. 8
-
18N.1.SL.TZ0.12:
Container X contains 1.0 mol of an ideal gas. Container Y contains 2.0 mol of the ideal gas. Y has four times the volume of X. The pressure in X is twice that in Y.
What is ?
A.
B.
C. 1
D. 2
-
18N.2.SL.TZ0.7b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
- 18N.2.SL.TZ0.7c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
-
18N.2.HL.TZ0.9b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
- 18N.2.HL.TZ0.9c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
-
19M.2.HL.TZ2.2a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.2b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.HL.TZ2.2ci:
Calculate the ratio .
-
19M.2.HL.TZ2.2cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
-
19M.1.SL.TZ1.13:
A gas storage tank of fixed volume V contains N molecules of an ideal gas at temperature T. The pressure at kelvin temperature T is 20 MPa. molecules are removed and the temperature changed to 2T. What is the new pressure of the gas?
A. 10 MPa
B. 15 MPa
C. 30 MPa
D. 40 MPa
-
19M.2.SL.TZ1.4a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.4b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.1.HL.TZ2.14:
Cylinder X has a volume and contains 3.0 mol of an ideal gas. Cylinder Y has a volume and contains 2.0 mol of the same gas.
The gases in X and Y are at the same temperature . The containers are joined by a valve which is opened so that the temperatures do not change.
What is the change in pressure in X?
A.
B.
C.
D.
-
19M.1.SL.TZ2.12:
A container holds 20 g of argon-40() and 40 g of neon-20 () .
What is in the container?
A. 0.25
B. 0.5
C. 2
D. 4
-
19M.1.SL.TZ2.11:
The temperature of a fixed mass of an ideal gas changes from 200 °C to 400 °C.
What is ?
A. 0.50
B. 0.70
C. 1.4
D. 2.0
-
19M.2.SL.TZ2.2a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.2b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.2c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19M.2.SL.TZ2.2di:
Calculate the ratio .
-
19M.2.SL.TZ2.2dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
- 19N.1.SL.TZ0.10: An ideal gas is in a closed container. Which changes to its volume and temperature when taken...
-
19N.1.SL.TZ0.11:
Two flasks P and Q contain an ideal gas and are connected with a tube of negligible volume compared to that of the flasks. The volume of P is twice the volume of Q.
P is held at a temperature of 200 K and Q is held at a temperature of 400 K.
What is mass of ?
A.
B.
C. 4
D. 8
- 19N.1.HL.TZ0.9: Under which conditions of pressure and density will a real gas approximate to an ideal gas?
-
19N.2.SL.TZ0.2a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
19N.2.SL.TZ0.2b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.2b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
- 20N.1.SL.TZ0.11: An ideal gas of constant mass is heated in a container of constant volume. What is the reason...
-
20N.1.SL.TZ0.12:
A substance in the gas state has a density about times less than when it is in the liquid state. The diameter of a molecule is . What is the best estimate of the average distance between molecules in the gas state?
A.
B.
C.
D.
- 20N.1.HL.TZ0.7: What is not an assumption of the kinetic model of an ideal gas? A. Attractive forces between...
-
20N.1.HL.TZ0.9:
Two containers X and Y are maintained at the same temperature. X has volume and Y has volume . They both hold an ideal gas. The pressure in X is and the pressure in Y is . The containers are then joined by a tube of negligible volume. What is the final pressure in the containers?
A.
B.
C.
D.
-
21M.2.SL.TZ1.3a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
- 21M.2.SL.TZ1.3a.ii: State one assumption of the kinetic model of an ideal gas.
-
21M.2.SL.TZ2.2a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.2b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.2c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
- 21M.1.SL.TZ1.10: Which aspect of thermal physics is best explained by the molecular kinetic model? A. The...
- 21M.1.HL.TZ1.10: Two ideal gases X and Y are at the same temperature. The mass of a particle of gas X is larger...
- 21M.1.SL.TZ1.25: What is the relation between the value of the unified atomic mass unit in grams and the value of...
- 21M.1.SL.TZ1.12: A quantity of 2.00 mol of an ideal gas is maintained at a temperature of 127 ºC in a container of...
-
21M.1.SL.TZ2.10:
A sample of oxygen gas with a volume of is at . The gas is heated so that it expands at a constant pressure to a final volume of . What is the final temperature of the gas?
A.
B.
C.
D.
-
21M.1.SL.TZ2.11:
Two identical containers X and Y each contain an ideal gas. X has N molecules of gas at an absolute temperature of T and Y has 3N molecules of gas at an absolute temperature of What is the ratio of the pressures ?
A.
B.
C.
D.
-
21N.1.SL.TZ0.12:
A fixed mass of an ideal gas has a volume of , a pressure of p and a temperature of . The gas is compressed to the volume of and its pressure increases to 12p. What is the new temperature of the gas?
A.B.
C.
D.
-
21N.1.HL.TZ0.10:
The molar mass of an ideal gas is . A fixed mass of the gas expands at a constant pressure . The graph shows the variation with temperature T of the gas volume V.
What is the gradient of the graph?
A.B.
C.
D.
-
21N.2.SL.TZ0.2b.i:
Calculate the pressure of the gas.
-
21N.2.SL.TZ0.2b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.SL.TZ0.2c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.HL.TZ0.6d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
22M.1.SL.TZ2.10:
A quantity of an ideal gas is at a temperature T in a cylinder with a movable piston that traps a length L of the gas. The piston is moved so that the length of the trapped gas is reduced to and the pressure of the gas doubles.
What is the temperature of the gas at the end of the change?
A.
B.
C.
D. - 22M.1.SL.TZ2.11: What is true for an ideal gas? A. nRT = NkBT B. nRT = kBT C. RT = NkBT D. RT = kBT
- 22M.1.SL.TZ2.12: Which assumption is part of the molecular kinetic model of ideal gases? A. The work done on a...
-
22M.2.SL.TZ2.2a:
Calculate the number of gas particles in the cylinder.
- 22M.2.SL.TZ2.2b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
-
22M.1.SL.TZ1.12:
An ideal gas is maintained at a temperature of 100 K. The variation of the pressure P and of the gas is shown.
What is the quantity of the gas?
A.
B.
C.
D.
-
22M.2.HL.TZ1.9b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
-
22N.1.SL.TZ0.10:
Three statements about Boltzmann’s constant kB are:
I. kB has a unit of J K−1
II. kB
III. kB
Which statements are correct?
A. I and II onlyB. I and III only
C. II and III only
D. I, II and III
-
22N.1.HL.TZ0.11:
Gases in the atmosphere are compounds of , , and .
Four of these gases are CO2, N2O, CH4 and H2O. A pure sample of each gas is produced. Each sample has the same mass.
Which sample contains the greatest number of molecules?
A. N2OB. H2O
C. CO2
D. CH4
- 22N.2.SL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.SL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 22N.2.HL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.HL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 23M.2.HL.TZ2.2a: State the unit for pV in fundamental SI units.
-
23M.1.SL.TZ2.11:
A vessel contains a mass X of helium gas and a mass 2X of oxygen gas.
Molar mass of helium = 4 g
Molar mass of oxygen = 32 g
What is the ?
A.B.
C. 4
D. 8
- 23M.1.SL.TZ2.12: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.SL.TZ2.30: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
-
23M.1.HL.TZ1.25:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
- 23M.2.SL.TZ2.2a: State the unit for pV in fundamental SI units.
-
23M.1.SL.TZ1.29:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.30:
Light of intensity 500 W m−2 is incident on concrete and on snow. 300 W m−2 is reflected from the
concrete and 400 W m−2 is reflected from the snow.What is ?
A.B.
C.
D. 2
- 23M.1.HL.TZ2.9: A fixed mass of an ideal gas expands slowly at constant temperature in a container. Three...
- 23M.1.HL.TZ2.10: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.27: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
-
19M.2.HL.TZ2.2a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.2b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.HL.TZ2.2ci:
Calculate the ratio .
-
19M.2.HL.TZ2.2cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
-
19M.2.HL.TZ2.a:
The mass of a helium atom is 6.6 × 10-27 kg. Estimate the average speed of the helium atoms in the container.
-
19M.2.HL.TZ2.b:
Show that the number of helium atoms in the container is 4 × 1020.
-
19M.2.HL.TZ2.ci:
Calculate the ratio .
-
19M.2.HL.TZ2.cii:
Discuss, by reference to the kinetic model of an ideal gas and the answer to (c)(i), whether the assumption that helium behaves as an ideal gas is justified.
- 19M.2.HL.TZ2.4dii: Suggest, in terms of conservation of energy, the cause for the above change.
- 19M.2.HL.TZ2.dii: Suggest, in terms of conservation of energy, the cause for the above change.
-
19M.1.SL.TZ1.13:
A gas storage tank of fixed volume V contains N molecules of an ideal gas at temperature T. The pressure at kelvin temperature T is 20 MPa. molecules are removed and the temperature changed to 2T. What is the new pressure of the gas?
A. 10 MPa
B. 15 MPa
C. 30 MPa
D. 40 MPa
-
19M.2.SL.TZ1.4a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.4b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.2.SL.TZ1.a:
A solid cylinder of height h and density ρ rests on a flat surface.
Show that the pressure pc exerted by the cylinder on the surface is given by pc = ρgh.
-
19M.2.SL.TZ1.b.i:
Show that (po + pm) × 0.190 = where
po = atmospheric pressure
pm = pressure due to the mercury column
T = temperature of the trapped gas
n = number of moles of the trapped gas
A = cross-sectional area of the tube.
-
19M.1.HL.TZ2.14:
Cylinder X has a volume and contains 3.0 mol of an ideal gas. Cylinder Y has a volume and contains 2.0 mol of the same gas.
The gases in X and Y are at the same temperature . The containers are joined by a valve which is opened so that the temperatures do not change.
What is the change in pressure in X?
A.
B.
C.
D.
-
19M.1.SL.TZ2.12:
A container holds 20 g of argon-40() and 40 g of neon-20 () .
What is in the container?
A. 0.25
B. 0.5
C. 2
D. 4
-
19M.1.SL.TZ2.11:
The temperature of a fixed mass of an ideal gas changes from 200 °C to 400 °C.
What is ?
A. 0.50
B. 0.70
C. 1.4
D. 2.0
-
19M.2.SL.TZ2.2a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.2b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.2c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19M.2.SL.TZ2.2di:
Calculate the ratio .
-
19M.2.SL.TZ2.2dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
-
19M.2.SL.TZ2.a:
The molar mass of helium is 4.0 g mol-1. Show that the mass of a helium atom is 6.6 × 10-27 kg.
-
19M.2.SL.TZ2.b:
Estimate the average speed of the helium atoms in the container.
-
19M.2.SL.TZ2.c:
Show that the number of helium atoms in the container is about 4 × 1020.
-
19M.2.SL.TZ2.di:
Calculate the ratio .
-
19M.2.SL.TZ2.dii:
Explain, using your answer to (d)(i) and with reference to the kinetic model, why this sample of helium can be assumed to be an ideal gas.
- 19N.1.SL.TZ0.10: An ideal gas is in a closed container. Which changes to its volume and temperature when taken...
-
19N.1.SL.TZ0.11:
Two flasks P and Q contain an ideal gas and are connected with a tube of negligible volume compared to that of the flasks. The volume of P is twice the volume of Q.
P is held at a temperature of 200 K and Q is held at a temperature of 400 K.
What is mass of ?
A.
B.
C. 4
D. 8
- 19N.1.HL.TZ0.9: Under which conditions of pressure and density will a real gas approximate to an ideal gas?
-
19N.2.SL.TZ0.2a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
19N.2.SL.TZ0.2b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.2b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
-
19N.2.SL.TZ0.a:
With the door open the air in the refrigerator is initially at the same temperature and pressure as the air in the kitchen. Calculate the number of molecules of air in the refrigerator.
-
19N.2.SL.TZ0.b(i):
Determine the pressure of the air inside the refrigerator.
-
19N.2.SL.TZ0.b(ii):
The door of the refrigerator has an area of 0.72 m2. Show that the minimum force needed to open the refrigerator door is about 4 kN.
- 20N.1.SL.TZ0.11: An ideal gas of constant mass is heated in a container of constant volume. What is the reason...
-
20N.1.SL.TZ0.12:
A substance in the gas state has a density about times less than when it is in the liquid state. The diameter of a molecule is . What is the best estimate of the average distance between molecules in the gas state?
A.
B.
C.
D.
- 20N.1.HL.TZ0.7: What is not an assumption of the kinetic model of an ideal gas? A. Attractive forces between...
-
20N.1.HL.TZ0.9:
Two containers X and Y are maintained at the same temperature. X has volume and Y has volume . They both hold an ideal gas. The pressure in X is and the pressure in Y is . The containers are then joined by a tube of negligible volume. What is the final pressure in the containers?
A.
B.
C.
D.
-
21M.2.SL.TZ1.3a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
- 21M.2.SL.TZ1.3a.ii: State one assumption of the kinetic model of an ideal gas.
-
21M.2.SL.TZ1.a.i:
The molar mass of water is 18 g mol−1. Estimate the average speed of the water molecules in the vapor produced. Assume the vapor behaves as an ideal gas.
- 21M.2.SL.TZ1.a.ii: State one assumption of the kinetic model of an ideal gas.
-
21M.2.SL.TZ2.2a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.2b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.2c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
-
21M.2.SL.TZ2.a:
Deduce whether helium behaves as an ideal gas over the temperature range 250 K to 500 K.
-
21M.2.SL.TZ2.b:
Helium has a molar mass of 4.0 g. Calculate the mass of gas in the container.
-
21M.2.SL.TZ2.c:
A second container, of the same volume as the original container, contains twice as many helium atoms. The graph of the variation of P with T is determined for the gas in the second container.
Predict how the graph for the second container will differ from the graph for the first container.
- 21M.1.SL.TZ1.10: Which aspect of thermal physics is best explained by the molecular kinetic model? A. The...
- 21M.1.HL.TZ1.10: Two ideal gases X and Y are at the same temperature. The mass of a particle of gas X is larger...
- 21M.1.SL.TZ1.25: What is the relation between the value of the unified atomic mass unit in grams and the value of...
- 21M.1.SL.TZ1.12: A quantity of 2.00 mol of an ideal gas is maintained at a temperature of 127 ºC in a container of...
-
21M.1.SL.TZ2.10:
A sample of oxygen gas with a volume of is at . The gas is heated so that it expands at a constant pressure to a final volume of . What is the final temperature of the gas?
A.
B.
C.
D.
-
21M.1.SL.TZ2.11:
Two identical containers X and Y each contain an ideal gas. X has N molecules of gas at an absolute temperature of T and Y has 3N molecules of gas at an absolute temperature of What is the ratio of the pressures ?
A.
B.
C.
D.
-
21N.1.SL.TZ0.12:
A fixed mass of an ideal gas has a volume of , a pressure of p and a temperature of . The gas is compressed to the volume of and its pressure increases to 12p. What is the new temperature of the gas?
A.B.
C.
D.
-
21N.1.HL.TZ0.10:
The molar mass of an ideal gas is . A fixed mass of the gas expands at a constant pressure . The graph shows the variation with temperature T of the gas volume V.
What is the gradient of the graph?
A.B.
C.
D.
-
21N.2.SL.TZ0.2b.i:
Calculate the pressure of the gas.
-
21N.2.SL.TZ0.2b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.SL.TZ0.2c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.SL.TZ0.b.i:
Calculate the pressure of the gas.
-
21N.2.SL.TZ0.b.ii:
The temperature of the gas is increased to 500 K. Sketch, on the axes, a graph to show the variation with temperature T of the pressure P of the gas during this change.
-
21N.2.SL.TZ0.c:
A container is filled with 1 mole of helium (molar mass 4 g mol−1) and 1 mole of neon (molar mass 20 g mol−1). Compare the average kinetic energy of helium atoms to that of neon atoms.
-
21N.2.HL.TZ0.6d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
21N.2.HL.TZ0.d.ii:
Estimate the root mean square speed of nitrogen molecules in the Titan atmosphere. Assume an atmosphere temperature of 90 K.
-
22M.1.SL.TZ2.10:
A quantity of an ideal gas is at a temperature T in a cylinder with a movable piston that traps a length L of the gas. The piston is moved so that the length of the trapped gas is reduced to and the pressure of the gas doubles.
What is the temperature of the gas at the end of the change?
A.
B.
C.
D. - 22M.1.SL.TZ2.11: What is true for an ideal gas? A. nRT = NkBT B. nRT = kBT C. RT = NkBT D. RT = kBT
- 22M.1.SL.TZ2.12: Which assumption is part of the molecular kinetic model of ideal gases? A. The work done on a...
-
22M.2.SL.TZ2.2a:
Calculate the number of gas particles in the cylinder.
- 22M.2.SL.TZ2.2b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.2b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
-
22M.2.SL.TZ2.a:
Calculate the number of gas particles in the cylinder.
- 22M.2.SL.TZ2.b.i: Discuss, for this process, the changes that occur in the density of the gas.
- 22M.2.SL.TZ2.b.ii: Discuss, for this process, the changes that occur in the internal energy of the gas.
-
22M.1.SL.TZ1.12:
An ideal gas is maintained at a temperature of 100 K. The variation of the pressure P and of the gas is shown.
What is the quantity of the gas?
A.
B.
C.
D.
-
22M.2.HL.TZ1.9b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
-
22M.2.HL.TZ1.b.i:
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
-
22N.1.SL.TZ0.10:
Three statements about Boltzmann’s constant kB are:
I. kB has a unit of J K−1
II. kB
III. kB
Which statements are correct?
A. I and II onlyB. I and III only
C. II and III only
D. I, II and III
-
22N.1.HL.TZ0.11:
Gases in the atmosphere are compounds of , , and .
Four of these gases are CO2, N2O, CH4 and H2O. A pure sample of each gas is produced. Each sample has the same mass.
Which sample contains the greatest number of molecules?
A. N2OB. H2O
C. CO2
D. CH4
- 22N.2.SL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.SL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 22N.2.SL.TZ0.b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.SL.TZ0.b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 22N.2.HL.TZ0.2b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.HL.TZ0.2b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 22N.2.HL.TZ0.b.i: State one way in which a real gas differs from an ideal gas.
-
22N.2.HL.TZ0.b.ii:
The water is heated. Explain why the quantity of air in the storage tank decreases.
- 17N.1.SL.TZ0.9: What does the constant n represent in the equation of state for an ideal gas pV = nRT? A. The...
- 17N.1.SL.TZ0.11: Under what conditions of pressure and temperature does a real gas approximate to an ideal gas?
-
17N.1.HL.TZ0.12:
Unpolarized light of intensity I0 is incident on a polarizing filter. Light from this filter is incident on a second filter, which has its axis of polarization at 30˚ to that of the first filter.
The value of cos 30˚ is . What is the intensity of the light emerging through the second filter?
A. I0
B. I0
C. I0
D. I0
- 23M.2.HL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.HL.TZ2.a: State the unit for pV in fundamental SI units.
-
23M.1.SL.TZ2.11:
A vessel contains a mass X of helium gas and a mass 2X of oxygen gas.
Molar mass of helium = 4 g
Molar mass of oxygen = 32 g
What is the ?
A.B.
C. 4
D. 8
- 23M.1.SL.TZ2.12: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.SL.TZ2.30: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
-
23M.1.HL.TZ1.25:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
- 23M.2.SL.TZ2.2a: State the unit for pV in fundamental SI units.
- 23M.2.SL.TZ2.a: State the unit for pV in fundamental SI units.
-
23M.1.SL.TZ1.29:
Two surfaces X and Y emit radiation of the same surface intensity. X emits a radiation of peak wavelength twice that of Y.
What is ?
A.B.
C. 2
D. 16
-
23M.1.SL.TZ1.30:
Light of intensity 500 W m−2 is incident on concrete and on snow. 300 W m−2 is reflected from the
concrete and 400 W m−2 is reflected from the snow.What is ?
A.B.
C.
D. 2
- 23M.1.HL.TZ2.9: A fixed mass of an ideal gas expands slowly at constant temperature in a container. Three...
- 23M.1.HL.TZ2.10: A balloon of volume V contains 10 mg of an ideal gas at a pressure P. An additional mass of the...
- 23M.1.HL.TZ2.27: A planet has an albedo of 0.30. A simplified energy balance for the planet is shown. What is the...
- 18M.1.SL.TZ1.10: A fixed mass of an ideal gas is trapped in a cylinder of constant volume and its temperature is...
-
18M.1.SL.TZ1.12:
A sealed cylinder of length l and cross-sectional area A contains N molecules of an ideal gas at kelvin temperature T.

What is the force acting on the area of the cylinder marked A due to the gas?
A.
B.
C.
D.
-
18M.2.SL.TZ1.2a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.2b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ1.a:
Calculate the pressure of the gas.
-
18M.2.SL.TZ1.b.ii:
Calculate the average kinetic energy of the particles of the gas.
-
18M.2.SL.TZ1.c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.SL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.SL.TZ2.a.i:
State what is meant by an ideal gas.
-
18M.2.SL.TZ2.a.ii:
Calculate the number of atoms in the gas.
-
18M.2.SL.TZ2.a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.SL.TZ2.b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.SL.TZ2.b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ1.2b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.2.HL.TZ1.2c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.2.HL.TZ1.b.ii:
Determine, in kJ, the total kinetic energy of the particles of the gas.
-
18M.2.HL.TZ1.c:
Explain, with reference to the kinetic model of an ideal gas, how an increase in temperature of the gas leads to an increase in pressure.
-
18M.1.HL.TZ2.9:
Q and R are two rigid containers of volume 3V and V respectively containing molecules of the same ideal gas initially at the same temperature. The gas pressures in Q and R are p and 3p respectively. The containers are connected through a valve of negligible volume that is initially closed.

The valve is opened in such a way that the temperature of the gases does not change. What is the change of pressure in Q?
A. +p
B.
C.
D. –p
-
18M.2.HL.TZ2.2a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.2a.ii:
Calculate the number of atoms in the gas.
-
18M.2.HL.TZ2.2a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ2.2b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.2b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18M.2.HL.TZ2.a.i:
State what is meant by an ideal gas.
-
18M.2.HL.TZ2.a.ii:
Calculate the number of atoms in the gas.
-
18M.2.HL.TZ2.a.iii:
Calculate, in J, the internal energy of the gas.
-
18M.2.HL.TZ2.b.i:
Calculate, in Pa, the new pressure of the gas.
-
18M.2.HL.TZ2.b.ii:
Explain, in terms of molecular motion, this change in pressure.
-
18N.1.SL.TZ0.11:
A container is filled with a mixture of helium and oxygen at the same temperature. The molar mass of helium is 4 g mol–1 and that of oxygen is 32 g mol–1.
What is the ratio ?
A.
B.
C.
D. 8
-
18N.1.SL.TZ0.12:
Container X contains 1.0 mol of an ideal gas. Container Y contains 2.0 mol of the ideal gas. Y has four times the volume of X. The pressure in X is twice that in Y.
What is ?
A.
B.
C. 1
D. 2
-
18N.2.SL.TZ0.7b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
- 18N.2.SL.TZ0.7c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
-
18N.2.SL.TZ0.b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of 260 K.
- 18N.2.SL.TZ0.c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
-
18N.2.HL.TZ0.9b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
- 18N.2.HL.TZ0.9c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
-
18N.2.HL.TZ0.b.ii:
Calculate the volume of the oxygen produced in one second when it is allowed to expand to a pressure of 0.11 MPa and to reach a temperature of –13 °C.
- 18N.2.HL.TZ0.c: State one assumption of the kinetic model of an ideal gas that does not apply to oxygen.
