1.9.2 Forms of Complex Numbers

Modulus-Argument (Polar) Form

How do I write a complex number in modulus-argument (polar) form?

The Cartesian form of a complex number, $z = x + i y$ , is written in terms of its real part, $x$ , and its imaginary part, $y$
If we let $r = | z |$ and $θ = \arg z$ , then it is possible to write a complex number in terms of its modulus, $r$ , and its argument, $θ$ , called the modulus-argument (polar) form, given by...
- $z = r (\cos θ + isin θ)$
- This is often written as z = r cis θ
- This is given in the formula book under Modulus-argument (polar) form and exponential (Euler) form
It is usual to give arguments in the range $- π < θ \leq π$ or $0 \leq θ < 2 π$
- Negative arguments should be shown clearly
- e.g. $z = 2 (\cos (- \frac{π}{3}) + isin (- \frac{π}{3})) = 2 cis (- \frac{π}{3})$
  - without simplifying $\cos (- \frac{π}{3})$ to either $\cos (\frac{π}{3})$ or $\frac{1}{2}$
The complex conjugate of r cis θ is r cis (-θ )
If a complex number is given in the form $z = r (\cos θ - isin θ)$ , then it is not in modulus-argument (polar) form due to the minus sign
- It can be converted by considering transformations of trigonometric functions
  - $- \sin θ = \sin (- θ)$ and $\cos θ = \cos (- θ)$
- So $z = r (\cos θ - isin θ) = z = r (\cos (- θ) + isin (- θ)) = r cis (- θ)$
To convert from modulus-argument (polar) form back to Cartesian form, evaluate the real and imaginary parts
- E.g. $z = 2 (\cos (- \frac{π}{3}) + isin (- \frac{π}{3}))$ becomes $z = 2 (\frac{1}{2} + i (- \frac{\sqrt{3}}{2})) = 1 - \sqrt{3} i$

How do I multiply complex numbers in modulus-argument (polar) form?

The main benefit of writing complex numbers in modulus-argument (polar) form is that they multiply and divide very easily
To multiply two complex numbers in modulus-argument (polar) form we multiply their moduli and add their arguments
- $|z_{1} z_{2}| = |z_{1}| |z_{2}|$
- $\arg (z_{1} z_{2}) = \arg z_{1} + \arg z_{2}$
So if z₁ = r₁ cis (θ₁) and z₂ = r₂ cis (θ₂)
- z₁ z₂= r₁r₂ cis (θ₁ + θ₂)
Sometimes the new argument, $θ_{1} + θ_{2}$ , does not lie in the range $- π < θ \leq π$ (or $0 \leq θ < 2 π$ if this is being used)
- An out-of-range argument can be adjusted by either adding or subtracting $2 π$
- E.g. If $θ_{1} = \frac{2 π}{3}$ and $θ_{2} = \frac{π}{2}$ then $θ_{1} + θ_{2} = \frac{7 π}{6}$
- This is currently not in the range $- π < θ \leq π$
- Subtracting $2 π$ from $\frac{7 π}{6}$ to give $- \frac{5 π}{6}$ , a new argument is formed
  - This lies in the correct range and represents the same angle on an Argand diagram
The rules of multiplying the moduli and adding the arguments can also be applied when…
- …multiplying three complex numbers together, $z_{1} z_{2} z_{3}$ , or more
- …finding powers of a complex number (e.g. $z^{2}$ can be written as $z z$ )
The rules for multiplication can be proved algebraically by multiplying z₁ = r₁ cis (θ₁) by z₂ = r₂ cis (θ₂), expanding the brackets and using compound angle formulae

How do I divide complex numbers in modulus-argument (polar) form?

To divide two complex numbers in modulus-argument (polar) form, we divide their moduli and subtract their arguments
- $|\frac{z_{1}}{z_{2}}| = \frac{|z_{1}|}{| z_{2} |}$
- $\arg (\frac{z_{1}}{z_{2}}) = \arg z_{1} - \arg z_{2}$
So if z₁ = r₁ cis (θ₁) and z₂ = r₂ cis (θ₂) then
- $\frac{z_{1}}{z_{2}} = \frac{r_{1}}{r_{2}} cis (θ_{1} - θ_{2})$
Sometimes the new argument, $θ_{1} - θ_{2}$ , can lie out of the range $- π < θ \leq π$ (or the range $0 < θ \leq 2 π$ if this is being used)
- You can add or subtract $2 π$ to bring out-of-range arguments back in range
The rules for division can be proved algebraically by dividing z₁ = r₁ cis (θ₁) by z₂ = r₂ cis (θ₂) using complex division and the compound angle formulae

Exam Tip

Remember that r cis θ only refers to $r (\cos θ + isin θ)$
- If you see a complex number written in the form $z = r (\cos θ - isin θ)$ then you will need to convert it to the correct form first
- Make sure you are confident with basic trig identities to help you do this

Worked Example

Let $z_{1} = 4 \sqrt{2} cis \frac{3 π}{4}$ and $z_{2} = \sqrt{8} (\cos (\frac{π}{2}) - isin (\frac{π}{2}))$

Find

z_{1} z_{2}

, giving your answer in the form

r (\cos θ + isin θ)

where

0 \leq θ < 2 π

1-9-2-ib-aa-hl-forms-of-cn-we-solution-1-a

Find

\frac{z_{1}}{z_{2}}

, giving your answer in the form

r (\cos θ + isin θ)

where

- π \leq θ < π

1-9-2-ib-aa-hl-forms-of-cn-we-solution-1-b

Exponential (Euler's) Form

How do we write a complex number in Euler's (exponential) form?

A complex number can be written in Euler's form as $z = r e^{i θ}$

This relates to the modulus-argument (polar) form as $z = r e^{i θ} = r cis θ$
This shows a clear link between exponential functions and trigonometric functions
This is given in the formula booklet under 'Modulus-argument (polar) form and exponential (Euler) form'

The argument is normally given in the range 0 ≤ θ < 2π

However in exponential form other arguments can be used and the same convention of adding or subtracting 2π can be applied

How do we multiply and divide complex numbers in Euler's form?

Euler's form allows for quick and easy multiplication and division of complex numbers
If $z_{1} = r_{1} e^{i θ_{1}}$ and $z_{2} = r_{2} e^{i θ_{2}}$ then
- $z_{1} \times z_{2} = r_{1} r_{2} e^{i (θ_{1} + θ_{2})}$
  - Multiply the moduli and add the arguments
- $\frac{z_{1}}{z_{2}} = \frac{r_{1}}{r_{2}} e^{i (θ_{1} - θ_{2})}$
  - Divide the moduli and subtract the arguments
Using these rules makes multiplying and dividing more than two complex numbers much easier than in Cartesian form
When a complex number is written in Euler's form it is easy to raise that complex number to a power
- If $z = r e^{i θ}$ , $z^{2} = r^{2} e^{2 i θ}$ and $z^{n} = r^{n} e^{ni θ}$

What are some common numbers in exponential form?

As $\cos (2 π) = 1$ and $\sin (2 π) = 0$ you can write:
- $1 = e^{2 π i}$
Using the same idea you can write:
- $1 = e^{0} = e^{2 π i} = e^{4 π i} = e^{6 π i} = e^{2 k π i}$
- where k is any integer
As $\cos (π) = - 1$ and $\sin (π) = 0$ you can write:
- $e^{π i} = - 1$
- Or more commonly written as $e^{iπ} + 1 = 0$
  - This is known as Euler's identity and is considered by some mathematicians as the most beautiful equation
As $\cos (\frac{π}{2}) = 0$ and $\sin (\frac{π}{2}) = 1$ you can write:
- $i = e^{\frac{π}{2} i}$

Exam Tip

Euler's form allows for easy manipulation of complex numbers, in an exam it is often worth the time converting a complex number into Euler's form if further calculations need to be carried out
- Familiarise yourself with which calculations are easier in which form, for example multiplication and division are easiest in Euler's form but adding and subtracting are easiest in Cartesian form

Worked Example

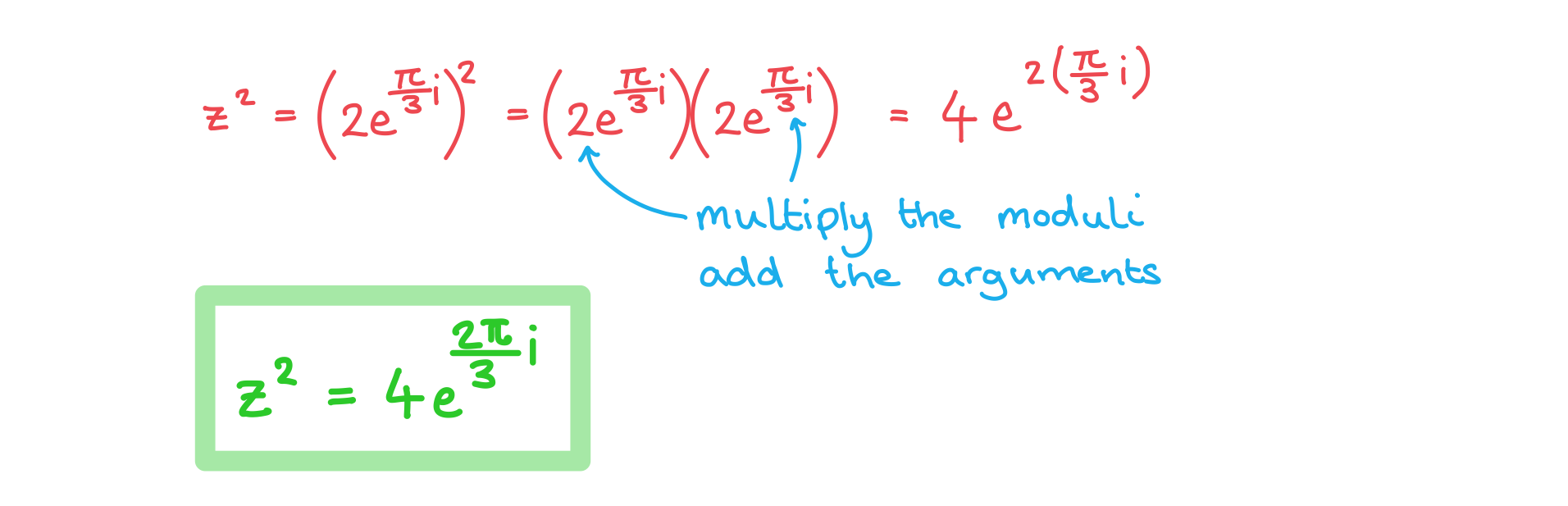
Consider the complex number $z = 2 e^{\frac{π}{3} i}$ . Calculate $z^{2}$ giving your answer in the form $r e^{i θ} .$

1-9-2-ib-aa-hl-forms-of-cn-we-solution-2-eulers

Conversion of Forms

Converting from Cartesian form to modulus-argument (polar) form or exponential (Euler's) form.

To convert from Cartesian form to modulus-argument (polar) form or exponential (Euler) form use
- $r = |z| = \sqrt{x^{2} + y^{2}}$
and
- $θ = \arg z$

Converting from modulus-argument (polar) form or exponential (Euler's) form to Cartesian form.

To convert from modulus-argument (polar) form to Cartesian form

Write z = r (cosθ + isinθ ) as z = r cosθ + (r sinθ )i
Find the values of the trigonometric ratios r sinθ and r cosθ

You may need to use your knowledge of trig exact values

Rewrite as z = a + bi where

a = r cosθ and b = r sinθ

To convert from exponential (Euler’s) form to Cartesian form first rewrite z = r e^iθ in the form z = r cosθ + (r sinθ)i and then follow the steps above

Exam Tip

When converting from Cartesian form into Polar or Euler's form, always leave your modulus and argument as an exact value
- Rounding values too early may result in inaccuracies later on

Worked Example

Two complex numbers are given by $z_{1} = 2 + 2 i$ and $z_{2} = 3 e^{\frac{2 π}{3} i}$ .

Write

z_{1}

in the form

r e^{i θ}

1-9-2-ib-aa-hl-forms-of-cn-we-solution-3-a

Write

z_{2}

in the form

r (\cos θ + isin θ)

and then convert it to Cartesian form.

1-9-2-ib-aa-hl-forms-of-cn-we-solution-3-b

DP IB Maths: AA HL

Revision Notes

1.9.2 Forms of Complex Numbers

Modulus-Argument (Polar) Form

How do I write a complex number in modulus-argument (polar) form?

How do I multiply complex numbers in modulus-argument (polar) form?

How do I divide complex numbers in modulus-argument (polar) form?

Exam Tip

Worked Example

Exponential (Euler's) Form

How do we write a complex number in Euler's (exponential) form?

How do we multiply and divide complex numbers in Euler's form?

What are some common numbers in exponential form?

Exam Tip

Worked Example

Conversion of Forms

Converting from Cartesian form to modulus-argument (polar) form or exponential (Euler's) form.

Converting from modulus-argument (polar) form or exponential (Euler's) form to Cartesian form.

Exam Tip

Worked Example

Author: Amber

Resources

Members

Company

Quick Links