A.8 Superconducting metals & X-ray crystallography
Written specifically for students to provide help and support for the IB Diploma chemistry programme this page provides full coverage of the syllabus content of Option A - sub topic A.8. It encourages you to think critically and provides many questions with full worked answers so that you can monitor and improve your knowledge and understanding.
.png)
 Learning outcomes
Learning outcomes
After studying this topic you should be able to:
.png) Understand:
Understand:
- Materials that offer no resistance to electric currents below a critical temperature are known as superconductors.
- The Meissner effect relates to the ability of a superconductor to create a magnetic field that is a mirror image of an external field, thus expelling it.
- Metallic conductors have electrical resistance due to the collisions between electrons and the positive ions of the lattice.
- Bardeen–Cooper–Schrieffer (BCS) theory explains that electrons in superconductors that are below the critical temperature form Cooper pairs that are able to move freely through the superconductor.
- Superconductors can be categorized into two types. In type 1 superconductors there is a sharp transition to superconductivity whereas the transition is more gradual in type 2 superconductors.
- Structures of metallic and ionic compounds can be analysed by X-ray diffraction.
- Crystal lattices contain simple repeating unit cells.
- The atoms on faces and edges of unit cells are shared between adjacent unit cells.
- The coordination number refers to the number of nearest neighbours of an atom or ion.
Apply your knowledge to:
- Analyse resistance versus temperature data for type 1 and type 2 superconductors.
- Explain superconductivity in terms of Cooper pairs moving through a positive ion lattice.
- Deduce or construct unit cell structures from crystal structure information.
- Apply the Bragg equation, nλ = 2dsinθ, in metallic structures.
- Determine the density of a pure metal from its atomic radii and crystal packing structure.
Relationships & vocabulary
Nature of science
The discovery that superconducting materials have zero electrical resistance below a certain temperature, provides a good example of how theories need to be modified to fit new data.
This sub-topic also illustrates the importance of understanding the basic scientific principles behind modern instrumentation.
International-mindedness
Advanced analytical techniques have many applications (e.g. in forensics, mineral exploration, medicine etc.) It is worth considering how world economies are affected by unequal access to these advanced techniques.
Vocabulary
| superconductor/superconductivity | type 1 & type 2 superconductors | Cooper pair | Meissner effect |
| Bardeen–Cooper–Schrieffer (BCS) theory | X-ray diffraction | Bragg equation | unit cell |
| simple cubic cell | face-centred cubic (FCC) | body centred cubic (BCC) | perovskite structure |
Learning slides
You can use this slide gallery for learning or for reviewing concepts and information. It covers all the key points in the syllabus for this sub-topic.
Something to think about
In JIB Docs (2) Teamary 2017 yet another revised version of the data booklet became available. However there is still a real problem with the atomic radii given for the elements in Groups 1, 2 and 13.
The images below show how the values for Groups 1 and 2 have changed from the data booklet used for the previous programme.
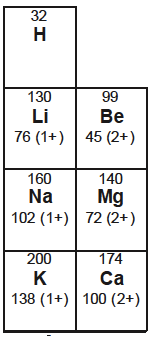
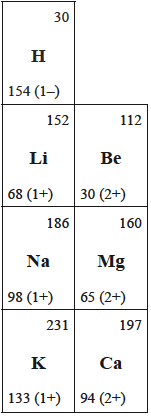
The table on the left is from Section 9 of the current 2016 data booklet whereas the table on the right is from Table 8 of the 2009 data booklet. Both give the atomic and ionic radii when multiplied by 1 x 10−12 m.
‘Under the Applications and skills’ section for this sub-topic it states “Determination of the density of a pure metal from its atomic radii and crystal packing structure”.
Consider the following problem that could easily be set by the IB to cover this area.
Sodium forms a body-centred cubic unit cell. That is, the atoms occupy 68% of the available space. Determine the density of sodium.
To solve this problem we would use the 2016 data booklet (latest version updated in JIB Docs (2) Teamary 2017) to find that the radius of one sodium atom is 1.60 x 10-10 m. We would then find the volume of one atom and hence the volume of one mole of sodium atoms. Knowing that the packing is only 68% efficient we could find the actual volume of a lattice containing one mole of sodium atoms. We know from Section 6 in the data booklet that this has a mass of 22.99 g mol-1 so we can then determine the density by dividing the mass by the volume.
The volume of one sodium atom = 4/3 πr3
= 4/3 x 3.14 x (1.60 x 10-10)3 = 1.715 x 10-29 m3
The volume of one mole of sodium atoms
= 1.715 x 10-29 x 6.02 x 1023 = 1.032 x 10-5 m3
The volume of a lattice containing one mole of sodium atoms
= 100/68 x 1.032 x 10-5 = 1.518 x 10-5 m3
The density of sodium (knowing that the atomic mass of sodium is 22.99 g mol-1)
= 22.99 / (1.518 x 10-5) = 1.51 x 106 g m-3 = 1.51 g cm-3
There is a serious problem with this answer. You should realise that it cannot possibly be correct as sodium floats on water so it has a density of less than 1 g cm-3.
In fact the density of sodium is 0.968 g cm-3 (or 9.68 x 105 g m-3)
What happens if we use this value and work backwards to find the radius of a sodium atom?
Volume of lattice containing one mole
= 22.99 / (9.68 x 105) = 2.38 x 10-5 m3
Volume of one mole of sodium atoms
= 68/100 x 2.38 x 10-5 = 1.62 x 10-5 m3
Volume of one sodium atom
= 1.62 x 10-5 / 6.02 x 1023 = 2.69 x 10-29 m3
(Radius of a sodium atom)3 = 2.69 x 10-29 x ¾ x 1/3.14 = 6.43 x 10-30 m3
Radius of one sodium atom
= (6.43 x 10-30)⅓ = 1.86 x 10-10 m = 186 x 10-12 m
Surprise surprise. Where have we seen this value before? It is the value given in the old data booklet (see above) that used the value for the metallic radius for sodium (and the other metals). I do wonder why all the values were changed and whether anyone gave any serious thought to it. The new values, which give the covalent radii rather than the metallic radii, have the potential to cause considerable problems in the examinations on the current programme when the data booklet (for first exams in 2016) must be used.
Test your understanding of this topic
(Note that your teacher may have restricted your access to some or all of these questions and worked answers if they are going to use them as a class test or set them as an assignment.)
For ten 'quiz' questions (for quick testing of knowledge and understanding with the answers explained) see MC test: Superconducting metals & X-ray crystallography.
For short-answer questions see Superconducting metals & X-ray crystallography questions together with the worked answers on a separate page Superconducting metals & X-ray crystallography answers.
More resources
1. An explanation of superconductivity at about the right level (it is actually for British A level Physics).
2. A very neat demonstration of the Meissner effect - although unfortunately the sound explanation is not present.
3. Richard Thornley applies the Bragg equation. However remember that although the theory is fine the radii used from the data booklet are the covalent radii not the metallic radii so some of values are not correct (see 'Something to think about' above).

 IB Docs (2) Team
IB Docs (2) Team 






















