DP Chemistry: Nuclear fusion & fission (HL)
Teacher only page

Nuclear fusion & fission (HL)

C.7 Nuclear fusion & nuclear fission (HL) (3 hours)

Pause for thought

Who sets the trends?

Under ‘Applications and skills’ the syllabus asks for a discussion on the different properties of uranium dioxide, UO2, and uranium hexafluoride, UF6, in terms of structure and bonding. This is fine and necessary as uranium dioxide is used as a nuclear fuel whereas uranium hexafluoride is used for enrichment. Uranium dioxide has a calcite (CaF2) ionic crystalline structure with each uranium atom surrounded by 8 oxygen atoms. This gives it a high melting point of 2865 oC. Uranium hexafluoride is covalent with weak intermolecular forces between the octahedral UF6 molecules, which means its melting point is much lower. In fact it sublimes when heated as its boiling point is 56.5 oC and its melting point is 64.5 oC.

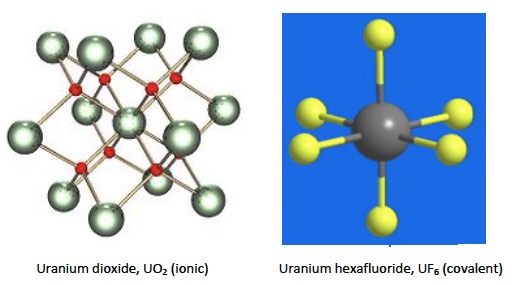
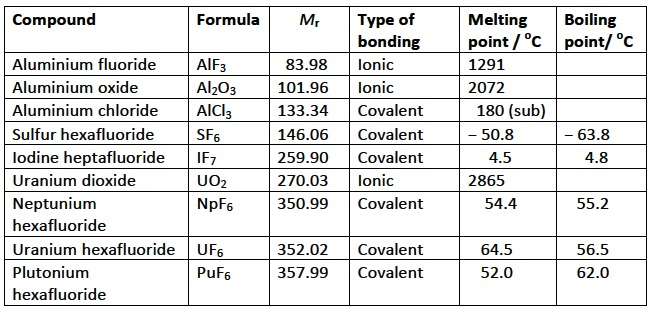
The problem I have is with the Nature of Science statement. This states that the intermolecular forces in uranium hexafluoride are anomalous and do not follow the normal trends – this is given as an example of a discrepancy in trends. To me this statement seems to have been made rather in ignorance, i.e. using only a limited knowledge of chemistry upon which to base the ‘normal’ trend. If you take the oxides and fluorides of aluminium, Al2O3 and AlF3 then both are ionic and have high melting points (Al2O3 melts at 2027 oC and AlF3 melts at 1291 oC). This is basic school chemistry and perhaps the “anomalous” trend for UF6 was based upon this fact, as it would be expected to be ionic? However, even with a basic knowledge of school chemistry it should be known that higher fluorides cannot be ionic as metals rarely form more than a 3+ ion as the charge density becomes too high. Even aluminium chloride is covalent and sublimes at 180 oC. Other higher fluorides mentioned in school chemistry syllabi include sulfur hexafluoride, SF6, and iodine heptafluoride, IF7. Both of these are gases at room temperature, even though they have quite high relative molar masses. To me the fact that uranium hexafluoride has a low melting point and boiling point is not surprising at all – it is just following the expected trend for higher fluorides. If you look at the table below, far from UF6 being anomalous the trend is also followed for the hexafluorides of plutonium and neptunium too. If you are still not convinced and want to use the van Arkel-Ketelaar diagram to support your view, then look at question 3 in the Materials science introduction questions.

Nature of science

The understanding of nuclear processes comes from both theoretical and experimental advances. The anomalous intermolecular forces in uranium hexafluoride, UF6, are given as an example of a discrepancy, as the syllabus claims it does not follow the expected trend.

Learning outcomes

After studying this topic students should be able to:

Understand:

Nuclear fusion:

  • The difference between the mass of the nucleus and the sum of the masses of its individual nucleons is known as the mass defect, Δm.
  • The energy required to separate a nucleus into protons and neutrons is known as the nuclear binding energy, ΔE.

Nuclear fission:

  • Einstein's mass–energy equivalence relationship
    E = mc2 can be used to calculate the energy produced in a fission reaction, where m is equal to the mass difference between the products and reactants and c is the velocity of light.
  • Uranium hexafluoride can be used to separate the different isotopes of uranium for fuel enrichment either by using diffusion or centrifugation.
  • Graham's law states that the rate of effusion of a gas is inversely proportional to the square root of its molar mass.
  • Radioactive decay is a first order process with the half-life, t½, related to the decay constant, λ, by the equation: λ = ln 2 / t½.
  • Nuclear energy is dangerous due to the ionizing nature of the radiation it produces. This can lead to the formation of oxygen free radicals such as superoxide, O2−, and hydroxyl, HO·. These free radicals can initiate chain reactions that can cause damage to DNA and enzymes in living cells.

Apply their knowledge to:

Nuclear fusion:

  • Calculate the mass defect and binding energy of a nucleus.
  • Apply Einstein’s equation E = mc2, to determine the energy produced in a fusion reaction.

Nuclear fission:

  • Apply Einstein’s equation E = mc2, to determine the energy produced in a fission reaction.
  • Discuss the different properties of UO2 and UF6 in terms of bonding and structure.
  • Solve problems involving radioactive half-life, t½.
  • Explain the relationship between Graham’s law of effusion and the kinetic theory of matter.
  • Solve problems on the relative rates of effusion using Graham’s law.

Clarification notes

Students are not expected to recall either specific fission reactions or the workings of nuclear power plants

Safety and risk issues include: health, problems associated with nuclear waste and the possibility that nuclear fuels may be used in nuclear weapons.

Graham’s law of effusion and decay relationships are given in Section 1 of the data booklet.

A binding energy curve can be found in Section 36 of the data booklet.

International-mindedness

Relatively few countries have developed nuclear weapons. The International Atomic Energy Agency (IAEA) works to limit the spread of this technology. Disputes have arisen about whether the nuclear development programmes of some countries are for peaceful or non-peaceful purposes

Nuclear incidents have a global effect. Three Mile Island, Chernobyl and Fukushima-Daiichi could be discussed to illustrate the potential dangers.

Teaching tips

This sub-topic naturally follows on from C.3: Nuclear fusion and nuclear fission. If you are fortunate enough to just be teaching Higher Level students on their own then it makes sense to teach C.3 and this sub-topic as one continuous topic. In fact when covering half-life there seems to be considerable overlap. In C.3 problems involving integral numbers of half-lives are included. These can normally be solved by inspection. In this sub-topic the equations involving λ, the decay constant, are required to solve problems involving non-integral numbers of half-lives Rather strangely, these equations are given in the ‘Guidance’ for C.3 and also are listed in Section 1 as being required for C.3 even though they are not really needed until C.7.

Other than half-life there are two other main concepts to be covered: Einstein’s mass energy equivalence equation and problems involving Graham’s law.

E= mc2 uses the mass defect to solve problems involving binding energy and the energy released in nuclear reactions. Stress to your students that the mass must be in kilograms. When the velocity of light is given in ms-1 then the equivalent energy will be in joules (not kilojoules). It is worth comparing the specific energy of a nuclear fuel with conventional fuels such as coal or gas.

Graham’s law is included in order to explain how uranium can be enriched using uranium hexafluoride. Show how the law can be derived by considering that the temperature of a gas is proportional to the average kinetic energy and distinguish between effusion (through a small hole in the barrier between two volumes) and diffusion (occurs when there are large holes in the barrier, i.e. effectively no barrier at all). Note that centrifugation tends to be used rather than repeated effusion now to enrich uranium.

Study Guide

Pages 150 & 151

Questions

For ten 'quiz' questions (for quick testing of knowledge and understanding with the answers explained) see MC test: Nuclear fusion & nuclear fission (HL).

For short-answer questions see Nuclear fusion & fission reactions (HL) questions together with the worked answers on a separate page Nuclear fusion & fission reactions (HL) answers.

Vocabulary list

mass defect
nuclear binding energy
uranium hexafluoride
effusion
diffusion
centrifugation
Graham's law
radioactive half-life, t½

Teaching slides

Teachers may wish to share these slides with students for learning or for reviewing key concepts.

  

Other resources

1. A DNews video which explains how centrifugation of uranium hexafluoride leads to enriched uranium.

  How uranium is turned into a nuclear fuel

2. A crash course on effusion, diffusion and the velocity of a gas which includes Graham’s law.

  Effusion, diffusion and Graham's law

3. A useful fact sheet on uranium hexafluoride the ‘molecule of the month’ by Simon Cotton, Uppingham School, UK.

All materials on this website are for the exclusive use of teachers and students at subscribing schools for the period of their subscription. Any unauthorised copying or posting of materials on other websites is an infringement of our copyright and could result in your account being blocked and legal action being taken against you.